- Let $f(n)=n^3$ and $g(n)=n^2(\log_2{n})^{12}$. Is $f$ in $O(g)$, $\Omega(g)$, or $\Theta(g)$? What value of $n$ makes $f(n)=g(n)$?
ANSWER:
The former will outrun the latter after some point (because $n$ outruns $(\log{n})^k$ for any $k$), so $f$ = $\Omega(g)$.
As to what value of $n$ makes the two functions equal, you can use a solver that will probably happily announce that $n$ is 2.08977.... But that’ the wrong answer! That is not the $n$ at which $f(n)$ surpasses $g(n)$. That value is much, much, larger, as you can see here:
The query you want to give Wolfram Alpha is “
real roots of n-(log_2(n))^12”. The answers you will get are:- $\approx 0.518789$
- $\approx 2.08977$
- $\approx 3.00405 \times 10^{22}$
The last one is the one you want.
- So you’re reading this fancy paper on algorithms and you see a
small snippet of code. It’s a recursive algorithm, with a small
enough number of recursive calls that you can count them on two hands.
The paper says that complexity of the algorithm is
“obviously $\Theta(n^{2.58496250072})$.” Explain the structure of
the algorithm and how this “obvious”
value was obtained.
ANSWER:
$\Theta(n^{2.58496250072})$ is $\Theta(n^{log_2{6}})$, so the algorithm does divide and conquer by breaking the problem down into 6 pieces — that's 6 recursive calls, countable on two hands — each processing half the amount of the original problem, with the time taking to reassemble the solution being quadratic or less. Saying that this follows directly from the Master Theorem is a good enough answer for the exam.
- One of the freshman tried to do RSA. The student chose $p=87$, $q=73$, and correctly
computed $N=6351$. However, the student forgot to compute $(p-1)(q-1)$ and instead
picked $e=5$ and computed $d$ as the modular inverse of $e$ and $N$. What value of
$d$ arose from this mistake? Show the value that results from
encrypting then decrypting the message $200$, e.g. compute $200^e \bmod N$ then
decrypt the result. If this works, explain why we have to compute $(p-1)(q-1)$ in
“regular” RSA. If not, why don't you get the original message back?
ANSWER:
The student computed $N = pq = 6351$ and $\phi = (p-1)(q-1) = 86 \times 72 = 2192$, and chose $e=5$, and due to inexperience, computed $d$ incorrectly as $d = \mathrm{invmod}(5, 6351) = 5081$. This doesn't work because the message $200$ would be encoded as $\mathrm{powermod}(200,5,6497) = 134$, but decoding it with the erroneous $d$ gives you $\mathrm{powermod}(134,5081,6351) = 6011$. You don't get the original message back because there is absolutely no reason why you would! Thinking that you would get the message back would come from a misunderstanding of modular arithmetic. After all $(m^e \bmod N)^d \bmod N = m^{ed} \bmod N$, but here you cannot take advantage of the fact that $ed \bmod N = 1$. There's no modulo in that exponent!
- Consider the undirected,
weighted graph with vertices $\{A, B, C, D, E, F\}$ and edges
$(A,B,5)$, $(B,D,6)$, $(B,C,1)$, $(A,C,3)$, $(F,E,2)$, $(D,E,2)$, $(E,C,8)$, $(A,E,1)$,
and $(C,D,1)$. Again, please note the graph is undirected.
- Draw the graph.
- Which edges are bridges?
- Which nodes are articulation points?
- Enumerate the nodes in depth-first order, starting at $A$, always choosing the node that comes first in alphabetical order whenver you have a choice.
- Enumerate the nodes in breadth-first order, starting at $A$, always choosing the node that comes first in alphabetical order whenver you have a choice.
ANSWER:
-

- $(E,F)$ is the only bridge
- $E$ is the only articulation point
- Alphabetical DFT: ABCDEF
- Alphabetical BFT: ABCEDF
- For the graph in the previous problem:
- What order are edges added to a MST, using Kruskal's algorithm?
- What order are nodes added to a MST, using Prim's algorithm? Always using alphabetical order whenever you have an arbitrary choice to make.
- What is the shortest path from $B$ to $F$?
- Is there a Hamilton Cycle? If so, name one. If not, why not?
- Is there a Hamilton Path? If so, name one. If not, why not?
- Is there an Euler Trail? If so, name one. If not, why not?
ANSWER:
- Kruskal Addition Order: AE1, BC1, CD1, DE2, EF2
- Prim Addition Order: AEDCBF
- Length 6: $B \rightarrow C \rightarrow D \rightarrow E \rightarrow F$
- No Hamilton Cycles because $F$ has degree = 1
- Hamilton Path: $\langle ABCDEF\rangle$
- No Euler Trail because four nodes have odd degree (not two).
- One of the freshman ran Dijkstra's single-source shortest path algorithm starting
from $A$ on the directed graph with edges $(A,B,7)$, $(A,E,4)$,
$(A,F,5)$, $(F,C,-15)$, $(E,B,1)$, $(C,D,4)$, and $(E,D,2)$. Did the student get the right
answer? What would happen if the edge from $A$ to $F$ were reweighted to 8?
ANSWER:
First, the student gets lucky. Dijkstra's algorithm proceeds as follows:
(A,0) A: 0 (B,7) (E,4) (F,5) E: 4 (B,5) (D,6) (F,5) B: 5 (D,6) (F,5) F: 5 (C,-10) (D,6) C: -10 (D,-6) D: -6
When the link from $A$ to $F$ becomes 8, the algorithm FAILS:
(A,0) A: 0 (B,7) (E,4) (F,8) E: 4 (B,5) (D,6) (F,8) B: 5 (D,6) (F,8) D: 6 <---- NOOOOOOOOOOO! (F,8) F: 8 (C,-7) C: -7 (But D was already chosen! FAIL!!)
- Fill out the bottom-up dynamic programming table for the 0-1
knapsack problem given a 15kg sack and the following items:
- Item A, 2 kg, value = $7.
- Item B, 3 kg, value = $10.
- Item C, 5 kg, value = $18.
- Item D, 6 kg, value = $20.
ANSWER INLINE:
Process them in alphabetical order.0123456789101112131415A 0 0 7 7 7 7 7 7 7 7 7 7 7 7 7 7 A,B 0 0 7 10 10 17 17 17 17 17 17 17 17 17 17 17 A,B,C 0 0 7 10 10 18 18 25 28 28 35 35 35 35 35 35 A,B,C,D 0 0 7 10 10 18 20 25 28 30 35 38 38 45 48 48 - Show the development of the search tree for the top-down
version in the last problem. Mark
the points in the search tree where you would use a pre-computed result.
ANSWER:
If at each step you only consider item with labels lexicographically greater than the item you just looked at, you really never do use a precomputed result. Of course, technically, all the items with smaller labels were precomputed ☺.
Nodes in the tree have the form $c(v)$ where $c$ is the remaining capacity and $v$ is the value of items in the sack so far. We start with the sack empty, that is 15 kilos remaining, and 0 as the value so far. The process goes like this:
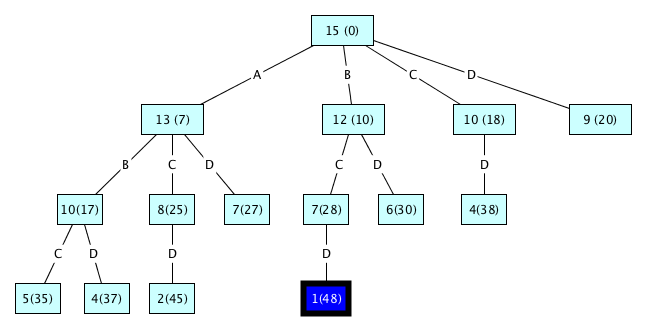
- What graph algorithm is this? Why does it work?
def mystery(g): def helper(n, s): if len(s) == g.order: return True for m in n.adjacent_nodes(): if m not in s: helper(m, s.union({m})) return False for n in g.nodes: if helper(n, {n}): return True return FalseANSWER:
This returns whether or not graph $g$ has a Hamilton Path. The helper method tries to complete a Hamilton Path from node $n$, given that the nodes in $s$ have already been visited. The base case is when all of them have been visited. The main function tries each node as a possible starting point of the path. The algorithm returns as soon as a Hamilton path is found, only returning false after all possible paths have been tried without success.
- An algorithm with complexity function $T(n) = n^4$
can process a 16-element list on our PC in 256 seconds.
- How much time is needed to process a 32-element list?
- If we ran the algorithm on a machine that was 1024 times faster than our PC, how large of a list could we process in one day? (Note 1 day = 86400 seconds)
- If we needed a computer that could process 100 elements in a minute, how much faster than our original PC does this computer need to be?
ANSWER:
Computer speed is $2^{16}/256$ ops/sec = $256$ ops/sec.
- $32^4/256$ = $(2^5)^4/(2^8)$ = $2^{12}$ = 4096 seconds.
- New computer speed = $2^{18}$ ops/sec. So $2^{18} \times 86400 = 22649241600$ ops ⇒ 387 elements.
- $10^8/60/256 \approx$ 6510 times faster.