CMSI 2130: Algorithms Practice Questions

Math
1. Prove that: $a^{\log_b{c}} = c^{\log_b{a}}$
2. Express $(10 \log_2{n})^{\log_{10}{n}}$ in the form $n^{c+f(n)}$ where $c$ is some positive constant. (Hint: Did you do the previous problem?)
3. Solve for $x$. No calculators. Solve exactly, Show your work. $$ 3^{\log_2(\log_5{x})} = \left(\frac{6}{\log_2{5}}\right)^{\log_2{3}} $$
Basic Data Structures
1. The following characters were inserted into an initially empty binary min heap, in this order: Z R S Q P L K I A C. Then two remove_min operations were performed. Show the resulting min-heap.
2. A binary min-heap starts off empty. Show its shape (actually draw the tree) after each of the steps in the following sequence.
  1. Insert 10
  2. Insert 4
  3. Insert 16
  4. Insert 3
  5. Insert 1
  6. Remove
  7. Insert 7
  8. Remove
  9. Remove
  10. Remove
3. What is the height of a (binary) heap with n elements? Give the exact answer. You may have to use floor and ceiling operators. Get it right.
4. Prove that the running time of the standard heapify algorithm, for turning an array, in place, into a heap is $\Theta(n)$, where $n$ is the number of elements in the array.
5. Both stacks and queues are a kind of priority queue. What exactly does this statement mean?
6. Draw the tallest possible red-black tree with 17 nodes.
Complexity
1. What is the time complexity of this code fragment? (Use Θ-notation)
```
int x = 1;
for (int i = 0; i < n; i++) {
    for (int j = 1; j <= x; j++) {
        System.out.println("*");
    }
    x = x + x;
}
```
2. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 0; i < n; i++) {
    for (int j = 0; j < i; i *= 2) {
        System.out.println("*");
    }
}
```
3. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i * i <= n; i++) {
    for (int j = 1; j <= n; j += j) {
        System.out.println("*");
    }
}
```
4. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i <= n; i *= 2)
    for (int j = 1; j <= n; j++)
        System.out.println("*");
    }
}
```
5. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i <= n; i *= 2)
    for (int j = 1; j <= i; j++)
        System.out.println("*");
    }
}
```
6. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i <= n * n; i++) {
    for (int j = 1; j <= n; j *= 2) {
        System.out.println("*");
    }
}
```
7. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i * i; j *= 2) {
        System.out.println("*");
    }
}
```
8. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j *= 2) {
        System.out.println("*");
    }
}
```
9. What is the time complexity of this code fragment? (Use Θ-notation)
```
for (int i = n; n >= 1; n /= 4) {
    for (int j = 0; j < i; j++) {
        System.out.println("*");
    }
}
```
10. Give both the best-case and worst-case time complexities of this function. (Use Θ-notation)
```
public static long power(int x, int n) {
    return n == 0 ? 1
        : n % 2 == 0 ? power(x * x, n / 2)
        : x * power(x * x, n / 2)
}
```
11. Give both the best-case and worst-case time complexities of this function. (Use Θ-notation)
```
public static long power(int x, int n) {
    return n == 0 ? 1
        : n % 2 == 0 ? power(x * x, n / 2)
        : x * power(x * x, n / 2)
}
```
12. What is the time complexity (in Θ-notation) of a procedure to print out the exact value of $2^n$, where $n$ is a nonnegative integer? The procedure described is supposed to print a result no matter how large the result may be.
13. An algorithm with time complexity $T(n) = n^3$ can process a 100-element list on our PC in 10 seconds.
  1. How long would it take to process a 200-element list?
  2. If we ran the algorithm on a machine that was 10 times faster than our PC, how large of a list could we process in 30 seconds?
  3. How much faster than our PC would a computer have to be in order to process a 1000000000-element list in a time span of 1 hour?
14. An algorithm with complexity function $T(n) = n \log{n}$ processes a 64-element list in three minutes and 12 seconds on our PC.
  1. How long does it take to process a 128-element list?
  2. How large of a list could a computer that is 8 times faster than our PC process in 10 seconds?
  3. How much faster would a computer have to be than our PC to process a list of size 10 in a second?
15. An algorithm of with time complexity function T, where $T(n) = 2n \log{n}$, can process a 32 element list in 2 minutes and 40 seconds on our PC.
  1. How long would it take to process a 64 element list?
  2. If we ran the algorithm on a machine that was 4 times faster than our PC, how large of a list could we process in 16 seconds?
16. An algorithm with complexity function $T(n) = n^2$ processes a 100-element list in two minutes on our PC.
  1. How long does it take to process a 200-element list?
  2. How large of a list could a computer that is 2500 times faster than our PC process in a minute?
  3. How much faster would a computer have to be than our PC to process an element of size one billion in a second?
17. An algorithm with complexity function $T(n) = 2^n$ can process a 30-element list on our PC in 512 seconds.
  1. How many days would it take to process a 40-element list?
  2. How many years would it take to process a 50-element list?
  3. If we ran the algorithm on a machine that was one billion times faster than our PC, how large of a list could we process in one day? (Note 1 day = 86400 seconds)
  4. If we needed a computer that could process 80 elements in a week, how much faster than our original PC does this computer need to be? (1 week = 604800 seconds)
18. An algorithm with complexity function $T(n) = n^4$ can process a 16-element list on our PC in 256 seconds.
  1. How much time is needed to process a 32-element list?
  2. If we ran the algorithm on a machine that was 1024 times faster than our PC, how large of a list could we process in one day? (Note 1 day = 86400 seconds)
  3. If we needed a computer that could process 100 elements in a minute, how much faster than our original PC does this computer need to be?
19. Sometimes you will see the complexity function $\widetilde{O}$ — it is defined like this: $$ \widetilde{O}(f(n)) =_{def} \widetilde{O}(f(n)(\log{n})^k)$$ for some positive $k$. When an algorithm is known to have a complexity function in $\widetilde{O}(n^3)$, for example, some people will just say instead that it is in $\widetilde{O}(n^{3+\varepsilon})$ — where, of course, $\varepsilon$ is understood to be some arbitrarily small positive constant. Why is this okay?
20. One of the Freshmen tried to use the Master Theorem to solve $$ T(n) = \left\{ \begin{array}{ll} 1 & \mbox{if } n=1 \\ 2T(n-1) & \mbox{otherwise} \end{array} \right. $$
  Assuming you were kind and helpful, what would you tell this poor student? And, by the way, since kindness does not involve flat-out telling the student the answer, tell me, instead, how do you express $T$ in $\Theta$-notation?
21. Give the complexity function $T$ for the following code fragment, both as (a) a recurrence relation and (b) in closed form using Θ-notation.
```
public static long f(List a) {
    if (a.size() > 1) {
        f(a.subList(0, a.size()/2));
        f(a.subList(3*a.size()/8, 7*a.size()/8));
        f(a.subList(a.size()/4, 3*a.size()/4));
        f(a.subList(a.size()/8, 5*a.size()/8));
        f(a.subList(a.size()/2, a.size()));
        for (int i = 0; i < a.size(); i++) {
            for (int j = 0; j < i; j++) {
                System.out.print("*");
            }
        }
    }
}
```
22. Give the complexity function $T$ for the following code fragment, both as (a) a recurrence relation and (b) in closed form using Θ-notation.
```
public static long f(List a) {
    if (a.size() > 1) {
        f(a.subList(0, a.size()/3));
        f(a.subList(a.size()/3, 2*a.size()/3));
        f(a.subList(2*a.size()/3, a.size()));
        for (int i = 1; i <= a.size(); i *= 2)
            for (int j = 1; j <= i; j++)
                System.out.println("*");
            }
        }
    }
}
```
23. So you're reading this fancy paper on algorithms and you see a small snippet of code. It’s a recursive algorithm, with a small enough number of recursive calls that you can count them on one hand. The paper says that complexity of the algorithm is “obviously $\Theta(n^{2.32192809})$.”
  
  Explain the structure of the algorithm and how this “obvious” value was obtained.

Numeric Algorithms

Lehmann noticed that a number $p$ is prime if and only if for every $a$ less than $p$, $a^{(p-1)/2} = \pm 1\,(\mbox{mod}\:p)$ with at least one of the a's yielding -1 (In other words, they can't all yield 1). One of the Freshman wrote the following Java code to implement a probablistic Lehmann test, but there's a bug. What is the problem and how do you fix it?

public static boolean isProbablePrime(BigInteger n, int certainty) {
    boolean negativeOneFound = false;
    BigInteger negativeOne = BigInteger.ZERO.subtract(BigInteger.ONE);
    BigInteger half = n.subtract(BigInteger.ONE).divide(new BigInteger("2"));
    for (int i = 0; i < certainty; i++) {
        BigInteger a;
        do
            a = new BigInteger(n.bitCount(), random);
        while (!(BigInteger.ONE.compareTo(a) <= 0 && a.compareTo(n) < 0));
        BigInteger x = a.modPow(half, n);
        if (x.equals(negativeOne)) {
            negativeOneFound = true;
        } else if (x.equals(BigInteger.ONE)) {
        } else {
            return false;
        }
    }
    return negativeOneFound;
}

Cryptography
1. Generate the ciphertext for the message "RATSRULE" using the bifid algorithm with key "MICEAREEXTRAORDINARILYSTUPID". Lay out the key row by row, left to right within each row, as is the convention. Show the entire derivation.
2. Generate the ciphertext for the message "woohoo" using the bifid algorithm with key "THEQUICKBROWNFOX". Lay out the key row by row, left to right within each row, as is the convention. Show the entire derivation.
3. One of the seniors claims to be able to recover a DES-encrypted message with only 2⁵⁰ operations. If true, how big of an improvement is this over a brute-force attack? (You may answer in fractions or percentages.)
4. Write a Java, Python, or Julia function to generate three values $N$, $e$, and $d$, that can be used for an RSA key pair. Make $N$ a 512-bit number. For simplicity, you can let $e=3$. Write nice, short, elegant code.
5. Why, in practice, do people sign hashes of messages rather than whole messages?
String Algorithms
1. Give a Huffman Encoding for the string "THE CAT ATE THAT HAT". Hint: There are 6 T's, 3 H's, 2 E's, 4 spaces, 1 C, and 4 A's. That's 20 characters total.
Sorting
1. Consider the problem of sorting $n$ $k$-bit numbers.
  1. When, if ever, is Counting Sort feasible? Explain.
  2. Give the best and worst case time complexities of Radix Sort.
  3. Give the best and worst case time complexities of Quick Sort.
  Answers should use $\Theta$ notation, where both $n$ and $k$ are variables in the complexity functions.
2. Show the progress of (a) an insertion sort and (b) mergesort, applied to the array [45 21 3 99 14 17 88]. "Show the progress" means show the array after each pass.
3. Show the progress of (a) radix sort (base 10, LSD) and (b) selection sort, applied to the array [245 221 103 99 214 117 288].
4. Why is Quicksort usually faster than Mergesort when the data to be sorted is stored in an array?
5. Describe the best and worst case situations for Heapsort. That is, state which permutations of the input array result in the best and worst case running times for the algorithm.
6. Describe the best and worst case situations for Treesort.
7. Describe the best and worst case situations for Insertionsort. Why is its best case better than the best case for the other sorting algorithms you know? Why is its worst case worse than the worst case for the other algorithms?
8. Write a Python script to implement bogosort on a list.
Graphs and Graph Algorithms
1. For the following graph:
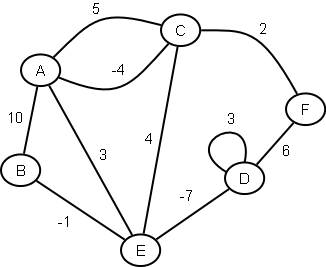
  1. How many blocks are there?
  2. Give a Depth First Traversal.
  3. Give a Breadth First Traversal.
  4. Give a Minimum Spanning Tree.
  5. Can Dijkstra's algorithm be used to find a shortest path from $F$ to $B$?
  6. Give the shortest path from $F$ to $B$.
  7. Is this graph simple? Why or why not?
  8. Which edges are bridges?
  9. Which nodes are articulation points?
  10. Is there a Hamilton cycle? If so, name one. If not, why not?
  11. Identify a trail (any trail).
  12. Is there an Euler tour? If so, name one. If not, why not?
  13. Give a smallest vertex cover.
  14. What is the degree of node $D$?
  15. How many isolated nodes are there?
  16. Is the graph complete?
  17. What is the chromatic number of this graph?
  18. What is the maximum flow of this graph?
2. Consider the undirected, weighted graph with vertices $\{A, B, C, D, E, F\}$ and edges $(A,B,5)$, $(B,D,6)$, $(B,C,1)$, $(A,C,3)$, $(F,E,2)$, $(D,E,2)$, $(E,C,8)$, $(A,E,1)$, and $(C,D,1)$.
  1. Draw the graph.
  2. Give a smallest vertex cover.
  3. Give a Minimum Spanning Tree.
  4. Use Dijkstra's algorithm to find a shortest path from $F$ to $B$.
  5. Which edges are bridges?
  6. Which nodes are articulation points?
  7. Is there a Hamilton cycle? If so, name one. If not, why not?
  8. Is there a Hamilton path? If so, name one. If not, why not?
  9. Is there an Euler path? If so, name one. If not, why not?
  10. What is the chromatic number of this graph?
  11. Solve the TSP for the graph obtained by removing node $F$.
3. Does the adjacency list representation of a graph have any advantages over other representations? If so, what are these advantages?
4. Does the following function really determine whether or not a given simple, undirected graph has cycles? (Recall that a cycle in a simple undirected graph is a simple circuit whose length is greater than or equal to 3.) I mean, every time I draw up a graph with as many or more edges than nodes I find cycles. Am I missing something, or have I really found an O(1) solution?
```
public static boolean hasCycles(Graph g) {
    return g.numberOfEdges() >= g.numberOfNodes();
}
```
  Why or why not?
5. Prove that a graph is 2-colorable if and only if it has no odd-length circuits (König's Theorem).
6. Use graph theory to prove that in any group of six people, there are either three people that all know each other or three mutual strangers. (Hint: talk about cliques and independent sets.)
7. The complement of a simple, undirected graph $G = (V,E)$ is the graph $G^C = (V,E')$ where $E' = \{(u,v)\:\mid\:(u,v) \notin E\}$. Less formally, $G^C$ contains exactly those edges that are not in $G$.
  1. Is it easier to compute the complement of a graph under an adjacency matrix or an adjacency list representation?
  2. Write a method of a SimpleUndirectedGraph class that returns its complement.
  3. What is the (time) complexity of your algorithm?
8. Show how to find, in polynomial time, the smallest independent set that is also a vertex cover.
9. How many edges are there in the complete graph $K_n$?
10. Traverse the following graph (a) breadth-first and (b) depth-first starting at node F:
  A — B — C — D — E — F — G — H — I — J
11. Note that, for a simple, undirected graph with $n$ nodes, the $n \times n$ adjacency matrix $M$ is space-inefficient.
  1. Exactly how many entries in the matrix $M$ are actually required to represent the graph?
  2. To save space we could store the significant entries of $M$ in a one-dimensional array $A$. We would then need a function $f$ such that $M(i,j) = A(f(i,j))$. Write the closed-form expression for $f$. (Assume that nodes are indexed from $1 ... n$.)
12. Is a Hamilton Path guaranteed to exist in a simple, undirected graph whenever the number of edges exceeds twice the number of nodes? Why or why not?
13. Prove that the sum of the degrees of the nodes in a simple, undirected graph is twice the number of edges in the graph.
14. Determining whether a simple, undirected graph is 3-colorable is NP-complete, but determining whether it is 2-colorable is in P. Give a $\Theta(e)$ algorithm for determining 2-colorability.
15. Write functions to compute the smallest dominating set and the maximum clique of a simple undirected graph.
16. What is the chromatic number of a full ternary tree of height $n$?
17. Prove that if a simple undirected graph $G$ is a tree then $G^C$ is either (1) connected or (2) consists of two blocks: one containing only one node and the other a clique of the remaining nodes.
18. Give the (time) complexity of Prim's algorithm for finding the minimum spanning tree of a graph, assuming that the priority queue is implemented as a heap.
Dynamic Programming
Search Algorithms
Randomized Algorithms
1. Is bozosort an example of a Las Vegas or Monte Carlo algorithm?
2. Is bogosort an example of a Las Vegas or Monte Carlo algorithm?
3. Why is it a good idea to randomize (scramble) an array before applying quicksort?
4. What does it mean for a random number generator to be cryptographically secure?
5. If you wanted to determine the probability that at least two people in a randomly selected group of thirty had the same birthday, you could run hundreds of trials and keep track of all the simulation results. Is this a Las Vegas or Monte Carlo algorithm?
Problem Reduction
1. Suppose you were given (1) an algorithm to compute the complement of a simple, undirected graph and (2) an algorithm to find the maximum clique in a simple, undirected graph. How could you then compute the smallest vertex cover?
2. Suppose I gave you an algorithm, to determine for some value $n$, whether or not a simple, undirected graph $G$ had a spanning tree in which no node had degree larger than $n$. Show how to use this algorithm to determine whether or not a graph has a Hamilton Path.
3. If you had an algorithm to solve the traveling salesperson problem you could use it to determine whether or not a graph had a Hamilton Circuit. How?
Complexity Classes and Approximation Algorithms
1. Explain informally but precisely why the problem "Does graph $G$ have a vertex cover of size less than or equal to $k$?" is in NP.
2. A problem that looks very much like the previous problem, namely "Does graph $G$ have a vertex cover of size greater than $k$?" is also in NP. In fact, its time complexity is $\Theta(1)$. Prove this. You can write a one-line function for your proof.
3. Give a polynomial time algorithm that returns “one of the smallest” vertex covers in a graph. It doesn't have to return the smallest vertex cover (it is not likely that you could do this in polynomial time anyway, why?) but its size should be close to minimal.
4. Give a function to find a "nearly maximal" independent set for a given simple undirected graph, using a greedy algorithm. Then give an example of a graph for which your algorithm gives a sub-optimal answer.
5. A logical formula is said to be satisfiable if and only if there exists some assignment of values to variables such that the formula evaluates to True. For example, the formula
```
(x1 or x3 or not x2) and (x2 or not x3)
```
  is satisfiable under the assignment x1 = True, x2 = False, x3 = False.
  1. Is this formula satisfiable?
```
(x1 or x3 or x5) and (x1 or not x2 or x4) and
  (not x3 or x4 or x5) and (x2 or not x3 or x5)
```
  2. Explain how you could determine if a graph were 3-colorable using a pre-existing algorithm for determining satisfiablility.
6. Is it easier or harder (from a computational point of view) to determine satisfiability or unsatisfiability?
7. It is thought that P ≠ NP because finding solutions seems to be a more difficult task than checking the validity of a candidate solution. Analyze the stable marriage problem to determine if it is ``easier'' (more efficient) to check that a given configuration is stable than to find a stable solution.
8. Consider the function C defined recursively as follows:
```
C(n, k) = 1, if k = 0 or k = n
        = C(n-1, k-1) + C(n-1,k) if 0 < k < n
        = undefined, otherwise
```
  It can be shown that C can also be defined non-recursively:
```
    C(n,k) = n! / (k!(n-k)!)
```
  Give the worst-case complexity of (a) the naïve recursive, (b) the non-recursive algorithms for computing C($n$, $k$).
9. Implement the function C above using dynamic programming.
10. Does the stable marriage problem always have a solution, provided the inputs (i.e. the preference lists) are legal? Give a proof or a counterexample.