Backtracking
About
Backtracking is an approach to solving constraint-satisfaction problems without trying all possibilities.
Constraint Satisfaction Examples
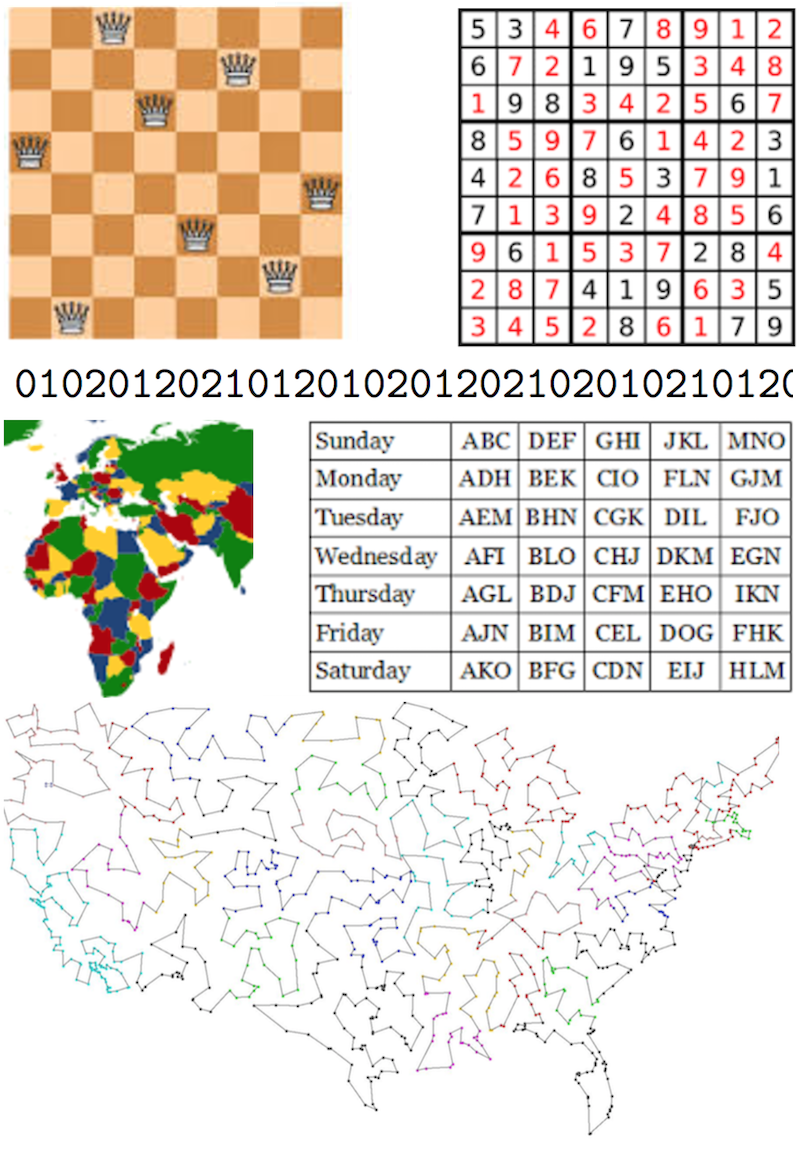
These problems are interesting because there are so many candidate solutions, the vast majority of which do not satisfy the given constraints. Can’t we just try them all, one-by-one, until one does? Not really, because:
- In the N-Queens Problem, there are ${n^2 \choose n}$ ways to place $n$ queens on an $n \times n$ board. For an $8 \times 8$ board there are 4,426,165,368 possible arrangements.
- For Sudoku, there are $9^n$ ways to fill the $n$ blank squares. Suppose we were given 20 cells filled in. There are 16,173,092,699,229,880,893,718,618,465,586,445,357,583,280,647,840,659,957,609 possible ways to fill in the remaining 61 cells.
- For the No Equal Adjacent Substrings Problem, there are $n^k$ possible strings. That’s a huge number. For a 100-character long string of trinary digits, we have 515,377,520,732,011,331,036,461,129,765,621,272,702,107,522,001 possibilities.
- When k-coloring maps of n regions, there are $k^n$ possible colorings. For example, there are 1,267,650,600,228,229,401,496,703,205,376 ways to color a 50-region map with 4 colors.
- There are $(15!)^7$ ways to arrange the walkers in a 7-day Kirkman Schoolgirls Problem. That is an 85-digit number.
- In the Traveling Salesperson Problem, there are $n!$ possible paths. 200! is a 375-digit number. 500! has 1,135 digits.
A brute-force algorithm tries all possibilities. Not going to happen.

Being Smart About the Solutions To Try
Think about how you would solve the no-equal-adjacent-substring problem.
Would you try to build up a solution, digit-by-digit? Click the STEP button to take a step at a time and see if it matches your intuition:
Visualize the problem as “filling in slots.” For each slot, try each value in turn. When a value doesn’t work in a slot, you’ve effectively eliminated zillions of candidates. When nothing works in a slot, you have to backtrack.
Let’s see more examples. For each example,
- Notice the formulation of the problem into slots and values.
- Watch carefully for the occurences of backtracking.
Eight-Queens
For each column (1..8), try to place a queen in each row (1..8) in turn, so that no two queens attack each other.
Map Coloring
For each country, try the colors red, green, orange, yellow in turn, so that no two adjacent countries have the same color.
No Equal Adjacent Substrings
For each slot 1..50, try the digits 0, 1, and 2 in order, such that no two adjacent substrings are equal.
Sudoku
For each non-fixed square, try each of the values 1..9 in turn. (Yes, there are better ways, but this will do for now.)
Maze Solving
At each square, try going up, then left, then right, then down. Whenever the new square has not been visited, move there. When you have to backtrack, mark the square as fully explored.
The Kirkman Problem
We’ll go over this one in class.
We Are Pruning Search Trees
If you had to systematically enumerate all possible candidate solutions to a “slots-and-values” problem, you might write them all out as paths in a tree. Each root-to-leaf-path is a candidate solution. Here are the candidates for the no-equal-substring problem, using the digits 0, 1, and 2, of length 4:
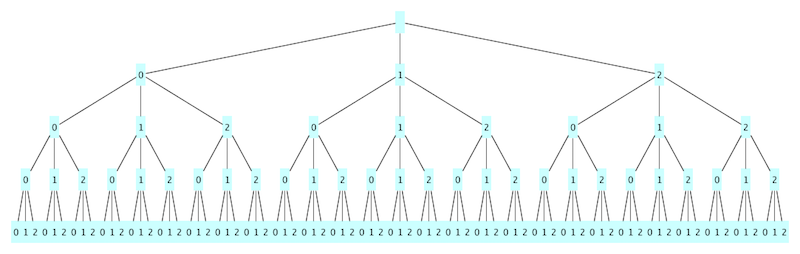
I only had room to show 4 levels (81 possible solutions, 121 nodes total); showing even 10 levels would require 59,049 leaf nodes (88,573 total nodes), and 50 levels would be, well, you get the idea.
To solve a constraint problem we search for a solution. A brute-force algorithm searchs the whole tree, but with backtracking, we get to throw away massive parts of the tree when we discover a partial solution cannot be extended to a complete solution. Notice:
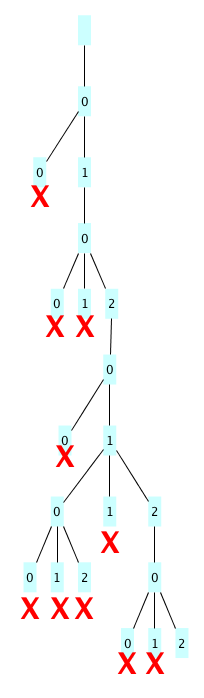
So after realizing the second value cannot be a zero, you can avoid considering (i.e., you prune) every possible string stating with 00. We built up a search tree with only 21 nodes, as opposed to 88,753.

A Generic Backtracking Solver
Each of the problems above are in the some sense the same problem. They all work by calling some initialization function, then for each possible slot, you try each possible value in turn, stopping when a solution is found, or backracking when we can’t fill the current slot. So we can write a backtracking engine that is parameterized by the type of slots, the values for each slot, and a function that determines whether the current partial solution is safe.
A Python Backtracking Engine
We just need a few lines for the Python engine:
def solve(values, safe_up_to, size):
"""Finds a solution to a backtracking problem.
values -- a sequence of values to try, in order. For a map coloring
problem, this may be a list of colors, such as ['red',
'green', 'yellow', 'purple']
safe_up_to -- a function with two arguments, solution and position, that
returns whether the values assigned to slots 0..pos in
the solution list, satisfy the problem constraints.
size -- the total number of “slots” you are trying to fill
Return the solution as a list of values.
"""
solution = [None] * size
def extend_solution(position):
for value in values:
solution[position] = value
if safe_up_to(solution, position):
if position >= size-1 or extend_solution(position+1):
return solution
return None
return extend_solution(0)
Here it is in action, solving the no-equal-adjancent substrings problem:
import backtracker
def no_adjacencies(string, up_to_index):
# See if the sequence filled from indices 0 to up_to_index, inclusive, is
# free of any adjancent substrings. We'll have to try all subsequences of
# length 1, 2, 3, up to half the length of the string. Return False as soon
# as we find an equal adjacent pair.
length = up_to_index+1
for j in range(1, length//2+1):
if (string[length-2*j:length-j] == string[length-j:length]):
return False
return True
print(''.join(str(v) for v in backtracker.solve(range(3), no_adjacencies, 50)))
$ python3 neas.py 01020120210120102012021020102101201020120210120102
And in the 8-Queens problem:
import backtracker
def no_conflicts(board, up_to_column):
# See if any queens in columns to the left of up_to_column interfere with
# the queen in up_to_column. Return False as soon as you find one that does.
for col in range(up_to_column):
if (board[col] == board[up_to_column] # same row
or board[col] == board[up_to_column] + up_to_column - col # diagonal
or board[col] == board[up_to_column] + col - up_to_column): # diagonal
return False
return True
print(backtracker.solve(range(8), no_conflicts, 8))
$ python3 queens.py [0, 4, 7, 5, 2, 6, 1, 3]
A Java Backtracking Engine
For kicks, let’s do the Java engine as a class designed for subclassing. Is this the best way? I really don’t know. Perhaps we should ask this on Codereview dot StackExchange dot com. (Seriously, why not?)
import java.util.Optional;
/**
* An engine for solving problems with the backtracking paradigm.
*
* <p>
* Solve a particular problem by subclassing this class, implementing the method
* that determines whether a partial solution is conflict-free so far.
*/
public abstract class BacktrackingSolver {
/**
* Subclass-specific method that returns whether or not the partial solution in
* slots 0..position-1 is okay so far.
*/
protected abstract boolean safeUpTo(int[] solution, int position);
/**
* Returns a solution to the problem, or throws a NoSuchElementException if
* there is no solution.
*/
public final int[] solve(int solutionLength) {
return extendSolution(new int[solutionLength], 0).get();
}
/**
* The fixed "engine" that is not overridden in subclasses.
*/
private Optional<int[]> extendSolution(int[] solution, int position) {
for (int value = 0; value < solution.length; value++) {
solution[position] = value;
if (safeUpTo(solution, position)) {
if (position >= solution.length - 1 || extendSolution(solution, position + 1).isPresent()) {
return Optional.of(solution);
}
}
}
return Optional.empty();
}
}
Here we use the engine to solve the queens problem:
import java.util.Arrays;
import java.util.NoSuchElementException;
/**
* A specialization of the BacktrackingSolver to find a solution to the
* N-queens problem. Includes a main method to print a solution to the
* problem where the board size is given as a command line argument.
*/
public class QueensSolver extends BacktrackingSolver {
/**
* Determines if the queen was safely placed in column index by seeing if
* its placement conflicts with any queen in columns 0..index-1.
*/
protected boolean safeUpTo(int[] solution, int index) {
int thisColumn = index;
int thisRow = solution[index];
for (int c = thisColumn-1; c >= 0; c--) {
if (solution[c] == thisRow ||
solution[c] == thisRow + thisColumn - c ||
solution[c] == thisRow + c - thisColumn) {
return false;
}
}
return true;
}
public static void main(String[] args) {
try {
int size = args.length < 1 ? 8 : Integer.parseInt(args[0]);
System.out.println(Arrays.toString(new QueensSolver().solve(size)));
} catch (NumberFormatException | NegativeArraySizeException e) {
System.err.println("Argument should be a nonnegative integer");
} catch (NoSuchElementException e) {
System.err.println("No solutions for this board size");
}
}
}
$ javac QueensSolver.java & java QueensSolver 8 [0, 4, 7, 5, 2, 6, 1, 3] $ javac QueensSolver.java & java QueensSolver 2 No solutions for this board size $ javac QueensSolver.java & java QueensSolver -5 Argument should be a nonnegative integer $ javac QueensSolver.java & java QueensSolver dog Argument should be a nonnegative integer $ javac QueensSolver.java & java QueensSolver 18 [0, 2, 4, 1, 7, 14, 11, 15, 12, 16, 5, 17, 6, 3, 10, 8, 13, 9]
Iterative Implementations
The solutions above used recursion to implement backtracking. This is great because if we ever have to backtrack, we return right in the middle of a for-loop so we know the next value to try. This is actually awesome.
Can we do things iteratively?
Well, yeah, but we have to some incrementing an decrementing manually, and some ugly loop controlling.

Here’s a crack at an iterative engine in Python:
def solve(highest_value, safe_up_to, num_slots):
"""Finds a solution to a backtracking problem.
highest_value -- the largest value to try. Values for the slots will be in
the range 0..highest_value, inclusive.
safe_up_to -- a function with two arguments, solution and position, that
returns whether the values assigned to slots 0..position
in the solution list, satisfy the problem constraints.
num_slots -- the total number of “slots” you are trying to fill
Return the solution as a list of values.
"""
solution = [None] * num_slots
def solve_from(position):
while True:
if safe_up_to(solution, position):
if position >= num_slots-1:
# We filled the last slot and everything is okay
return solution
position += 1
solution[position] = 0
else:
# Backtrack. We might have to undo several slots, so....
while (solution[position] == highest_value-1):
solution[position] = None
position -= 1
if position < 0:
break
solution[position] += 1
# We backtracked beyond the starting point, meaning we could not find
# a valid value for the first slot, so no solution
return None
# With the iterative solution, I think you have to begin by priming the
# solution list with the first value in the first slot.
solution[0] = 0
return solve_from(0)
Estimating the Size of the Backtracking Tree
See the section entitled Knuth’s Method of this paper.
Branch and Bound
Sometimes it’s not good enough to find just one solution. Sometimes you have to find the best solution. We will look at two examples.
Coin Changing
Let’s try to find the minimum number of coins to make change from 8 cents, given that our coin denominations are 5 cents, 4 cents, and 1 cent: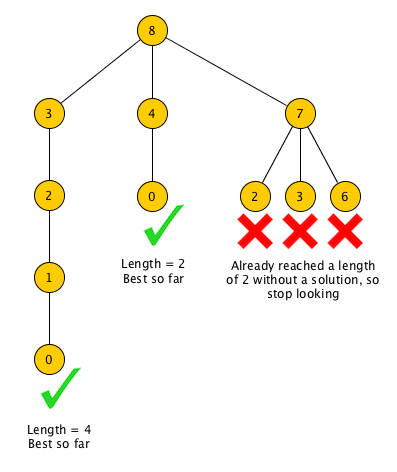
We used a branch and bound approach. We started with 8 cents at the root. We branched by trying a new coin. We bounded our search whenever we found that there was no reason to keep going down our current path, since we had already reached (or passed) the best result we found so far.
The optimal solution to a branch-and-bound problem isn’t known until you have expanded the whole search tree, but the hope is that you’ve done a great job ordering your branches so you’ll bound like crazy.
But what if your constraints and your inputs are such that you don’t get to bound much, and your asymptotic complexity is exponential, and your input size is massive? You can still branch and bound, but you know what? Maybe just run the algorithm for long enough and just take the best so far.
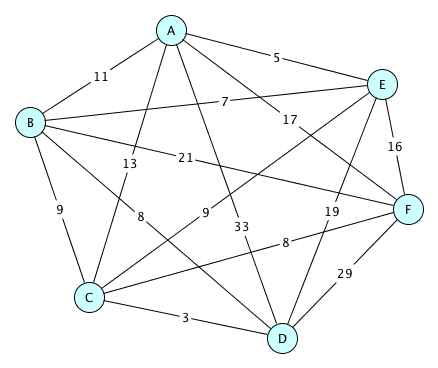
Traveling Salesperson
Here’s one for you to try on your own.
What’s Next?
Brute-force search and backtracking (perhaps with branch and bound) are generally where we start learning about search. But the fun stuff is yet to come. You’ll learn about heuristics, randomization, and performing parallel searches with multiple agents. There is hill climbing and simulated annealing. And some of these problems can be solved with dynamic programming. There are entire programming languages built around constraint solving. And there are tons of subfields of mathematical optimization.
This stuff is huge in artificial intelligence and machine learning.
But please don’t forget to think outside the algorithms box.
