Computability Theory
History
David Hilbert was good at formal logic. He wondered about many things.
He challenged mathematicians of his day with many problems.
Thinking there might be a way to algorithmically determine the truth or falsity of any statement in an axiomatic system, he posed the Entscheidungsproblem.
Philip Wadler tells the story:
Computation has limits. Mathematicians and programmers will never go out of business. Computer Science will always be an interesting field. We can dig deeper into this field of computation, and in particular, study what it means to be computable.
Models of Computation
We learned form Wadler that all three of these:
- Church’s λ-calculus
- Gödel’s μ-recursive functions
- Turing’s Turing Machines
were equivalent. It turns out that a bunch of other efforts to formalize computation were also equivalent:
- Chomsky’s Phrase-Structure Grammars
- String Rewriting Systems (also known as Semi-Thue Systems)
- Post’s Post Production Systems
- All sorts of crazy extensions to Turing Machines (except magic oracles)
Because all of these formalisms are equivalent, and no one has found something better (other than magic oracles), most folks hypothesize that we really have formally captured our intuitive notion of computability with these things. The Church-Turing Thesis states that what we intuitively understand by “computation” is captured by the Turing Machine.
Limits of Computation
In retrospect, one wonders why Hilbert suspected that every mathematical statement (i.e., a statement of a “formal axiomatic systems capable of representing arithmetic and beyond”) was decidable! And thus, whether all true statements had proofs, or why there should exist a finite algorithm that could compute all functions in $\mathbb{N} \rightarrow \mathbb{N}$ (or even in $\mathbb{N} \rightarrow \mathbb{B}$).
For example, a simple diagonalization proof tells you there are non-computable functions in $\mathbb{N} \rightarrow \mathbb{N}$:
Proof: Programs are finite strings of symbols so there are a countably infinite number of them. If all functions were computable, then there would need to be a program for each one, so there would need to be a countably infinite (enumerable) number of functions. If we could enumerate every function from $\mathbb{N} \rightarrow \mathbb{N}$ as $f_0, f_1, f_2, \ldots$, then the function $f$ such that $f(n) = f_n(n)+1$. would not be on the list. So the list is incomplete.
We’re going to write out this diagonalization on the board.
Okay nice, so there are more functions than programs. But are there any realistic functions we can specify that we cannot decide?
A Simple Non-Decidable Problem
Do there exist problems for which all instances have a YES-NO answer but no computer, no matter how powerful, nor any algorithm, in any formalism whatsoever, can compute the answer?
Of course, as we’ve shown above, a simple counting algorithm tells us that yes, they must exist! But are there any that we can describe and actually understand? Yes, and here’s the classic first example. It is known as The Halting Problem:
Write a function called halts, which accepts a function f and an input x, and returns True if f(x) halts, and False if f(x) enters an infinite loop when run.
Sounds simple enough. Let’s assume we can write it:
def halts(f, x): # TODO: code to decide the issue and return True or False
But here’s the problem. Let’s consider this, perfectly normal function:
def fox(f): if halts(f, f): while True: pass
The expression fox(fox) leads to an inconsistency: Running fox(fox) does this: "if halts(fox, fox) then go into an infinite loop, otherwise halt.” Ugh. Wait. OMG. This cannot be. So our assumption that halts could be written must be incorrect. We cannot write halts in any programming language. The halting problem is undecidable.
Python?
It’s way more fun to use Python in these proofs, but when we do, keep in mind these are isomorphic to language decision problems. In the Halting Problem case, we can re-cast this whole “problem” into one of deciding a particular language, namely: $$\mathcal{H} = \{ \langle M \rangle w \mid M \textrm{ halts on } w \}$$ where $\langle M \rangle$ is the string encoding of machine $M$.
Remember: Recognizable vs. DecidableRecall that a language is recognizable if there is a Turing Machine accepts (answers YES) for all and only those strings in the language. A language is decidable if there is a Turing Machine that accepts (answers YES) for all strings in the language and rejects (answers NO) for all strings not in the language. A recognizer may either, for strings not in the language, loop or answer NO. A decider must always halt with a YES or NO answer. All deciders are recognizers but not vice-versa.
Recognizability
One of the more interesting things to come out of computability theory is that there are some languages that Turing Machines can recognize, but not decide. The language of all machine+input pairs that halt is one such language.
But guess what: Even though you can’t decide whether a program will halt, you can recognize whether a program will halt:
def halts(f, x): f(x) return True
So the language of halting programs is recognizable but not decidable.
The formal (mathematical) argument goes like this: If you can recognize a language, you can enumerate all its utterances. For concreteness, let’s see how this is done with the Halting Problem. Since all programs are strings we can enumerate a list of all programs $p_0, p_1, p_2, p_3, \ldots$. We can do this:
- At time $t_1$, run one step of $p_0$
- At time $t_2$, run two steps of $p_0$ and one step of $p_1$
- At time $t_3$, run three steps of $p_0$, two steps of $p_1$, and one step of $p_2$
- ...
...and so on. Whenever a $p_i$ halts, add it to your “output list” of halting programs.
This process enumerates all and only the halting programs.
We have the following fact:
The set of all languages that are Turing-Recognizable is known as RE, namely, the set of Recursively Enumerable Languages.
and also:
The set of all languages that are Turing-Decidable is known as R, namely, the set of Recursive Languages.
The fact that $R$ is a proper subset of $RE$ surprised some people. It is saying that languages—and therefore some decision problems— for which we can definitely compute a YES answer...but when the answer is NO we might...never...know.
🤯
Beyond Recognizable
Now what about the language of all strings that encode Turing Machines that never halt (sometimes called $\bar{H}$)? That language isn’t even recognizable. This will need a proof, but we’ll get there soon.
So, how do we know a language isn’t recognizable?
We can find a first non-recognizable language using diagonalization. The language is called $\mathcal{X}$ and is defined by:
$$ \mathcal{X} = \{ \langle M \rangle \mid M \textrm{ does not recognize } \langle M \rangle \} $$(Informally, it is the set of all machines that don’t recognize themselves.) To show this language is not recognizable by any Turing Machine let’s make a list of all the Turing Machines there can possibly exist. There are a countably infinite number of these. We will call them $M_0, M_1, M_2, \ldots$. For each machine we will write out whether it recognizes the encodings of all of the machines:
| $\langle M_0 \rangle$ | $\langle M_1 \rangle$ | $\langle M_2 \rangle$ | $\langle M_3 \rangle$ | ... | |
|---|---|---|---|---|---|
| $M_0$ | T | F | F | T | ... |
| $M_1$ | T | T | T | T | ... |
| $M_2$ | F | F | F | T | ... |
| $M_3$ | T | T | F | T | ... |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
The T’s in each row comprise the language recognized by $M_i$. The language $\mathcal{X}$ is the flipped diagonal of this table, which cannot appear in this table. No matter how we try to enumerate all the Turing Machines, there will never, EVER, be a row which makes $\mathcal{X}$. So $\mathcal{X}$ cannot be recognized by a Turing Machine.
Reductions
So the Halting Problem is undecidable. But how do we prove other problems undecidable? One way is to prove: “If problem $P$ were decidable, then the Halting Problem would also be decidable.”
This is done by reducing the Halting Problem to problem $P$.
In general, a reduction of problem $A$ to problem $B$ means we use an algorithm for $B$ to solve $A$. You’ve probably done that a lot in the past, right? You've written “utility functions” and then called them to do a larger task.
Let’s to this for the problem of determining whether $L(M) = \varnothing$. In formal notation, we want to know if we can decide:
$$\mathcal{E} = \{ \langle M \rangle \mid L(M) = \varnothing \}$$This is the empty language problem. We can reduce the halting problem to it. Let’s do it. Suppose $\mathcal{E}$ were decidable. This would mean we would have a machine $E$ that when given the description of a machine $M$ as input, would always halt with YES when $L(M) = \varnothing$ and halt with NO otherwise.
So let’s make a machine called $H$ that (1) takes two inputs, $\langle M\rangle$, the description of a Turing Machine, and $w$ a string, and produces the description of a machine that erases its input, writes $w$ on it, and simulates $M$, then (2) passes that new machine to $E$, then (3) swaps the outputs of $E$. Machine $H$ decides the halting problem. But this cannot be. The only place we could have gone wrong was our assumption that a decider for $E$ exists. So $\mathcal{E}$ is undecidable.
A diagram might help:
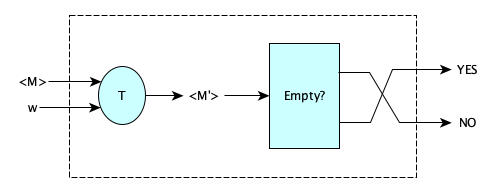
Here $L(M') = \varnothing$ iff $M$ does not halt on $w$, so the dashed box is a halting problem decider, which should not exist. So the Empty? machine cannot be a decider.
See Wikipedia’s article on reducing problems and Wikipedia’s list of undecidable problems.
Rice’s Theorem
Here is something amazing.
Let’s say you were given a general YES-NO problem about the run-time behavior of programs (e.g. does the program halt? or does this program ever output more than three symbols?). Rice’s Theorem says that the problem is undecidable unless the property holds for all programs or holds for none.
More technically: All nontrivial semantic properties of programs are undecidable.
Here semantic means run-time and trivial means holds for all or holds for none.
More at Wikipedia.
The Chomsky Hierarchy
The “limits” of computing models can define families of languages. For example:
| The languages that can be recognized by | are the ___ languages | which Chomsky called |
|---|---|---|
| Turing Machines | Recognizable, a.k.a. Recursively Enumerable (RE) | Type 0 |
| Turing Machines that always halt | Decidable, a.k.a. Recursive (R) | |
| LBA | Type-1 (CS) | Type 1 |
| NPDA | Context-Free (CF) | Type 2 |
| DPDA | Deterministic Context-Free (LR) | |
| FA | Regular (REG) | Type 3 |
| FA with no cycles | Finite (FIN) |
ALL OF THESE LANGUAGE FAMILIES ARE PROPER SUBSETS OF THE FAMILY IN THE ROW ABOVE IT.
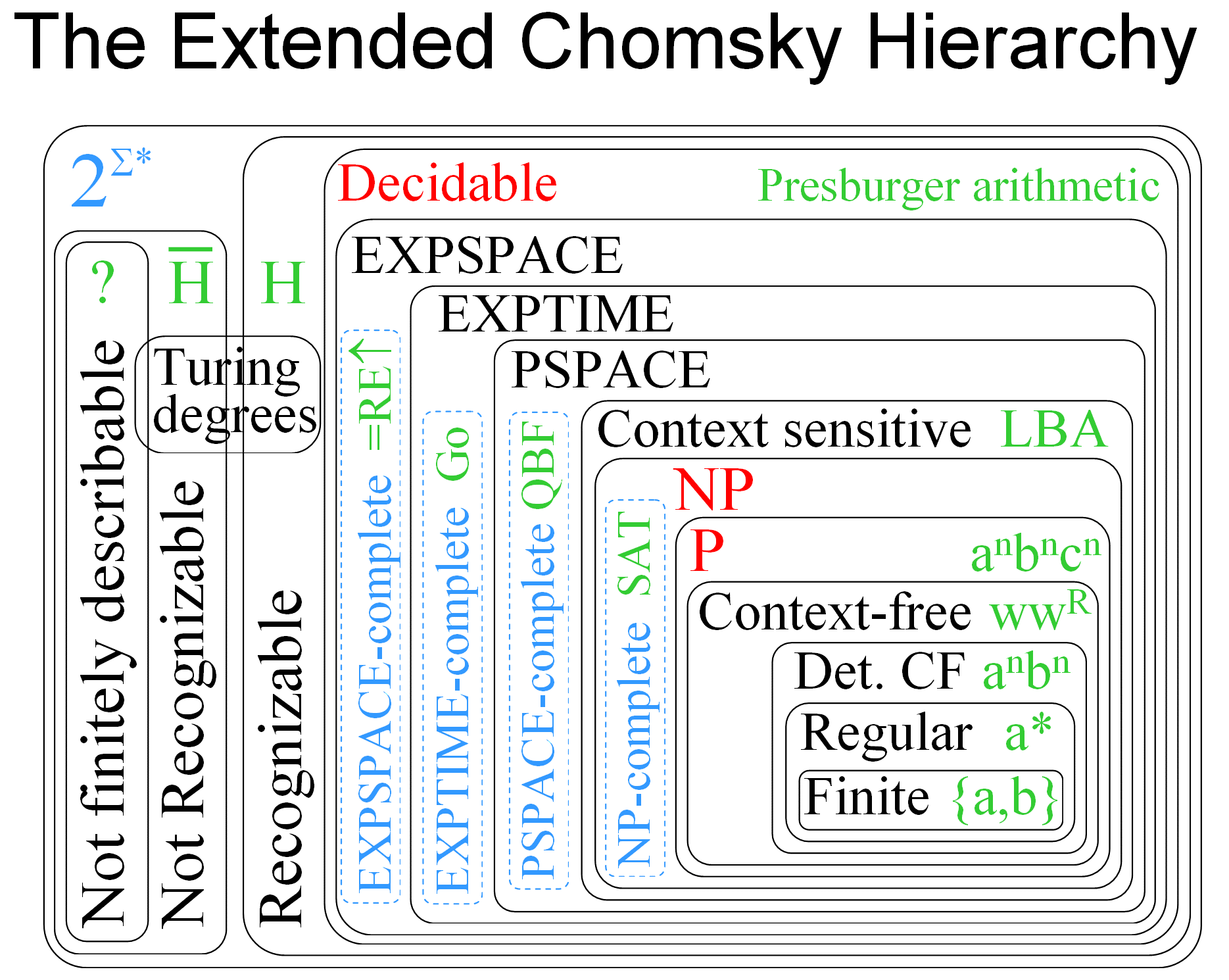
Gabe Robins has a beautiful visualization (which mixes in a few classes from complexity theory):
Oracles
Loosely speaking, an oracle is something you can add to a machine, that, at any time during a computation, you can simple “ask the oracle” a question whose answer might not even be computable. It just magically answers the question and you go about your business.
Read about oracles at Wikipedia.
Connections to Complexity Theory
Computability Theory deals with what can and cannot be computed on a particular computing model. It does not make any claims on the number of steps required, or the amount of space required, to do the computation. That is what complexity theory is for.
But you know, maybe we shouldn’t try to separate computability from complexity. These are convenient labels, but they are very inter-related. In fact, Robins’s diagram intentionally places complexity classes in with the standard computability classes. Many schools offer a course called Computability and Complexity. Erik Demaine at MIT gives a brief overview of the limits of computation within his complexity theory lecture in his 6.006 class:
Busy Beavers
An $n$-state busy beaver is a deterministic $n$-state halting Turing Machine with $\Sigma = \{ 1 \}$ and $\Gamma = \{b, 1\}$ that ... okay, well there are different kinds of busy beavers ... that, either:
- writes the largest number of 1s
- takes the largest number of steps
- visits the most number of squares
on an initially blank tape over the set of all such deterministic $n$-state halting Turing Machines.
Why on Earth would be care about such things?
They tell us something about the nature of computation. Seriously, these things are out of pocket.
Let’s get precise. First, let’s see what we are up against. Previously we saw that the number of deterministic $n$-state Turing Machines is either $(4n+1)^{2n}$ (for the halt-as-action variety) or $(4(n+1))^{2n}$ (for the halt-state variety). Hey, either way, that’s a lot of Turing Machines! For fun, here are the first few values:
| $n$ | $(4n+1)^{2n}$ | $(4(n+1))^{2n}$ |
|---|
So to find $BB(n)$ for a given $n$, we first note that some of these machines will halt, and some will not. Now we can go through all the halting ones (hahahahaha, oh my) and count the number of 1s they print, or the number of steps they take. The maximum number of printed 1s we find is $\Sigma(n)$, and the maximum number of steps taken is $S(n)$. (Today, most people care mostly about $S$, which they now call $BB$, so $S(n) = BB(n)$.) Let’s see what these values are:
| $n$ | $\Sigma(n)$ | $BB(n)$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 6 |
| 3 | 6 | 21 |
| 4 | 13 | 107 |
| 5 | 4098 | 47176870 |
| 6 | $> 10 \uparrow \uparrow 15$ | $> 10 \uparrow \uparrow 15$ |
Woah.
It seems amazing that we actually know what $BB(5)$ even is! Knowing this means that for each of the tens of trillions of possible 5-state, 2-symbol Turing Machines, someone figured out whether it halts or not, and if it halts, how many steps it took, and what it outputs.
That’s a lot of machines to go through. And it’s not easy to figure out whether a long-running machine will eventually halt or not. Such a machine might take years or centuries to finish, so we can’t just run it and see. In fact, there is no way to compute, in general, whether an aribtrary machine will even halt. We have to painstakingly analyze each machine, and we have to sometimes be really clever. And even if we know a long running machine will halt, we need a clever way to figure out its step count (or printed-1s count), because this number might be too big to actually store. At some point the numbers far exceed our human ability to currently even describe. A lot of ingenuity is required. People that try to find these values are called Busy Beaver Hunters.
Champions
Here are some busy beavers (from Pascal Michel). The notation below comes from bbchallenge, the Busy Beaver Challenge site. Here 0=blank.
BB(1) = 1
BB(2) = 6
BB(3) = 21
BB(4) = 107
BB(5) = 47,176,870
Learn More!
There are thousands of great resources to study. Here is a small sampling. Note that some of these exclusively use the halt-state variety and some exclusively use the halt-action variety and some mix them all up. Try not to get too lost!
- Wikipedia’s article
- The Busy Beaver Challenge Home Page
- Busy Beaver numbers at the OIS
- This video was made before the five-state Busy Beaver was known for sure:
- And here’s Jade with a video explaining the success in finding the five-state champion:
- A very nice short paper with formal proofs that $\Sigma$ and $S$ are uncomputable.
- Scott Aaronson’s BB Frontier paper from 2020
- Scott Aaronson’s article on the proof of BB(5)
- A great list of Busy Beaver known and current champions
- A little paper by Esther Fu and Sarah Pan
Busy Beaver Functions are not ComputableIt turns out that $\Sigma$ and $BB$ are not a computable functions. Although they are well-defined finite description, no computing device can compute them. Here's something really cool: They grow faster than any computable function.
Imagine that.
More Resources
Computability Theory is a fascinating subject.
You might also like:
- Gabe Robins’s Theory Course Notes from University of Virginia
- Some nice notes from a Columbia course
When studying Robins’s notes, focus on the set entitled “Formal languages, automata models, grammars, decidability, and Rice's theorem” (PDF here). There are several examples of problem reductions and of applications of Rice’s Theorem.
Summary
We’ve covered:
- A history of computability theory
- Models of computation
- Limits of computation
- The halting problem
- The difference between recognizability and decidability
- The idea of problem reduction
- Rice’s Theorem
- The Chomsky Hierarchy
- Oracles
- Connection to Complexity Theory
