Digital Logic

Gates
Most of mathematics (especially Axiomatic Set Theory and Number Theory) uses a bivalent logic, in which statements are either true or false. Electronic computers employ logic gates for the most primitive computations, taking 0 as false and 1 as true. An infinite number of gates are possible; here are six of the most common:
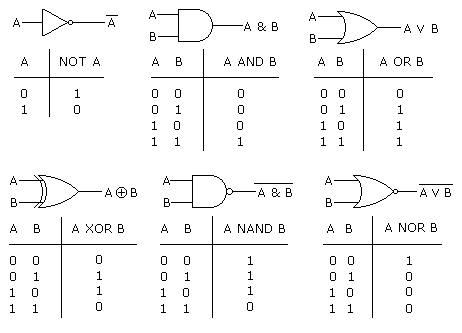
Why these names? Think of 0 as false and 1 as true. Then:
- “not A” has the opposite truth value of A
- “A and B” is true if and only if A is true and B is true
- “A or B” is true if and only if either A is true or B is true or both
- “A xor B” is true if and only if either A is true or B is true but not or both
- “A nand B” (“not and”) is the opposite of “A and B”
- “A nor B” (“not or”) is the opposite of “A or B”
Gates can be built out of pasta, rubberbands, or anything you like. Generally they are built from transistors. Here are how CMOS transistors can be used to build NOT, NAND, and NOR gates (the line at the top is 1; the line at the bottom is 0):
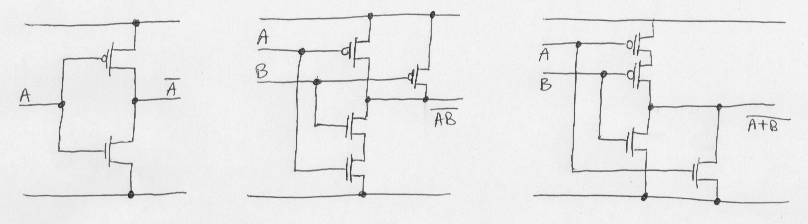
When studying computer systems organization, we generally take the gates as given, and leave it to the electrical engineers and computer engineers to worry about transistors and provide us with reliable gates.
Logic Computations
Operations can be extended to bit strings. Examples:
10110 01101 01101 01101
NOT AND 10100 OR 10100 XOR 10100
----- --------- -------- ---------
01001 00100 11101 11001
Bit Manipulations
Note the following useful formulas (just three among many)...
x AND 0 = 0 x OR 0 = x x XOR 0 = x x AND 1 = x x OR 1 = 1 x XOR 1 = ~x x AND x = x x OR x = x x XOR x = 0
...from which you can discover such tricks as:
- To set bits 2, 3 and 7 in an 8-bit word, OR with 8C
- To clear bit 6 in a 16-bit word, AND with FFBF
- To complement bits 2 and 3 in an 8-bit word, XOR with 0C
- To clear an entire word, XOR with itself
- To compute R mod 8, AND with 7
Binary Logic Functions
There are 16 possible two-input gates that can be created:
| A=0 B=0 | A=0 B=1 | A=1 B=0 | A=1 B=1 | Operation |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | $0$ |
| 0 | 0 | 0 | 1 | $A$ and $B$ $A \wedge B$ $AB$ |
| 0 | 0 | 1 | 0 | $A$ andnot $B$ $A \wedge \neg B$ $A\overline{B}$ |
| 0 | 0 | 1 | 1 | $A$ |
| 0 | 1 | 0 | 0 | $\neg{A} \wedge B$ $\overline{A}B$ |
| 0 | 1 | 0 | 1 | $B$ |
| 0 | 1 | 1 | 0 | $A$ xor $B$ $A \oplus B$ $A \neq B$ |
| 0 | 1 | 1 | 1 | $A$ or $B$ $A \vee B$ $A + B$ |
| 1 | 0 | 0 | 0 | $A$ nor $B$ $\neg(A \vee B)$ $\overline{A+B}$ $A \downarrow B$ |
| 1 | 0 | 0 | 1 | $A$ xnor $B$ $\neg(A \oplus B)$ $\overline{A \oplus B}$ $A = B$ |
| 1 | 0 | 1 | 0 | not $B$ $\neg{B}$ $\overline{B}$ |
| 1 | 0 | 1 | 1 | $A$ ornot $B$ $A \vee \neg{B}$ $A + \overline{B}$ $B \supset A$ |
| 1 | 1 | 0 | 0 | not $A$ $\neg{A}$ $\overline{A}$ |
| 1 | 1 | 0 | 1 | $\neg{A} \vee B$ $\overline{A}+B$ $A \supset B$ |
| 1 | 1 | 1 | 0 | $A$ nand $B$ $\neg(A \wedge B)$ $\overline{AB}$ $A \uparrow B$ |
| 1 | 1 | 1 | 1 | $1$ |
Wikipedia has long articles on most if not all of these. Don’t miss the ones on AND, OR, XOR, NAND, and NOR.
Equivalences
These are so important. Study them. Know why, exactly, they hold. Know their deep meanings. $$\begin{eqnarray} AA & = & A \\ A+A & = & A \\ A\overline{A} & = & 0 & \tiny \textrm{A can't be both true and false}\\ A + \overline{A} & = & 1 & \tiny \textrm{A is either true or false}\\ AB & = & \overline{\overline{A} + \overline{B}} & \tiny \textrm{both true iff not the case that either is false}\\ A + B & = & \overline{\overline{A} \: \overline{B}} & \tiny \textrm{either true iff not the case that both are false}\\ \overline{AB} & = & \overline{A} + \overline{B} & \tiny \textrm{not both true iff either is false}\\ \overline{A + B} & = & \overline{A} \: \overline{B} & \tiny \textrm{not the case that neither is true if both are false}\\ \end{eqnarray} $$
Complete Sets of Operators
An interesting intellectual exercise is to come up with what are known as complete sets of operations. A complete set is a set of operations from which all sixteen operations can be derived. For example {NOT, AND, OR} is complete, so is {NAND}. But {OR} is not complete.
Let’s prove {NOT, AND, OR} complete. To do so, we show how each of the sixteen operators can be defined using only NOT, AND, and OR. Here goes:
- $0 = A\overline{A}$
- $AB$ already uses only the desired operators
- $A\overline{B}$ already uses only the desired operators
- $A = AA$
- $\overline{A}B$ already uses only the desired operators
- $B = BB$
- $A \oplus B = A\overline{B} + \overline{A}B$
- $A + B$ already uses only the desired operators
- $\overline{A + B}$ already uses only the desired operators
- $\overline{A \oplus B} = AB + \overline{A}\,\overline{B}$
- $\overline{B}$ already uses only the desired operators
- $A + \overline{B}$ already uses only the desired operators
- $\overline{A}$ already uses only the desired operators
- $\overline{A} + B$ already uses only the desired operators
- $\overline{AB}$ already uses only the desired operators
- $1 = A + \overline{A}$
Now to prove {NAND} alone is complete, we just have to show how to define NOT, AND, and OR, in terms of NAND (then we can use the NAND-only versions of these three to make the rest, as we saw above):
- $\overline{A} = \overline{AA}$
- $AB = \overline{\overline{AB}} = \overline{(\overline{AB})\:(\overline{AB})}$
- $A + B = \overline{\overline{A} \: \overline{B}}$
Disgusting, ugly, and overcomplicated, yes, knowing that such things can be done has benefits.
- $A+\overline{BC}$
- $A\oplus{\overline{C}}$
- $AB\overline{C} + AC + D$
- $1$
Logic Circuits
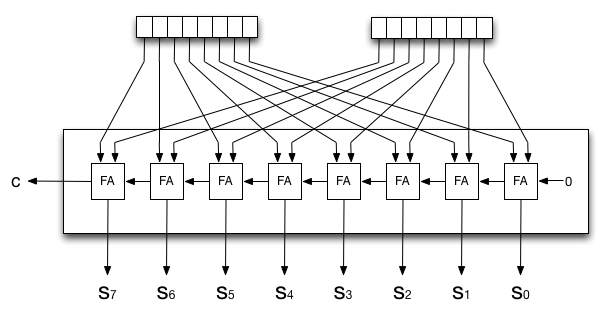
Logic designers create circuits to do things that they want. They basically want to implement functions that take certain inputs into certain outputs. For example, here is a logic circuit that adds two four-bit integers:
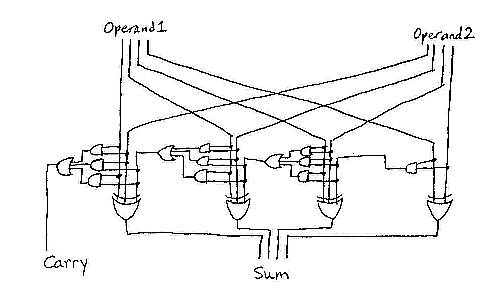
How did anyone figure this out? First let’s try the case where we only want to add two one bit numbers. Call the inputs x and y, and the outputs will be s (for sum) and c (for carry). Write down the behavior for all possible combinations of inputs:
x y | s c ------+------ 0 0 | 0 0 0 1 | 1 0 1 0 | 1 0 1 1 | 0 1
Cool, so we see that s = x XOR y, and c = x AND y. So here is our half-adder:
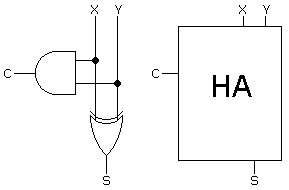
Now to add multi-bit numbers, we have add the carries into the inputs as we move from right to left, like you learned in elementary school. Thus the full-adder has three inputs, x and y and the carry in. Let’s make the table and see what we should do:
x y cin | s cout ---------+--------- 0 0 0 | 0 0 0 0 1 | 1 0 0 1 0 | 1 0 0 1 1 | 0 1 1 0 0 | 1 0 1 0 1 | 0 1 1 1 0 | 0 1 1 1 1 | 1 1
So s = x XOR y XOR cin and cout = (y AND cin) OR (x AND cin) OR (x AND y).
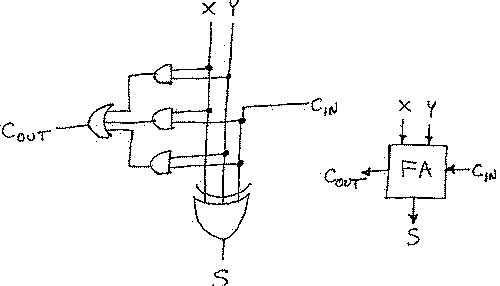
You can build a multibit adder by putting a half adder on the right and a sequence of full adders to its left, or just use full adders and force a zero into the rightmost carry in.
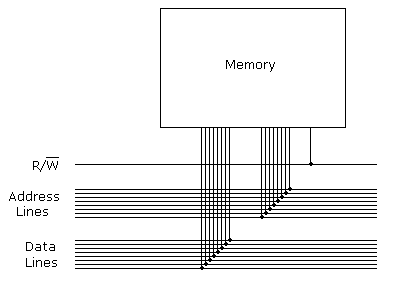
Memory Circuits
A read-only memory (ROM) is just a logic circuit whose input is an address and whose output is the data at that address! Make one by deciding what values go at what address and build the circuit however you need to.
What about a read-write memory? To read from memory, put the address you want to read from on the address lines, and set the read/write line to read. The value at that address will then appear on the data lines. To write, put the desired address on the address and the data to write on the data lines and set the read/write line to write.
But how do you store data? You probably use latches or something similar. A latch can store one bit. This is a latch:
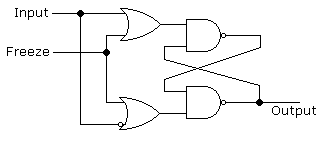
The idea is when you set Freeze to 0, the input value goes into
the latch. Then you set Freeze to 1. After that no matter what
the input does, the output is always what got copied in, so
we’ve “stored” a bit. Until you unfreeze it.