Expression Evaluation

Expressions

At a fundamental level, programming can be viewed as nothing more than applying functions to arguments. The fact that the Lambda Calculus exists and is shown to be Turing complete means this is true. But we don’t want to program directly in the Lambda Calculus. We like languages with nice-looking, readable syntax. Let’s visit a few examples:

F                        -- no parens for zero-operand operators
F (X, Y, Z)              -- three operands for operator F
"+" (X, Y)               -- abbreviated X + Y
">" (X, Y)               -- abbreviated X > Y

f()                      // parens required for zero-operand calls
f(x, y, z)
operator+(x, y)          // abbreviated x + y
operator>(x, y)          // abbreviated x > y

(f)
(f x y z)
(+ x y)
(+ a b c d e)            ; Not just binary
(+ x (* y z))

&f
f x, y, z                # Hmm, what does this mean?
f(x), y, z               # Not a call! Just a list of three things
f(x, y, z)               # Three-operand invocation
print 1, 3, sort 4, 2    # Gaaack

f ()                     (* ALL ops MUST have one operand, so () is a value! *)
f x y z                  (* same as ((f x) y) z *)
f (x, y, z)              (* uncurried *)
op+ (x, y)               (* abbreviated x + y *)

f                        // No parens is okay
f(x, y, z)               // Typical
x.+(y)                   // abbreviated x + y
df.format(date)          // abbreviated df format date

Operators

An operator is basically just a function. But usually, it means a function that has a special status in the language. It is usually but not necessarily named with non-letter (“symbolic”) characters, like “+” or “<” or “=>”. Common alphanumeric operator names are new, delete, and typeof.

Operators have:

• Precedence, which determines the order in which different operators are applied in an expression (higher precedence operators are applied first)
• Associativity, which determines how operators of the same precedence are grouped in an expression (left, right, or no-grouping-allowed)
• Arity, which is the number of operands an operator takes
• Fixity, which is the position of the operator relative to its operands (before, after, between, around, over, under, etc.)

Precedence

Does a•b¶c mean ((a•b)¶c) or does it mean (a•(b¶c))?

Higher precedence operators are applied before lower precedence ones.

Believe it or not, there are so many variations on this simple idea:

• Some languages have only one precedence level (e.g. APL, Smalltalk).
• Some languages have too many levels to memorize (e.g. C++, Perl).
• Some languages have very nonintuitive precedence definitions (e.g. Pascal).
• Perl’s distinction between named unary operators and other functions makes precedence impossible to distinguish by syntax alone.
• Standard ML allows the programmer to change precedence at run time.
• In languages where you can define your own symbolic operators, precedence can be defined by the programmer..

I wasn’t kidding about Standard ML. Check this out. When you start things up, Multiplication has precedence level 7 and addition has precedence level 6. We can change them:

5 * 3 + 2;
17
infix 7 +;

infix 6 *;

5 * 3 + 2;
25

Associativity

Does a•b•c mean ((a•b)•c) or does it mean (a•(b•c)) or are we not even allowed to write such a thing?

We speak of left associativity, right associativity, and nonassociativity. It is possible, but probably undesirable, for associativity to be unspecified in a language definition 😬.

Variations:

• In Smalltalk, every operator is left-associative (and has equal precedence).
• In APL, every operator is right-associative (and has equal precedence).
• In many languages, arithmetic is usually left-associative, except for exponentiation.
• There are good reasons for relational operators to be nonassociative, but most languages don’t do this very nice thing. If you design your own language, consider doing this.

Arity

The arity of an operator is the allowed number of operands. It can be fixed or variable. A variable arity operator is said to be variadic.

Fixity

There are a bunch of these: prefix, infix, postfix, overfix, underfix, outfix, and more. Examples in class.

Putting it all together

Many language definitions will feature operator tables such as the following:

The content of these tables vary surprisingly among different languages. It’s nice to have such tables so you can see at a glance how the language arranges its operators.

Some languages take pride in having a very small number of precedence levels. Here is the one for Standard ML. It does not mention unary operators because they are just regular functions. And all ”unary” functions bind tighter than (have higher precedence than) binary operators.

	Precedence	Associativity	Arity	Fixity
* / div mod	7	L	2	Infix
+ - ^	6	L	2	Infix
@ ::	5	R	2	Infix
< <= = <> >= >	4	L	2	Infix
:= o	3	L	2	Infix
before	0	L	2	Infix

And for Go:

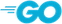	Precedence	Associativity	Arity	Fixity
+ - ! ^ * & <-	Highest		1	Prefix
* / % << >> & &^	5	L	2	Infix
+ - | ^	4	L	2	Infix
< <= == != >= >	3	L	2	Infix
&&	2	L	2	Infix
||	1	L	2	Infix

Advice

Oh, and there is always this old bit of advice: When it doubt, just use lots of parentheses.

Evaluation Order

When there are subexpressions in a complex expression, must certain subexpressions be evaluated before others? Or can they be evaluated in an arbitrary order? Or even in parallel? Would it even matter?

Defined Order

Java forces a left-to-right ordering: a-f(b)-c*d means do the following, one after another:

Undefined Order

Most languages allow the evaluation order to be undefined so that the compiler can choose the best order it can. This is especially important for parallel architectures (multiprocessor or multicore).

For example, a–f(b)–c*d can be parallelized as

Also, a:=b[i]; c:=a*2+d*3 can be done like this:

Undefined ordering can lead to ambiguities or errors:

• Suppose g were a function which modified the global variable a as a side effect. Then the expression f(a,g(b)) could yield different results depending on which order the arguments were evaluated.
• One might be tempted to do these two statements a:=b; c:=d in parallel, but if a and d are aliases of each other we can’t.
• In languages that do saturated arithmetic or throw exceptions on arithmetic overflow, (a+b)-c might behave very differently from (a-c)+b, so a compiler shouldn’t rearrange operands unless it understands these semantics.

$ swift
  1> let a: Int8 = 100
let a: Int8 = 100
  2> let b: Int8 = 50
b: Int8 = 50
  3> let c: Int8 = 40
c: Int8 = 40
  4> (a - c) + b
$R0: Int8 = 110
  5> (a + b) - c
Execution interrupted. Enter code to recover and continue.
Enter LLDB commands to investigate (type :help for assistance.)

Short-Circuit Operators

Sometimes the order goes like this: evaluate the left-most operand, then, only if necessary, evaluate the second. You may not even need to evaluate the second at all.

Short-circuiting appears frequently in many programming idioms

• Null pointer check:

  if (p != null && p.key == value) { ... }
  

• Simulating a “default” parameter:

  function f(x, y) {
      // You *can* do this, but JS has default arguments so use those!
      y ??= 1;
      ...
  }
  

• If something fails, take another action:

  open(F, $file) or die "Can’t open $file: $!";
  

• Continue with a second action only if something succeeds

  exists f && remove f
  

Conditional Evaluation

Sometimes the order goes like this: evaluate a designated operand, known as the test, or condition, first. Then depending on the result, evaluate exactly one of the remaining operands, leaving the result unevaluated.

This expression is written in a lot of different ways:

The short-circuit operators we saw above can be written with conditional operators. Note:

• x && y can be written as x ? y : x
• x || y can be written as x ? x : y

This big idea here is that this conditional expression is not like a typical function call in C-like languages. If it were, it would look something like:

    if (test, consequent, alternative)

and in typical languages, all three operands would be evaluated. We want the test to be evaluated, and then only one of the remaining operands to be evaluated, not both.

We’ll see more conditional evaluation and execution in our notes on control flow.

This is a pretty neat segue into our next topic.

Lazy Evaluation

If expressions are only evaluated as-needed, or on demand, or only-if-needed, evaluation is said to be lazy. Otherwise it’s eager.

def first(x, y):
    return x

first(f(), g())

Under eager evaluation, both f and g are called, and the results of each are passed to first. Under lazy evaluation, only f gets called. In our example, suppose f() evaluates to 3 and g() to 5. Then:

first(f(), g())
    = first(3, f())
    = first(3, 5)
    = 3

first(f(), g())
    = f()
    = 3

In the cases where g() crashes or has other side effects, the difference between the two strategies can be a big deal.

Side Effects

Note that evaluation order really only matters when side effects can occur (which is why immutability is preferred!). Side effects are what occurs when a storage location is updated or when files or a database are read from or written to.

Lvalues and Rvalues

Storage locations are denoted by lvalues. They are called lvalues because they can appear on the Left side of an assignment. Examples in C:

• x
• x[4]
• y[5].p()->q
• *(e1 + e2)
• *y[6]

An example of an rvalue is 500 (an integer literal).

Sometimes pretty complicated looking expressions can evaluate to lvalues! Examples:

// C++, but not C
(x *= 10) += 7

($x < 5 ? $y : $z) = 10;

$x = "dog";
${$x} = 2;
$x = <STDIN>
chomp $x;
${$x} = 2;

val x = ref 0;
x := 3;
x := !x + 1;

Sometimes, lvalues can be made read-only. Examples:

• Variables marked const in C, let in Swift, val in Kotlin, or final in Java.
• for-loop indices and in-parameters in Ada
• Variables outside of a function in Euclid and Turing

Sometimes, immutability is the default, and you have to add keywords or symbols to make an lvalue mutable.

Macros

A macro is code that gets expanded into new code which then gets compiled and run. In the simplest case, a macro gets expanded into source code, as in this example in C:

#define area(r) (M_PI*(r)*(r))
double f(x) {
    return 3 / area(x+10);
}

but before the program is compiled, the C preprocessor expands the macro, producing:

double f(x) {
    return 3 / (M_PI*(x+10)*(x+10));
}

    #define area(r) M_PI*r*r;

More examples of C macros:

#define MAX(x, y) ((x) > (y) ? (x) : (y))

#define mientras while

#define forever while(1)

C macros operate in source code. The macros of Lisp, Clojure, and Julia are much more sophisticated: these operate on abstract syntax trees. We’ll cover these when we get to metaprogramming.

Comptime

Several languages allow you to write code that is evaluated at compile time. Zig even uses the keyword comptime. Others have different syntactic forms.

Bonus: A Bunch of Operators

For no good, reason, here’s a bunch of operators, together with their renderings from a few programming languages. Please don’t assume this list is ordered in any particular way or that it is anywhere near complete.

Unary Operators

Binary Operators

Ternary Operators

Sure, it can be confusing that one symbol and mean one thing in one language and something completely different in another. This is a good reason to learn the concepts and the vocabulary. Don’t think in terms of the symbols. Think in terms of the concepts.

Recall Practice

Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.

1. An expression is an entity made from applying _________________ to ________________.
   operators, operands
2. What are four syntactic attributes of operators?
   precedence, associativity, arity, fixity
3. What is operator precedence? What does is mean for operator O1 to have higher precedence than operator O2? Give a precise example.
4. What is operator associativity? What does is mean for an operator to be left associative? Right associative? Non associative? Give precise examples for each.
5. Evaluate, if possible, the expression in -2**2 in JavaScript and Python. Explain why the evaluation produced the value it did in each language.
   In Python, it evaluates to 4 because the unary negation is applied after the exponentiation. In JavaScript, this is a syntax error, because Java wisely figures reasonable minds can disagree on the relative precedence of these operators, so it prohibits you from writing such things.
6. Why would a language define an evaluation order for expressions? Why would it choose to leave the evaluation order undefined?
   A defined order is good for language portability. An undefined order allows the compiler to choose the best order for performance, especially in parallel architectures.
7. How can the expressions a+(b-c) and (a+b)-c produce different results? (Assume $a$, $b$, and $c$ are simple variables holding integer values.)
   In languages in which overflow errors and panics, one may panic and the other may not.
8. What is a short-circuit operator?
   An operator that evaluates its second operand only if the first operand does not determine the result.
9. What are Lvalues and Rvalues?
   Lvalues are storage locations that can appear on the left side of an assignment. Rvalues are values that can appear on the right side of an assignment.
10. What does the following script output under lazy evaluation? Under eager evaluation? Assume arguments are evaluated from left to right.

      var x = 5
      function f() { return x = x * 3 }
      function g() { return x = x * 5 }
      function h(a, b) { return a + x }
      print(h(f(), g()))
    

    Eager: 90, Lazy: 30
11. What is comptime?
    A feature in some programming languages that allows certain expressions to be evaluated at compile time rather than at runtime.
12. How is a macro different from a function?
    A macro is expanded into source code before compilation, while a function is called at runtime.
13. What is an expression-oriented language?
    One in which every (or nearly every) construct we think of as a statement, such as an assignment, block, if, or while, is actually an expression.

Summary