Haskell

Why Haskell?
You’ll want to learn Haskell because it is:
- a pure functional language i.e., functions have no side effects (Technically: the few that do, e.g. I/O, current time, random numbers, etc., are strictly isolated and can NOT pollute the rest of the code);
- statically-typed, i.e., the types of all expressions are checked before the program runs; and
- lazy, i.e., expressions are not evaluated until (and unless) they are needed.
What’s the big deal about a pure functional language?
With no side effects, and with referential transparency, your code is:
- Thread-safe
- Anemable to more compiler optimizations
- Easier to prove correct
- Often more reusable
- Easier to implement on massively parallel platforms such as multicore architectures or computing clusters
Haskell is arguably part of the amazing ML family of languages. This family includes the original ML, Standard ML, OCaml, Lazy ML, F#, Hope, Miranda, Elm, and PureScript. (Some may consider only the first six true ML languages, with the latter four plus Haskell simply ML derivatives.)
But doe anyone care? Well yeah, that’s the joke. There’s a famous snarky and satirical article about that. Haskell also has this reputation as being used by cult members, and of being an ivory tower language (a myth this article tries to debunk).
Jeff’s intro mentions places it indeed is used:
Actually, a lot of companies use it.
Getting Started
Like most languages, you can play with Haskell on repl.it, jdoodle, Try it Online, or other online coding sites. Or, you can install a Haskell compiler on your own machine: GHC is the most popular. It comes with a compiler, a REPL, and access to tons of third-party packages through Hackage.
The REPL
Install GHC, then let’s begin with its REPL (it’s called ghci):
$ ghci GHCi, version 8.4.3: http://www.haskell.org/ghc/ :? for help Prelude> 3 + 99 * 2 201 Prelude> (3 - 2) ** 20 / 2 0.5 Prelude> succ 22 23 Prelude> min 5 3 3 Prelude> head [8, 9, 2, 3] 8 Prelude> tail [8, 9, 2, 3] [9, 2, 3] Prelude> not (False || True && (9 /= 5)) False Prelude> "dog" ++ "house" "doghouse" Prelude> "dog" == "dog" True Prelude> [2, 3, 5] == [2, 3, 5] True
Ooh, three interesting things:
- Function calls don’t use parentheses
- string concatenation uses
++(you don’t get confused with+), and - list equality is by-value, as in Python, WOOHOO!
In the REPL, you can create bindings (note the word “binding”, NOT “assignment”):
Prelude> dozen = 12 Prelude> dozen * 6 72 Prelude> plusTwo = \x -> x + 2 Prelude> plusTwo 99 101 Prelude> plusTwo 99 * 5 505 Prelude> plusTwo (99 * 5) 497 Prelude> plusTwo $ 99 * 5 497 Prelude> plusTen x = x + 10 Prelude> plusTen 45 55
Note that prefix operators bind more tightly than infix operators. It’s possible to use infixes in prefix position, and prefix “binary” operators in infix position:
Prelude> 5 + 8 -- plus is an infix operator 13 Prelude> (+) 5 8 -- Use parens to make an infix a prefix 13 Prelude> min 21 55 -- min is a prefix operator 21 Prelude> 21 `min` 55 -- Use backticks to make a prefix an infix 21
$ operator. That’s pretty cool, no?
Programs in Files
Now let’s put a program in a file and compile and run it. Save the following as hello.hs:
main = putStrLn("Hello, world")
The GHC compiler produces the intermediate files hello.hi and hello.o, as well as the executable hello (these file names might differ on Windows—you’re on your own to figure those out if you use Windows). Compile and execute together like this:
$ ghc hello.hs && ./hello Hello, world
More scripts, please:
-- The program reads a line from standard input, so if you run
-- it on the command line, it will stop and wait for you to
-- type something in.
main =
getLine >>= \s -> putStrLn $ "Hello, " ++ s
primes = filterPrime [2..]
where
filterPrime (p:xs) =
p : filterPrime [x | x <- xs, x `mod` p /= 0]
main = print (take 10 primes)
quickSort :: (Ord a) => [a] -> [a]
quickSort [] = []
quickSort (x:xs) = quickSort [a | a <- xs, a < x]
++ [x] ++
quickSort [a | a <- xs, a >= x]
main =
print $ (quickSort [5,3,4,1,2,6] == [1..6]) || error("fail")
Okaaaaaaaaaay, Haskell’s got some weird symbols in there. We better back off and learn some basics before we get too deep!
The Basic Types
Here are the most basic six types from the Prelude (the built-ins, so to speak):
| Type | Description | Examples |
|---|---|---|
| Int | Fixed-precision integer | 300
|
| Integer | Arbitrary-precision integer | 3898995532122312399129919231231111
|
| Float | Single-precision floating-point number | 9.9 |
| Double | Double-precision floating-point number | -3.897E307 |
| Bool | A truth values | True False
|
| Char | A unicode character | 'E' 'π' '\n' '\t' '\\' '\x1f4a9' '😰'
|
If you need complex numbers and rational numbers (ratios), they are in another library. More on this later.
0.1 + 0.2 in the REPL.
The REPL command :t will tell you the type of an expression.
Prelude> :t '%' Char Prelude> :t -10 < -5 Bool
Tuple, List, and Function Types
Examples of tuple types: (Bool, Char), (Char, Bool), and (Int, (Int, Char), Double, Int). These are distinct types. Each different tuple type has a fixed size. Its component types can be anything at all: Tuples are heterogeneous.
Prelude> :t (True, 'ü')
(Bool, Char)
Prelude> :t ('z', False, False)
(Char, Bool, Bool)
Prelude> :t ()
()
Examples of list types: [Int], [Char], [[Int]], [(Char, [Char])]. All list components must be of the same type: they are homogeneous. The length of the list is not part of its size.
Prelude> :t [False, True, True, False] [Bool] Prelude> :t ['d', 'o', 'g'] [Char] Prelude> :t "dog" [Char] Prelude> :t [[False, False], [True], []] [[Bool]]
Woah! STRINGS ARE JUST LISTS OF CHARACTERS! Who knew?! At least Haskell lets us write them with double quotes.
A function type is composed from a single input type and a single output type. There is no such thing as a function taking in multiple arguments: All functions take exactly ONE argument. You can simulate multiple arguments by having the input type be a tuple type, or by making the output be a function (something called currying, which you might already know....)
Example function types: Bool -> Bool, Int -> [Char], (Integer, Integer) -> Integer, and Int -> (Int -> Bool). The arrow is right-associative so we can write the last example there as just Int -> Int -> Bool.
Prelude> :t \c -> c == '💁' Char -> Bool Prelude> :t \s -> s ++ "ee" [Char] -> [Char] Prelude> :t \x -> (x::Integer) < 100 Integer -> Bool Prelude> :t \(x, y) -> (y::Int) - x (Int, Int) -> Int Prelude> :t \x -> \y -> (y::Int) - x Int -> Int -> Int
As you might have guessed, the :: forces an expression to have a particular type.
Type Variables
We know [Char] and [Float] are two different types. So how do we speak about, or write functions that work on, lists of ANY type? Or tuples of any size, or any component type?
Answer: type variables. Type variables come in lowercase. Examples:
Prelude> :t \(x, y) -> y (a, b) -> b Prelude> :t \(x, y) -> head y (a, [b]) -> b Prelude> :t \x -> \y -> \z -> (x, y) a -> b -> c -> (a, b) Prelude> :t \x -> \y -> \z -> (x, \w -> not y) a -> Bool -> b -> (a, c -> Bool)
Now the following table should make sense:
| Type | Description |
|---|---|
[a] | The type of lists of type a
|
(a,b) | The type of two-tuples where the first element has type a and the second has type b
|
(a,b,c) | The type of three-tuples .... |
() | Apparently the type of tuples with zero elements. If you think about it, there is only ONE value of this type. So it is called the unit type. Oddly enough, this technically isn’t a tuple type; see the official docs for details. |
| a -> b | The type of functions from type a to type b.
|
three such that three () == 3.
Typeclasses
What is the type of the expression 21? Is it Int, Integer, Float, or Double? That’s a tough one!
How about a type variable? Well, the variable cannot stand for ANY type, just one of those four. We need constrained type variables—something like a | a ∈ {Int, Integer, Float, Double}.
And what about the type of \x -> x / 2? Is it just a -> a | a ∈ {Float, Double} or perhaps a | a is any type for which (/)::a->a->a exists?
Haskell’s solution is typeclasses. Types that share bits of behavior are instances of the same typeclass. Typeclasses live in a hierarchy. Here are some of the built-in typeclasses, shown with the functions they define:
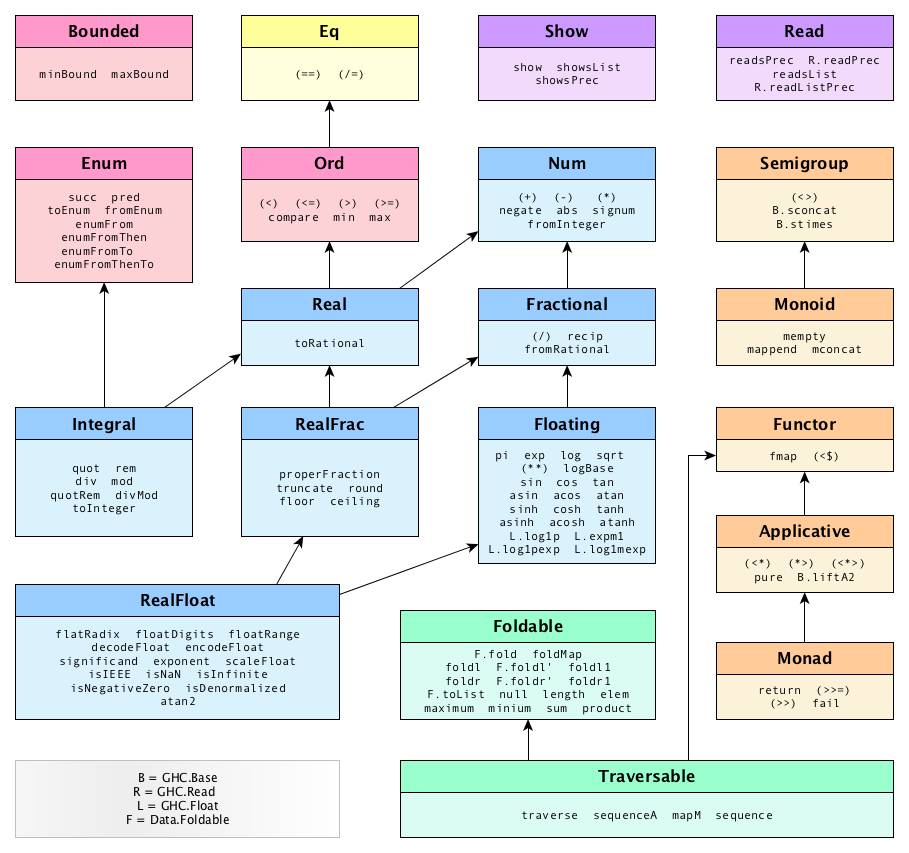
Havig a hierarchy means that any type which is an instance of Integral, for example, is also an instance of Real, Num, Ord, and Eq. A type can belong to many typeclasses. Here’s a list of some types and the typeclasses that they are instances of:
| Type | Typeclasses |
|---|---|
| Bool | Eq, Ord, Show, Read, Enum, Bounded |
| Char | Eq, Ord, Show, Read, Enum, Bounded |
| Int | Eq, Ord, Show, Read, Enum, Bounded, Num, Real, Integral |
| Integer | Eq, Ord, Show, Read, Enum, Num, Real, Integral |
| Float | Eq, Ord, Show, Read, Enum, Num, Real, Fractional, RealFrac, Floating, RealFloat |
| Double | Eq, Ord, Show, Read, Enum, Num, Real, Fractional, RealFrac, Floating, RealFloat |
| Word | Eq, Ord, Show, Read, Enum, Bounded, Num, Real, Integral |
| Ordering | Eq, Ord, Show, Read, Enum, Bounded, Semigroup, Monoid |
| () | Eq, Ord, Show, Read, Enum, Bounded, Semigroup, Monoid |
| Maybe a | Eq, Ord, Show, Read, Semigroup, Monoid, Functor, Applicative, Monad, Foldable, Traversable |
| [a] | Eq, Ord, Show, Read, Semigroup, Monoid, Functor, Applicative, Monad, Foldable, Traversable |
| (a,b) | Eq, Ord, Show, Read, Bounded, Semigroup, Monoid, Functor, Applicative, Monad, Foldable, Traversable |
| a->b | Semigroup, Monoid, Functor, Applicative, Monad |
| IO | Semigroup, Monoid, Functor, Applicative, Monad |
| IOError | Eq, Show |
You can glean a lot of interesting information based on what typeclasses a type does not implement.
- Functions and IO objects can NOT be tested for equality, nor can they be compared, printed, or read. (Function equality is undecidable in general, did you know?)
- IOErrors can be tested for equality and printed, but not compared or read.
- Bools, Chars, and Ints are bounded (have a minimum value and maxium value), but Integers, Floats, and Doubles, do not.
- It makes sense to fold and traverse lists and tuples, but not much else (though you can create new types and add them to typeclasses, as we’ll soon see.)
Type variables can be constrained to typeclasses. So we can say “The type of 21 is a, where the type variable a must be an instance of the typeclass Num.” Haskell shows subclass constraints on the left of the => symbol in the type. Examples:
Prelude> :t 21 Num p => p Prelude> :t 9.0001 Fractional p => p Prelude> :t min Ord a => a -> a -> a Prelude> :t succ Enum a => a -> a Prelude> :t \(x, y) -> tan x < 5 || y (Ord a, Floating a) => (a, Bool) -> Bool Prelude> :t \n -> succ n == 8 (Eq a, Enum a, Num a) => a -> Bool Prelude> :t \x -> \y -> \z -> (y, z, x - 1) Num c => c -> a -> b -> (a, b, c) Prelude> :t \x -> \y -> (y > y, x / 2.5) (Ord a, Fractional b) => b -> a -> (Bool, b)
Type Signatures
Have you noticed that Haskell does way better type inference than Go, Rust, Swift, Java, C++, C#, and many other statically-typed languages? But even though Haskell can infer almost all types, it’s considered good practice to put type signatures on all of your top-level declarations. Example:
feigenbaumConstant :: Double feigenbaumConstant = 4.669201609102990 tripleToList :: (a,a,a) -> [a] tripleToList (x,y,z) = [x,y,z] isIncreasingTuple :: (Ord a) => (a, a) -> Bool isIncreasingTuple (x, y) = x < y advance :: (Eq a, Bounded a, Enum a) => a -> a advance x = if x == maxBound then minBound else succ x
Why should you use type signatures?
- It adds beautiful documentation.
- The inferred type might be more general than you want.
- The automatic inferencer might be buggy or underpowered.
- The problem of inferring higher-order types is undecidable in general.
Back to Programming, For a Bit
We’re getting too deep again. Let’s back out for a bit and look at how to actually do productive work in Haskell.
In addition to creating bindings and evaluating expressions with function calls, there are some other syntactic forms of expressions:
Prelude> 89::Integer -- type qualification 89 Prelude> let x = 10 in x * x -- let expression 100 Prelude> let x = 2 ; y = 3 in y * x + 1 -- let expression 7 Prelude> if 8 < 5 then 2 else 21 -- if expression 21
Numbers
Let’s play with some functions on numbers:
Prelude> logBase 2 1024 10.0 Prelude> floor 8.75 8 Prelude> floor (-8.75) -- without the parens, parses as floor minus 8.75 -9 Prelude> recip 2 0.5 Prelude> isInfinite $ sqrt pi -- same as isInfinite (sqrt pi) False Prelude> sin (pi / 2) 1.0 Prelude> [round 0.5, round 1.5, round 2.5, round 3.5] [0,2,2,4] Prelude> 98 `divMod` 25 (3,23) Prelude> 98 `quotRem` 25 (3,23) Prelude> gcd 4710963 55187 5017
quot and div, and between rem and mod. Explain the difference in words.
trunc, round, floor, and ceiling. How does round behave at the midpoint between two integers?
Functions
Functions are totally first-class in Haskell, so all the cool stuff regarding higher-order functions, closures, and currying is front-and-center, and very natural, in Haskell.
Currying
Curried functions are the preferred style in Haskell. Uncurried functions are those
Prelude> add (x, y) = x + y Prelude> add (5, 8) 13 Prelude> add x y = x + y Prelude> add 5 8 13 Prelude> (add 5) 8 13 Prelude> plusFive = add 5 Prelude> plusFive 8 13 Prelude> map (add 5) [1..10] [6,7,8,9,10,11,12,13,14,15]
curry and uncurry and provide examples of their use.
Closures
Notice that each of these three definitions are equivalent:
add x y = x + y
add x = \y -> x + y
add = \x -> \y -> x + y
The last two notations really show off closures. The function \y -> x + y has a bound variable y and a free variable x. A closure is a function with a free variable that takes its value from the surrounding environment. The function returned by add x is a closure, since it carries around the value of x.
Closures arise naturally from curried functions.
But you will not see in Haskell closures used the way they are frequently used in JavaScript—to implement generators or to maintain state. Haskell has lazy infinite lists, and in the rare cases you need state, has a state monad. More on these later.
Operator Sections
Infix operators in parentheses are just like any other curried two-argument function:
3 < 5 ⟹ True
(<) 3 5 ⟹ True
((<) 3) 5 ⟹ True
So the function ((<) 3) when applied to an argument x, returns whether 3 is less than x. Now, if you leave off the parens around the infix operator, you can create a section. There are two kinds:
(<3) ⟺ \x -> x < 3 -- a right section
(3<) ⟺ \x -> 3 < x -- a left section
Using sections, you can define functions without variables, for example:
twoToThe = (2**) halfOf = (/2) oneOver = (1/) isZero = (==0) onePlus = (1+)
(>=0), (`mod` 2), (0-), and (++"s").
Higher-Order Functions
There are some neat built-in functions and operators that take functions as arguments or return functions.
(f . g) x ⟹ f (g x)
(flip f) x y ⟹ f y x
(curry f) x y ⟹ f (x, y)
(uncurry f)(x, y) ⟹ f x y
Examples:
Prelude> (recip . succ) 7 0.125 Prelude> ((+3) . (2^)) 3 11 Prelude> ((2^) . (+3)) 3 64 Prelude> (uncurry min)(9, 5) 5 Prelude> flip (^) 10 2 1024
And of course, you can write your own:
twice f x = f (f x)
twice to use the function composition operator (.).
Let-expressions
That let is nice and readable, but you know, it’s actually not necessary. After all,
let x = E1 in E2
is really just
(\x -> E2)(E1)
For example:
let x = 7 * 3 in 100 + x ⇒ (\x -> 100 + x)(7 * 3) ⇒ 100 + (7 * 3)
Lists
Check out some different ways to make lists. Haskell has ranges and comprehensions:
Prelude> [5..8] [5,6,7,8] Prelude> [0,3..21] [0,3,6,9,12,15,18,21] Prelude> [x ** 2 | x <- [0..10]] [0.0,1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0,100.0] Prelude> [x | x <- [0..30], x `mod` 3 /= 0 && x `mod` 5 /= 0] [1,2,4,7,8,11,13,14,16,17,19,22,23,26,28,29] Prelude> [(x, y) | x <- [0..3], y <- "ab"] [(0,'a'),(0,'b'),(1,'a'),(1,'b'),(2,'a'),(2,'b'),(3,'a'),(3,'b')] Prelude> replicate 3 "dog" ["dog","dog","dog"]
Here are some examples of basic list functions:
null [] ⟹ True
null [3,5,8,2,1] ⟹ False
head [3,5,8,2,1] ⟹ 3
tail [3,5,8,2,1] ⟹ [5,8,2,1]
init [3,5,8,2,1] ⟹ [3,5,8,2]
last [3,5,8,2,1] ⟹ 1
length [3,5,8,2,1] ⟹ 5
take 2 [3,5,8,2,1] ⟹ [3,5]
drop 2 [3,5,8,2,1] ⟹ [8,2,1]
takeWhile (\x -> x < 7) [3,5,8,2,1] ⟹ [3,5]
takeWhile (< 7) [3,5,8,2,1] ⟹ [3,5]
dropWhile (not . even) [3,5,8,2,1] ⟹ [8,2,1]
filter (< 7) [3,5,8,2,1] ⟹ [3,5,2,1]
filter even [1..10] ⟹ [2,4,6,8,10]
map succ [3,5,8,2,1] ⟹ [4,9,6,3,2]
map (2^) [3,5,8,2,1] ⟹ [8,32,256,4,2]
splitAt 3 [3,5,8,2,1] ⟹ ([3,5,8],[2,1])
zip [1,2] ['a','b'] ⟹ [(1,'a'),(2,'b')]
concat [[3],[5,8],[],[2,1]] ⟹ [3,5,8,2,1]
concatMap (\x -> [x,-x]) [1..5] ⟹ [1,-1,2,-2,3,-3,4,-4,5,-5]
all even [3,5,8,2,1] ⟹ False
any even [3,5,8,2,1] ⟹ True
sum [1..10] ⟹ 55
product [1..10] ⟹ 3628800
foldl (-) 1 [3,5,2,8] ⟹ -17
foldr (-) 1 [3,5,2,8] ⟹ -7
foldl is fold left, foldr is fold right. Here is how they work:foldl (-) 1 [3,5,2,8] ⟹ ((((1-3)-5)-2)-8)foldr (-) 1 [3,5,2,8] ⟹ (3-(5-(2-(8-1))))Learn more about folds.
foldl? (Hint)
A list is formally defined as being either [] (empty) or an element consed (with the infix `:` operator) to the front of a list.
Prelude> [] [] Prelude> 3 : [] [3] Prelude> 3 : 5 : [] [3,5] Prelude> 2 : 3 : 5 : [] [2,3,5] Prelude> 5 : [6..8] [5,6,7,8]
: operator is pronounced “cons”.
In general, when you define functions on a constructed type, like lists, always use pattern matching on its constructors, and avoid using the extractor functions. For example:
-- DO NOT WRITE LIST FUNCTIONS LIKE THIS. THIS WORKS BUT IS NOT PREFERRED. stutter xs = if null xs then [] else (head xs):(head xs):(stutter (tail xs)) -- WRITE THEM LIKE THIS INSTEAD. THIS WAY IS GOOD. stutter [] = [] stutter (x:xs) = x:x:(stutter xs)
We’ll see more pattern matching soon.
There are tons more cool functions on lists, by the way. Many of them are in the module Data.List, which you need to import. In the REPL, for example:
Prelude> permutations [1,2,3]
error: Variable not in scope: permutations :: [Integer] -> t
Prelude> import Data.List
Prelude Data.List> permutations [1,2,3]
[[1,2,3],[2,1,3],[3,2,1],[2,3,1],[3,1,2],[1,3,2]]
Data.List is a standard module that comes with your Haskell distribution. There are hundreds of functions in it. You should browse the complete documentation now. You should see over 100 functions. Read the docs!
Now, you may have noticed: Prelude is a module also. See the docs. See the source. Notice how the Prelude module imports a bunch of other modules, but selectively exports only some of the functions in each!
Laziness, and Infinite Lists
It is time to talk about what it means that Haskell is lazy. This REPL session will hopefully convey the idea:
Prelude> head [] *** Exception: Prelude.head: empty list Prelude> x = head [] -- No error! Prelude> t = (5, x) -- No error here either! Prelude> fst t -- Nor here! 5 Prelude> snd t *** Exception: Prelude.head: empty list
Lazy evaluation means expressions are only evaluated when needed. The opposite is strict evaluation. With strict evaluation, all tuple values would be evaluated when the tuple was first defined. And all list elements would be evaluated when a list was defined. And all function arguments would be evaluated before the function was called.
Prelude> x = [5, head [], 10] Prelude> (\x -> \y -> x) "good" (head []) "good"
Now since list elements are not needed until used, WE CAN MAKE INFINITE LISTS!
Prelude> positives = [1..] Prelude> nonNegativeEvens = [0,2..] Prelude> ones = repeat 1 Prelude> turns = cycle [0..4] Prelude> take 10 positives [1,2,3,4,5,6,7,8,9,10] Prelude> take 10 nonNegativeEvens [0,2,4,6,8,10,12,14,16,18] Prelude> takeWhile (<30) nonNegativeEvens [0,2,4,6,8,10,12,14,16,18,20,22,24,26,28] Prelude> take 5 ones [1,1,1,1,1] Prelude> take 18 turns [0,1,2,3,4,0,1,2,3,4,0,1,2,3,4,0,1,2] Prelude> 7 `elem` positives True Prelude> nonNegativeEvens !! 17 34 Prelude> import Data.List Prelude Data.List> [0,1,2] `isPrefixOf` turns True Prelude Data.List> [0,1,2] `isPrefixOf` ones False Prelude Data.List> map (1+) positives !! 9 11
If you try to print an infinite list, or look for an element that’s not there, or other such things, your program will enter an infinite loop.
Characters
The moduleData.Char contains lots of good stuff. Examples:
isDigit 'x' ⟹ False
isLetter 'é' ⟹ True
isSymbol '👠' ⟹ True
isSymbol '€' ⟹ True
isLetter '👠' ⟹ False
isLetter 'ま' ⟹ True
toUpper 'ø' ⟹ 'Ø'
toLower 'B' ⟹ 'b'
ord 'A' ⟹ 65
ord '👠' ⟹ 128096
chr 0x1f4a9 ⟹ '💩'
Strings
Strings are lists, so everything you can do on a list of arbitrary type you can do on a string. Import Data.List and Data.Char and have fun:
null "" ⟹ True
null "hello" ⟹ False
head "hello" ⟹ 'h'
tail "hello" ⟹ "ello"
init "hello" ⟹ "hell"
last "hello" ⟹ 'o'
length "café" ⟹ 4
length "👠👠👠" ⟹ 3
map toUpper "scream" ⟹ "SCREAM"
intersperse '-' "SHOWTIME" ⟹ "S-H-O-W-T-I-M-E"
intercalate " & " ["swim","run","bike"] ⟹ "swim & run & bike"
transpose ["too","urn","bee"] ⟹ ["tub","ore","one"]
subsequences "abc" ⟹ ["","a","b","ab","c","ac","bc","abc"]
permutations "abc" ⟹ ["abc","bac","cba","bca","cab","acb"]
concat ["dog", "house", "s"] ⟹ "doghouses"
concatMap reverse ["dog", "house", "s"] ⟹ "godesuohs"
take 5 (repeat 'x') ⟹ "xxxxx"
replicate 5 'x' ⟹ "xxxxx"
replicate 3 "ho" ⟹ ["ho","ho","ho"]
(concat . replicate 3) "ho" ⟹ "hohoho"
(intercalate " " . replicate 3) "ho" ⟹ "ho ho ho"
isPrefixOf "car" "carpet" ⟹ True
isSuffixOf "car" "carpet" ⟹ False
isInfixOf "Java" "Use JavaScript" ⟹ True
isSubsequenceOf "Satan" "Ship a tarp now" ⟹ True
elem 'o' "DOG" ⟹ False
elem 'O' "DOG" ⟹ True
filter isLetter "19. José 1988 3π" ⟹ "Joséπ"
partition isLetter "19. José 1988 3π" ⟹ ("Joséπ", "19. 1988 3")
"abcdef" !! 4 ⟹ 'e'
elemIndex 'b' "abracadabra" ⟹ Just 1
elemIndex 'e' "abracadabra" ⟹ Nothing
elemIndices 'b' "abracadabra" ⟹ [1,8]
elemIndices 'e' "abracadabra" ⟹ []
sort "9v[ajecni" ⟹ "9[aceijnv"
lines "one\n two \n\n3" ⟹ ["one"," two ","","3"]
Tuples
Tuples are simple creatures. We’ve seen that the type (a,b) is the type of all pairs where the first element is of type a and the second of type b. What can we do with tuples? Not a whole lot! In fact, here is the entire Data.Tuple module (minus comments and other metadata-ish things):
module Data.Tuple ( fst , snd , curry , uncurry , swap ) where fst :: (a,b) -> a fst (x,_) = x snd :: (a,b) -> b snd (_,y) = y curry :: ((a, b) -> c) -> a -> b -> c curry f x y = f (x, y) uncurry :: (a -> b -> c) -> ((a, b) -> c) uncurry f p = f (fst p) (snd p) swap :: (a,b) -> (b,a) swap (a,b) = (b,a)
The Prelude module imports Data.Tuple then exports all of the tuple functions except swap.
reflectAbout45DegreeLine that takes a polygon represented as a list of 2-Tuples and returns the list of all those pairs with their coordinates swapped. Include a type signature. Use map from Data.List and swap from Data.Tuple.
Pattern Matching
Whenever you have a type that is constructed, as lists are with (:), and tuples are with (,), and Booleans (data Bool = True | False) and integers (conceptually it’s as if it is data Int = ... | -2 | -1 | 0 | 1 | 2 | ...), then you can use a case expression on the constructors, instead of having nested if-expressions. Some contrived examples:
main :: IO()
main = do
putStrLn "Enter a number:"
line <- getLine
let num = (read line)::Int
response = case num of
12 -> "That is a dozen"
8 -> "Number of bits in an octet"
137 -> "I heard that was interesting"
-1 -> "i squared"
otherwise -> "thank you"
in
putStrLn response
Haskell has one awesome bit of syntactic sugar: If the entire body of a function is a single case expression, then you can define the function with the patterns:
third :: (a,b,c) -> c third (_, _, z) = z firstTwoEqual :: (Eq a) => [a] -> Bool firstTwoEqual [] = False firstTwoEqual [x] = False firstTwoEqual (x:y:_) = x == y isSeven :: (Integral a) => a -> Bool isSeven 7 = True isSeven _ = False
These work because the clauses are run in order, until one matches the arguments.
If there is no case in a match, you get a runtime error.
Prelude> second (x:y:_) = y
Prelude> second [1,2,3]
2
Prelude> second [1]
*** Exception: Non-exhaustive patterns in function second
Guards
Patterns use the constructors of a type. Guards test the values of expressions in order, until one of them matches. Again, better than nested if-expressions. Here’s a classic example:
grade :: (Num a, Ord a) => a -> [Char]
grade score
| score >= 90 = "A"
| score >= 80 = "B"
| score >= 70 = "C"
| score >= 60 = "D"
| otherwise = "F"
Maybe and Either
Sometimes when you evaluate an expression thing just don't make any sense, so the evaluation generates an error. (There is technically a difference between errors and exceptions that we aren’t covering in these notes.)
Prelude> head [] *** Exception: Prelude.head: empty list Prelude> ["dog","rat","bat"] !! (-1) *** Exception: Prelude.!!: negative index
Clearly these operations make no sense. But what if you are trying to find the index of an item in the list? It may or may not be there. It’s not an error if it’s not there, becuase you don’t know if it is or not. If it’s present, you want the index; if not, what do you want? Not an error, just a nice indication that it’s not there. This is what the type Maybe a helps with:
elemIndex 'b' "abracadabra" ⟹ Just 1
elemIndex 'e' "abracadabra" ⟹ Nothing
stripPrefix "dog" "doghouse" ⟹ Just "dog"
stripPrefix "dog" "cat" ⟹ Nothing
lookup "two" [("one","uno"),("two","dos")] ⟹ Just "dos"
lookup "eleven" [("one","uno"),("two","dos")] ⟹ Nothing
find even [3, 1, 8, 2, 10] ⟹ Just 8
find even [3, 1, 8, 2, 10] ⟹ Just Nothing
These functions have signatures
elemIndex :: Eq a => a -> [a] -> Maybe Int
Eq a => [a] -> [a] -> Maybe [a]
lookup :: Eq a => a -> [(a, b)] -> Maybe b
find :: Foldable t => (a -> Bool) -> t a -> Maybe a
You might notice that the Maybe type has constructors Just and Nothing so you should use pattern matching when dealing with them.
import Data.List
capitals :: [(String, String)]
capitals =
[ ("CA", "Sacramento")
, ("HI", "Honolulu")
, ("WA", "Olympia")
]
tellMeAbout :: String -> String
tellMeAbout state =
case (lookup state capitals) of
Just city -> "The capital of " ++ state ++ " is " ++ city
Nothing -> "I don't know anything about " ++ state
main :: IO ()
main = do
putStrLn $ tellMeAbout "HI"
putStrLn $ tellMeAbout "MA"
Maybes are a solution to the Billion Dollar Mistake
In Haskell, the only instances of typeStringare strings; there is no “null” or “nil” value of the type. In cases where a string value would be “optional,” you have the typeMaybe String.
If you would like to create a computation that might fail (instead of just not finding anything), you can use the Either a b type. In general, Either is used for a sum type, a type containing all values of two types. For example, the type Either String Int contains all the strings and all the ints, but only sort of, because all the values are tagged: sample values are Left "dog" and Right 5. Eithers are conventionally used for failable functions, with the left containing and error object or error message (your choice), and the right containing the successful result. Use pattern matching when dealing with these things.
Difference between Maybe and Either:
- Use
Maybe awhen you might have anaor you might not.- Use
Either a bfor the type containing allavalues and allbvalues. Good for when you expect a result of typebbut errors can occur, which are indicated by values of typea.
Data Types
It is time to move from the built-in types to defining our own.... So, how do we create our own types? Let’s start simply, in the REPL:
Prelude> data Light = RED | AMBER | GREEN Prelude> :t AMBER Light Prelude> show RED error: No instance for (Show Light) arising from a use of ‘show’ Prelude> RED == RED error: No instance for (Eq Light) arising from a use of ‘==’
At this point we probably want to put our mark our new type into the typeclasses Eq and Show. We ould then have to implement all the functions from that typeclass. Fortunately, we can use the deriving clause, which puts them in the typeclass and creates all right functions automatically.
Prelude> data Light = RED | AMBER | GREEN deriving (Eq, Show) Prelude> show RED "RED" Prelude> RED == RED True
The deriving clause only works for Eq, Ord, Enum, Bounded, Show, and Read.
Light datatype above to also belong to Ord, Bounded, and Enum. Validate your work by evaluating the expressions maxBound::Light, succ(RED), fromEnum GREEN, succ GREEN. What other expressions can you try?
Here’s another example:
data Shape
= Circle Double
| Rectangle Double Double
deriving (Eq, Show)
area :: Shape -> Double
area (Circle r) = pi * r * r
area (Rectangle h w) = h * w
perimeter :: Shape -> Double
perimeter (Circle r) = 2 * pi * r
perimeter (Rectangle h w) = 2 * (h + w)
main :: IO ()
main =
let
shapes = [Circle 10, Circle 1, Rectangle 7 2]
in
putStr $ unlines [show [area s, perimeter s] | s <- shapes]
From the command line:
$ ghc shapes.hs && ./shapes [314.1592653589793,62.83185307179586] [3.141592653589793,6.283185307179586] [14.0,18.0]
Let’s experiment in the REPL:
Prelude> :load shapes.hs Ok, one module loaded. *Main> c = Circle 20 *Main> area c 1256.6370614359173 *Main> area (Rectangle 20 30) 600.0 *Main> :t Circle -- Circle is a "constructor" Double -> Shape *Main> :t Rectangle -- Rectangle is a "constructor" Double -> Double -> Shape *Main> Rectangle 3 5 == Rectangle 3 5 True -- Yes we are an instance of Eq *Main> show (Rectangle 3 5) "Rectangle 3.0 5.0" -- Yes we are an instance of Show
Now it’s TREE TIME! 😛
Here’s a hacked together Binary Tree datatype, just to illustrate the use of a type variable in a data type. The code can use a bit of work. Later we’ll show how to put the type in its own module, and write a custom show function.
data Tree a = Empty | Node (Tree a) a (Tree a) deriving (Eq, Show)
size :: Tree a -> Int
size Empty = 0
size (Node left _ right) = size left + 1 + size right
preorder :: Tree a -> [a]
preorder Empty = []
preorder (Node left x right) = [x] ++ preorder left ++ preorder right
inorder :: Tree a -> [a]
inorder Empty = []
inorder (Node left x right) = inorder left ++ [x] ++ inorder right
main =
let
emptyTree = Empty::(Tree Int)
smallTree = Node Empty 8 (Node (Node Empty 7 Empty) 3 (Node Empty 5 Empty))
bigTree = Node smallTree 10 (Node smallTree 8 smallTree)
in do
print emptyTree
print smallTree
print bigTree
print $ size bigTree
print $ preorder smallTree
print $ inorder smallTree
ghc BinaryTree.hs && ./BinaryTree (or the equivalent on your operating system). Verify the output is as you expect.
Modules
We’ve used the built-in modules Data.List and Data.Tuple in the simplest way. We just imported them and were good to go; all of the exported entities in the module became available to our code. But certainly there is much to wonder about?
- If we are importing lots of modules, how might we avoid name clashes? Is there any way to mention the module name when referencing an entity? That might also add some readability, too.
- How do we create our own modules? We’d like to know both the syntax as well as where the modules go in the file system so they can be found on import.
The first question is easy: use import qualified:
Prelude> import qualified Data.List
Prelude Data.List> permutations "abc"
error:
• Variable not in scope: permutations :: [Char] -> t
• Perhaps you meant ‘Data.List.permutations’ (imported from Data.List)
Prelude Data.List> Data.List.permutations "abc"
["abc","bac","cba","bca","cab","acb"]
Prelude Data.List> import qualified Data.List as L
Prelude Data.List L> L.permutations "abc"
["abc","bac","cba","bca","cab","acb"]
Perhaps it is good to point out that the module Prelude is automatically imported into every Haskell source code file. Makes sense, right?
To answer the second question, let’s make a module for Binary Search Trees!
And while we’re at it, we’ll show how to add our new type to a typeclass using the instance keyword rather than the deriving keyword.
module BST
( Tree
, newTree
, insert
, size
) where
data Tree a = Empty | Node (Tree a) a (Tree a) deriving (Eq)
newTree :: Tree a
newTree = Empty
size :: Tree a -> Int
size Empty = 0
size (Node left _ right) = size left + 1 + size right
insert :: (Ord a) => a -> Tree a -> Tree a
insert x Empty = Node Empty x Empty
insert x (Node left y right)
| x == y = (Node left y right)
| x < y = (Node (insert x left) y right)
| otherwise = (Node left y (insert x right))
instance (Show a) => Show (Tree a) where
show Empty = "•"
show (Node left x right) =
"(" ++ (show left) ++ (show x) ++ (show right) ++ ")"
BST, it has to go in the file BST.hs. If the module were called Homework.MyCollections.BST then it would go in the file Homework/MyCollections/BST.hs.
Now let’s use the module:
import BST
main =
let
t1 = insert 3 $ insert 2 $ insert 13 $ insert 5 $ insert 8 newTree
t2 = insert 3 $ insert 2 $ insert 5 $ insert 13 $ insert 8 newTree
in do
print t1
print (size t1)
print (t1 == t2)
$ ghc test_BST.hs && ./test_BST [1 of 2] Compiling BST ( BST.hs, BST.o ) [2 of 2] Compiling Main ( test_BST.hs, test_BST.o ) Linking test_BST ... (((•2(•3•))5•)8(•13•)) 5 True
Check out the documentation for the basic libraries in GHC, containing all the standard modules.
Persistent Data Structures
You probably noticed that Haskell has no updating assignments. You can’t really mutate anything. Those let-expressions seem like they “assign” but they really just bind (once); you can’t change the binding to a new value.
So how do you add to a list? Insert into a tree? Remove an element from a set? Replace a value in a dictionary?
YOU DON’T! Add, delete, and update operations return a new data structure! You already knew this right? Look at some of these type signatures from the Data.List module:
reverse :: [a] -> [a]
take :: Int -> [a] -> [a]
drop :: Int -> [a] -> [a]
nub :: Eq a => [a] -> [a]
delete :: Eq a => a -> [a] -> [a]
If we return a new structure, the old one still hangs around; we have what are called persistent data structures. But is it efficient to keep the old ones around? What do you think happens here?
let
a = replicate 50 "dog"
b = "cat" : a
in
print (a, b)
Do you think we copy all the nodes of list a? Actually no, the (:) operator is efficient. This happens:
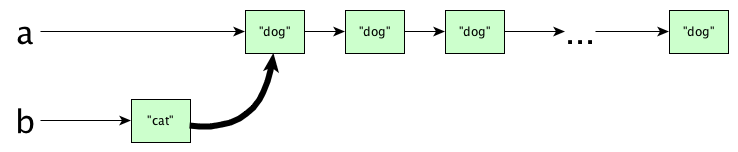
But, but, aren’t a and b sharing internal data? What would happen if we mutate a? Wouldn’t b get mutatated too? Isn’t this bad?
ANSWER: Calm down, you cannot mutate data structures. Since they are immutabale, this sharing is quite alright.
You do need to be aware of these inner workings, because efficiency matters. Consing to the front of a list is fine, but appending is a totally different story: if we had writtenb = a ++ ["cat"]then we would need an expensive copy...wereaorbever used (Gotta remember Haskell is lazy 😁).
Monads
Believe it or not, there’s a little scenario that, while pretty easy to understand, provides a good foundation into some deep programming theory that Haskell is known for. This little scenario is language independent, so let’s look at from different viewpoints. Here’s the problem:
Given the following types:
- Person, with a required name, optional address, and optional supervisor (who is a person)
- Address, with a required postal code, optional city, and optional indicator
- City, with a required name and optional population
Obtain the population of the city of the supervisor of a given person. Produce a null value if the data is not known.
Now, simply writing:
person.supervisor.address.city.population
will fail to type check or raise or throw a TypeError or NullPointerException if any of the optional fields are null. In languages without much compile-time type safety, such as Python, we need to write code to “check for nulls first” and write:
person.supervisor.city.population \
if person and \
person.supervisor and \
person.supervisor.address and \
person.supervisor.address.city \
else None

Haskell uses Maybe types to represent optional data. Here are the Haskell datatypes for our problem. Note it is a good time to introduce records:
data City = City { cityName :: String
, population :: Maybe Integer
} deriving (Eq, Show)
data Address = Address { postalCode :: String
, city :: Maybe City
, indicator :: Maybe String
} deriving (Eq, Show)
data Person = Person { name :: String
, address :: Maybe Address
, supervisor :: Maybe Person
} deriving (Eq, Show)
Now it’s certainly possible to solve our little problem with:
case person of
Nothing -> Nothing
Just person ->
case supervisor person of
Nothing -> Nothing
Just super ->
case address super of
Nothing -> Nothing
Just addr ->
case city addr of
Nothing -> Nothing
Just city -> population city
That seems necessary because each of the functions that produce maybe values have the form:
city :: Address -> Maybe String
but what we want is something like:
city' :: Maybe Address -> Maybe String
BUT GOOD NEWS! Maybe is an instance of the Monad typeclass, which has this amazing little (>>=) operator, which does exactly what we need! For Maybes, x >>= f produces Nothing when x is Nothing; otherwise it unwraps x from its Just wrapper and applies f. And it chains nicely. So we only have to write:
person >>= supervisor >>= address >>= city >>= population
Is there a big deal here?
Both Swift and Java can “chain” operations on optionals; Swift programmers can simply write:person?.supervisor?.address?.city?.population
BUT... This Swift operator (?.) works only on optionals; Haskell’s big idea is promoting the idea of returning a base value early and unwrapping/applying through a chain to the typeclass level. Any type that does this —Maybeis just of them — we call “a Monad.”Maybeis a Monad, and so are some other things, even lists, tuples, functions, and IOs.
A Monad, despite its funny name, just refers to a type that wraps values and can do the following:
return x: Wrap x (put x into the monad)x >>= f: Unwrap x and apply f to it (where f produces a wrapped value)The way these operations behave must follow some very simple rules in order to be universally applicable, but you get amazing benefits if you do:
- A great syntax for combining computations on fancy (wrapped) values
- Because lists are monads, a great syntax for cleanly representing computations of zero, one or more values
- A way to represent IO, which is impure, in such a way that this impureness cannot infect the pure parts of the program. How, you may ask? Well, as you’ll see: you can put values into the IO monad, but you can’t get them out.
return and >>= must follow) and explain why they are intutive in the case of Maybes and Lists.
Remember, “monad” is just a funny name for a way of combining computations that a good programmer like yourself would probably end up implementing anyway, simply by applying good programming practices like attempting to keep your code DRY. The nice thing Haskell does here is generalize the concept to the typeclass level, making it easier for you to take advantage of combining computations in your own types by defining only a very minimal set of likely intuitive behaviors. This is all awesome.
Purity, Side-Effects, and IO
So Haskell wants to be a pure functional language. What does this mean? Kris Jenkins explains it better than I can, so read Kris’s article now. Also read part two.
Hopefully you read the article(s). The TL;DR is that a pure function is one in which all implicit contextual inputs (side causes) become official arguments to a function, and any implicit outputs (side effects) become part of the offiical function return value. Something like:
myFunction :: (arg, context) -> (result, newContext)
Roughly speaking, if context contained a file stream, and myFunction read from it, then the return result would be whatever the function did with the head of the stream, and the returned context would be the tail of the stream.
In practice, we can represent this context by wrappers around values, in exactly the same way that Maybe values wrap present values in Just (and have the notion of an empty wrapper with Nothing). For example, IO values wrap the data read from and written to streams. And IO objects are Monads. Here are some basic functions:
getLine :: IO String
putStrLn :: String -> IO ()
print :: Show a => a -> IO ()
We can play with this in the REPL. If you use getLine in the REPL, you’ll have to type something in and hit Enter, of course.
Prelude> getLine >>= (putStrLn . ("You said " ++))
Hello world
You said Hello world
Prelude> print 1 >> print 2 >> print 3
1
2
3
(>>). Explain how this operator differs from (>>=).
There is a very popular do-syntax that works roughly like this:
| Unsugared Syntax | Sugared Syntax | ||
|---|---|---|---|
print 1 >> print 2 |
do
print 1
print 2
|
There’s much, much more to all this, but this should get you started.
getLine returns an IO String. Is there a way in Haskell to pass an IO String object to a function, unwrap the string from the IO, and operate on it, say, by returning its length? Why or why not? Write such a function if you can. If you cannot, point to the official language documentation that defines the prohibition on doing so (and, perhaps, its justification).
Summary
Haskell is pure.
- It does not have variables, assignments, or statements.
- No statements mean no for loops: navigate your structures recursively.
- Data structures are always immutable: operations on them return new ones.
- State, if needed, is handled through monadic structures and operations.
Haskell is lazy.
- We can have infinite lists. (Just don’t try to print them.)
- Usually this is more efficient, because we don’t execute what we don’t need.
- But there are times when it’s bad and strict is way better! We need to be careful.
Haskell is statically typed, with such good type inference, we don’t have to specify types.
- But generally, it’s a good idea to specify type annotations on our functions.
- Datatypes are so good; use them well so the compiler can check that you’ve covered everything.
How does Haskell do such a great job of type inference? It uses a Hindley-Milner Type System (you can also say Hindley-Milner inference). The idea is to iteratively refine all the types of all the expressions until you find the best type for each. Get more information at some of these sources:
Further Study
Just for full disclosure, there’s a massive amount of Haskell not covered here. But hopefully enough was covered to be useful. You should continue your study beyond this introduction.
Some good reads and watches:
- The online book Learn You a Haskell for Great Good!
- The online Haskell book at Wikibooks
- The official Haskell 2010 Language Report
- The defacto home page of the Haskell language
- The Computerphile video To Infinity and Beyond
- The Haskell Reference Card
- The various courses on typeclasses.com by Julie Moronuki and Chris Martin
Feeling good about your Haskelling? Pour over the Blow your mind page on the Haskell wiki. That’s programming, right?