Logic

What is Logic?
Logic is the study of reasoning. It deals primarily with inference, but also entailment, causality, consequence, induction, deduction, truth, falsity, belief, fallacies, paradoxes, probabilities, analysis, tense, modality, necessity, sufficiency, possibility, identity, vagueness, existence, description, justification, tolerance, obligation, permission, relevance, assertion, validity, contradiction, provability, and argumentation.
One of the central questions explored in the study of logic is:
Does the conclusion follow from the premises?
The phrase “follow from” can have different interpretations, including, but not limited to:
We know a general rule to be valid. We see an instance of this rule, so we apply the general rule to show, with complete certainty, the truth of the specific instance.
We have seen a bunch of cases to be true, so we infer that a new related case is also true. We can’t be sure of our conclusion, though, since a few special cases cannot necessarily prove a general rule.
The premises give really strong evidence for the truth of the conclusion.
A Pretest
Have some fun! Take this logic pre-test.
Notation
In order to understand the form of arguments and not get bogged down in long, confusing, and often ambiguous text, we usually write statements in a very compact form. We often use common abbreviations such as the following. (As you read these descriptions, try not to let any preconceived notions of what you think is meant by “truth” color your interpretation.)
| Form | Meaning | Technical Term |
|---|---|---|
| $T$ | True | Truth |
| $F$ | False | Falsity |
| $\neg A$ | Not $A$ | Negation |
| $A \wedge B$ | $A$ and $B$ | Conjunction |
| $A \vee B$ | $A$ or $B$, or both | Disjunction |
| $A \supset B$ | It is not the case that $A$ is true and $B$ is false (i.e., whenever $A$ is true, $B$ is true) | Material Implication |
| $A \equiv B$ | $A$ and $B$ are either both true or both false | Material Equivalence |
| $A \rightarrow B$ | If $A$, then $B$ (non-truth-functional) | Conditional |
| $\forall x. A$ | For every $x$, $A$ | Universal quantification |
| $\exists x. A$ | There exists an $x$ such that $A$ | Existential quantification |
| $f\,x$ | The result of applying function $f$ to $x$ | Function application |
| $\iota x. A$ | The $x$ such that $A$ | Description |
| $x = y$ | $x$ and $y$ are the same object | Equality |
| $\Box A$ | In all possible worlds, $A$ | Necessity |
| $\lozenge A$ | In some possible world, $A$ | Possibility |
| $\mathbf{P} A$ | It was (at least once) the case that $A$ | Past |
| $\mathbf{F} A$ | It will (at least at some point) be the case that $A$ | Future |
| $\mathbf{H} A$ | It was always the case that $A$ | Always has been |
| $\mathbf{G} A$ | It will forever be the case that $A$ | Always going to be |
| $\mathscr{O} A$ | $A$ must (morally) be done | Obligation |
| $\mathscr{P} A$ | $A$ may (morally) be done | Permission |
| $\mathscr{K}_x A$ | Agent $x$ knows $A$ | Knowledge |
| $\mathscr{B}_x A$ | Agent $x$ believes $A$ | Belief |
| $|A|$ | Truth value of $A$ (in 0.0 ... 1.0) | Numerical Truth Value |
| $pr(A)$ | Probability of $A$ being true | Probability |
| $pr(A|B)$ | Probability of $A$ being true given that $B$ is true | Conditional Probability |
It takes quite a bit of practice to translate English (or other natural language) sentences into logical notation. In fact, the translation might not always be exact; natural language is pretty fluid (see, for example, The SEP article on Conditionals for the many readings of “if...then”). We’ll just give examples, rather than rules.
| English | Logic | Breakdown |
|---|---|---|
| Juliet is Italian | $\mathit{Italian(Juliet)}$ | — |
| $Ij$ | ||
| Romeo likes Juliet | $\mathit{Likes(Romeo,Juliet)}$ | |
| $Lrj$ | ||
| Romeo likes himself | $Lrr$ | Romeo likes Romeo |
| The sidewalk is wet when it rains | $R \supset Ws$ | If it is raining, then
the sidewalk is wet |
| Romeo likes the king’s daughter | $Lr(\iota x.Dkx)$ | Romeo likes
the person x such that
the daughter of the king is x |
| $Lr(dk)$ | Romeo likes the daughter of the king |
|
| Alice sees everybody | $\forall p. Sap$ | For every (person) p
Alice sees p |
| $\neg \exists p.\neg Sap$ | It is NOT the case that
there exists a (person) p such that
Alice does not see p |
|
| Alice sees somebody | $\exists p.Sap$ | There exists a (person) p such that
Alice sees p |
| $\neg \forall p. \neg Sap$ | It is NOT the case that
for every (person) p
Alice does not see p |
|
| Alice sees nobody | $\neg \exists p.Sap$ | It is NOT the case that
there exists a (person) p such that
Alice sees p |
| $\forall p. \neg Sap$ | For every (person) p
it is NOT the case that
Alice sees p |
|
| All apples are fruits | $\forall x.(Ax \supset Fx)$ | For every x
if x is an apple
x is a fruit |
| Some apples are green | $\exists x.(Ax \wedge Gx)$ | There exists an x such that
x is an apple AND x is green |
| All snakes are animals | $\forall x.(Sx \supset Ax)$ | For every thing x
if x is a snake
x is an animal |
| $\neg \exists x.(Sx \wedge \neg Ax)$ | It is NOT the case that
there exists an x such that
x is a snake AND x is not an animal |
|
| Some snakes are poisonous | $\exists x.(Sx \wedge Px)$ | There exists an x such that
x is a snake AND x is poisonous |
| $\neg \forall x.(Sx \supset \neg Px)$ | It is NOT the case that
for every x
if x is a snake
then x is non-poisonous |
|
| Juliet doesn’t like French people | $ \neg\exists p.(Fp \wedge Ljp)$ | It is NOT the case that
there exists a (person) p such that
p is French AND Juliet likes p |
| $\forall p.(Fp \supset \neg Ljp)$ | For every (person) p
if p is French
It is NOT the case that
Juliet likes p |
|
| Juliet likes all Italians | $\forall p.(Ip \supset Ljp)$ | For every (person) p
if p is Italian
Juliet likes p |
| Juliet likes all Italians except Romeo | $\forall p.(Ip \supset (Ljp \equiv \neg (p=r)))$ | For every (person) p
if p is Italian
Juliet likes p IF AND ONLY IF p is not Romeo |
| Every Italian likes someone | $\forall p. (Ip \supset \exists q.Lpq)$ | For every (person) p
if p is Italian
there exists (a person) q such that
p likes q |
| Everyone likes an Italian | $\forall p. \exists q.(Iq \wedge Lpq)$ | For every (person) p
there exists some q such that
q is Italian AND p likes q |
| Everyone likes this one particular Italian | $\exists q.(Iq \wedge \forall p.Lpq)$ | There exists a particular q such that
q is Italian
AND
for every (person) p
p likes this one particular q |
| Pablo shaves all and only those who do not shave themselves | $\forall q.(Spq \equiv \neg Sqq)$ | For every (person) q
Pablo shaves q
IF AND ONLY IF
it is not that case that
q shaves q |
| Not everyone is libertarian or progressive | $\neg \forall p.(Lp \vee Pp)$ | It is NOT the case that
there exists a (person) p such that
p is Libertarian OR p is progressive |
| $\exists p.(\neg Lp \wedge \neg Pp)$ | There exists a (person) p such that
p is NOT libertarian
AND
p is NOT progressive |
|
| Either the queen is rich or some pigs fly | $Rq \vee \exists p.(Pp \wedge Fp)$ | The queen is rich
OR
there exists a p such that
p is a pig AND p flies |
| Everything has a cause | $\forall x. \exists y.Cyx$ | For every (thing) x
there exists some y such that
y caused x |
| Everything has the same cause | $\exists y. \forall x.Cyx$ | There exists this one (uber thing) y such that
for every thing x
y caused x |
| Nothing caused itself | $\forall x. \neg Cxx$ | For every (thing) x
it is NOT the case that
x caused x |
| $\neg \exists x. Cxx$ | It is NOT the case that
there exists an x such that
x caused x |
|
| Everybody loves somebody, but someone is unloved | $(\forall x. \exists y.Lxy) \wedge (\exists x.\neg \exists y.Lyx)$ | For every (person) x
there is some (person) y such that
x loves y
AND ALSO
there exists some (person) x such that
it is NOT the case that
there exists some (person) y such that
y loves x |
| Some number less than 5 is a perfect square | $\exists x. (Lx5 \wedge \exists y.(x=qy))$ | There exists an x such that
x < 5
AND
the exists a y such that
x is y squared |
| $\exists x. (x<5 \wedge \exists y.(x=y^2))$ | ||
| Juliet might like Romeo | $\lozenge Ljr$ | It is possible that
Juliet likes Romeo |
| Two is necessarily equal to two | $\Box (2=2)$ | It is necessary that
2 equals 2 |
| The thunder god was worshiped by some Athenians | $\exists p.(Ap \wedge Wp(gt))$ | There exists a (person) p such that
p is an Athenian
AND
p worships
the god of thunder |
| It is possible that some day the sun-god will become forever awesome | $\lozenge \mathbf{FG}A(gs)$ | It is possible that
at some point in the future
it will always be the case that
that the god of the sun
is awesome |
| Juliet believes that Romeo doesn’t believe that Juliet likes him | $\mathscr{B}_j(\neg \mathscr{B}_r Ljr)$ | Juliet believes that
it is not the case that Romeo believes that
Juliet likes Romeo |
| There is a better than 50-50 chance that Juliet is hungry when it’s raining | $pr(Hj \mid R) > 0.5$ | The probability that
Juliet is hungry,
given that it’s raining
is bigger than 0.5 |
Besides the logical operators ($\neg$, $\wedge$, $\vee$, $\supset$, $\equiv$, $\forall$, $\exists$, $\iota$, $=$, $\Box$, $\lozenge$, $\textbf{P}$, $\mathscr{B}$, $pr$, and so on), there are two kinds of things we talk about:
- Terms: These represent objects (a.k.a. individuals), like $r$ for Romeo, $j$ for Juliet, $k$ for the king, $2$ for the number two. Terms can be made by applying functions to other terms. For example, if $d$ is the function “daughter of” then $dk$ denotes the daughter of the king, and if $t$ was the country Türkiye and $c$ was the function “capital of” then $ct$ is the capital of Türkiye. If $p$ were the plus function, then $pxy$ represents $x + y$.
- Formulas: These are things that are assigned truth values. Examples are $T$ for truth, $F$ for falsity, $R$ for “it’s raining.” Formulas can be made by applying predicates. We saw examples in the table above of $Lrj$ (Romeo likes Juliet) and $Ws$ (the sidewalk is wet).
Note that we use lowercase letters in the term world and uppercase letters in the formula world, even when using variables that stand for terms vs. formulas.
Be careful not to confuse terms and formulas. For example, note $\iota x. Px$ is a term, but $\exists x. Px$ is a formula.
ParenthesesBe sure to use parentheses when needed. For example, $Pfb$ is an application of the two-argument predicate $P$ to $f$ and $b$, for instance “Farah pressed the button”; but in $P(fb)$, $P$ is a one-argument predicate and $f$ is a function, as in “The friend of Billie is popular.”
When it comes to binary operators, $\neg$ has the highest precedence, then $\wedge$, then $\vee$ then $\supset$ then $\equiv$. The . has the lowest! So $\exists x. Px \wedge Q$ means $\exists x. (Px \wedge Q)$ and does NOT mean $(\exists x. Px) \wedge Q$. Parentheses are required in the latter.
A logical argument is written as a sequence of formulas. We check the validity of the argument by checking whether each formula is either (1) a premise or (2) follows from previous formulas. Arguments can also be given graphically, with premises above the line and conclusions below. Example:
| $B$ | |
| $A \vee B$ | $\neg B$ |
| $A$ | |
The meaning of “follows from” depends on the particular system of logic you are working under.
So let’s look at different kinds of logic.
Kinds of Logic
How can there be many different kinds of logic? Well, for one there could be different ways to understand “truth.” Sometimes we aren’t concerned with exact truth, but rather “degree of belief,” or whether something is “justified,” or “achievable,” or “knowable.”
Here are some kinds of logics. The list is incomplete. The kinds are also overlapping.
Bivalent Logic
A bivalent system has exactly two truth values, usually called true and false. What kinds of systems are not bivalent? Those with a third value (sometimes called “unknown”), and those where a truth value is represented as a degree of certainty or belief (e.g. a value ∈ 0.0..1.0).
Propositional Logic
Technically, a proposition is a predicate with no arguments, such as “It‘s raining”. (We saw this in the example above, where we represented this with $R$.)
Sometimes though, we can put ourselves in a world in which information is just rolled up into single, atomic, nondecomposable sentences. Then propositions can be things like “Pigs fly”, “I am late”, “The moon is square”, and “The baby wants to sleep”. Propositional Logic is a system of reasoning about these things without decomposing them. The traditional operators are:
| Form | Meaning |
|---|---|
| $P \wedge Q$ | $P$ and $Q$ |
| $P \vee Q$ | $P$ or $Q$ (or both) |
| $\neg P$ | not $P$ |
| $P \supset Q$ | $P$ materially implies $Q$; e.g., $\neg(P \wedge \neg Q)$, or equivalently, $\neg P \vee Q$ |
| $P \equiv Q$ | $P$ and $Q$ have the same truth value |
| $P \wedge Q$ | means “Pigs fly and the queen is rich” |
| $\neg Q \vee P$ | means “The queen is not rich or pigs fly” |
| $(P \vee Q) \wedge (\neg P \wedge \neg Q)$ | means “Pigs fly or the queen is rich, but not both” |
Note: The $\wedge$ and $\vee$ operators are meant to be material, not causal. They cannot distinguish the sentence “I called her and found out about the problem” from “I found out about the problem and called her.”
Syllogistic Logic
Systems of logic featuring syllogisms were studied thousands of years ago; they include reasoning about “all” and “some”, but do not allow general propositions nor connectives like “and” and “or”. Traditionally, only the following eight kinds of statements are considered (capital letters are classes, small letters are instances):
| Form | Example |
|---|---|
| $x$ is $A$ | Socrates is human |
| $x$ is not $A$ | Fido is not human |
| $x$ is $y$ | Obama is the 44th U.S. President |
| $x$ is not $y$ | Italy is not the 2016 Olympic champion in Women’s Water Polo |
| All $A$ are $B$ | All dogs are mammals |
| No $A$ is $B$ | No dogs are fish |
| Some $A$ are $B$ | Some birds are flyers |
| Some $A$ are not $B$ | Some markers are not green |
For historical use onlySyllogistic logic has been completely superseded by first-order predicate logic.
Predicate Logic
A predicate logic adds objects, functions on objects, predicates, descriptions, and quantifiers (such as $\exists$ and $\forall$) to propositional logic. A first-order logic allows quantification over objects only; In a second-order logic you can quantify over first-order predicates. You can go on forever with these orders.
For each of the eight examples of syllogistic forms above, we will write the corresponding formula in first-order logic.
Here is an example of a second-order logic formula. Do you recognize it? It’s the “principle of mathematical induction,” where $s$ is the successor function (that is, $sn = n+1$):
$\forall P.((P0 \wedge \forall n.(Pn \supset P(sn))) \supset \forall n.Pn)$
Classical Logic
Classical Logic is probably the most widely used logic. It is characterized by six properties (so say one of the authors of the Wikipedia article on the subject):
- Bivalency
- Excluded middle: $A \vee \neg A$
- Non-contradiction: $\neg (A \wedge \neg A)$
- Monotonicity of entailment: If $B$ follows from $A$, then it follows from $A$ and $C$ (in other words, go ahead and add assumptions!)
- Commutativity of conjunction: $A \wedge B$ has the same truth value as $B \wedge A$
- DeMorgan dualities for all operators: $\neg P(A_1,...,A_n)$ has the same truth value as $Q(\neg A_1,...,\neg A_n)$, where $P$ and $Q$ are duals of each other. (Examples: $\wedge$ and $\vee$ are duals; $\forall$ and $\exists$ are duals. There are many others.)
The term “classical” here does mean old or ancient. This was not the logic of the Ancient Greeks, the Ancient Chinese, or the Ancient anyone else. Classical Logic dates from the late 1800s. It’s relatively new.
Intuitionistic Logic
In intuitionistic logic (often identified with constructive logic), we are not concerned with the truth of a statement as much as we are about its justification. Every theorem is something justifiable, constructively. So $A$ means “$A$ is provable” and $\neg A$ means “$A$ is refutable” (i.e., it is provable that no proof of $A$ exists—in other words, assuming A allows you to derive False). Therefore:
- You can only prove $A \vee \neg A$ by proving $A$ or refuting $A$. (The inability to do neither means you can’t say anything, so shut up.)
- You can only prove $\exists x. P$ by demonstrating an object for which $P$ is true. You cannot prove it by saying “it just can’t be the case that $\neg P$ holds for every $x$.”
- You can derive $\neg \neg A$ from $A$, but you cannot derive $A$ from $\neg \neg A$. The former says “if I can prove $A$, then I can refute that $A$ is refutable” but the latter is saying “if there’s no proof that $A$ is not provable then $A$ must be provable.” That’s not good enough: you have to demonstrate the proof of $A$ in order for $A$ to be a theorem!
You read things a bit differently:
- $A \wedge B$ means “I can construct a proof of $A$ and a proof of $B$”
- $A \vee B$ means “I can construct a proof of $A$ or a proof of $B$”
- $A \supset B$ means “From a proof of $A$, I can construct a proof of $B$”
- $\forall x. P$ means “for every $x$, I can construct a proof of $P$”
- $\exists x. P$ means “I can find an $x$ for which I can construct a proof of $P$”
The big thing is that intuitionistic logic rejects the excluded middle as an “axiom.”
Constructive logic codifies the principles of mathematical reasoning as it is actually practiced. In mathematics a proposition may be judged to be true exactly when it has a proof, and may be judged to be false exactly when it has a refutation. Because there are, and always will be, unsolved problems, we cannot expect in general that a proposition is either true or false, for in most cases we have neither a proof nor a refutation of it. Constructive logic may be described as logic as if people matter, as distinct from classical logic, which may be described as the logic of the mind of god. From a constructive viewpoint the judgment “φ true” means that “there is a proof of φ.” —Robert Harper, Practical Foundations of Programming Languages, Chapter 30.
Intuitionistic logic turns out to be ideal for computer science.
Learn more at Wikipedia and the SEP.
Relevance Logic
Classical logic has the principle of explosion: false implies everything. Or in other words, “from a contradiction, everything follows.” The rationale is: if things are only true or false, and you assume false is true, then everything is true because true is already true and now you say that false is true also.
Let’s demonstrate with a proof of $(A \wedge \neg A) \supset B$:
| 1. $A$ | Assumption |
| 2. $\neg A$ | Assumption |
| 3. $A \vee B$ | By monotonicity of entailment (1) |
| 4. $B$ | Assumption (2) cancels the left part of (3) |
This means the following statements are true in classical logic:
- If the moon is six inches in diameter, then 2 + 2 = 4.
- If the moon is six inches in diameter, then 2 + 2 = 5.
- If the moon is six inches in diameter, then the moon is seven inches in diameter.
Relevance logic rejects explosion, and requires the antecedent and consequent to be related to each other. There must be some real causality. We say in classical logic, implication is material but in relevance logic it is strict. There are many different ways to encode relevance.
Read about Relevance Logic in the SEP.
Free Logic
Descriptions can be tricky. What if no object satisfies the description?
Russell regarded $P(\iota x.Ax)$ as an abbreviation for $\exists x.((\forall y.(Ay \equiv y=x)) \wedge Px)$. But this means the statement is false unless there is a unique object satisfying the description $A$ and that has the property $P$.
A free logic allows the description of terms that do not denote anything. Read about Free Logic in the SEP.
Non-monotonic Logic
A non-monotonic logic rejects the monotonicity of entailment. If a logic is monotonic, then adding new information can change the set of known facts, causing previously known truths to become falsehoods. These kind of logics are good for cases where you have to retract previous knowledge when new facts are known, as in
- default reasoning
- abductive reasoning (infer the most likely cause)
- reasoning about knowledge (I used to not know this, now I do)
- belief revision
See the SEP article on non-monotonic logic.
Paraconsistent Logic
A paraconsistent logic is one that allows contradictions.
See the SEP article on Paraconsistent Logic.
Many-Valued Logics
A many-valued logic has, you got it, many truth-values. Many such systems exist. What’s useful about them is they get rid of the those principles of excluded middle and non-contradiction.
You might be interested in four-valued logics.
Catuṣkoṭi
The Catuṣkoṭi is also known as the “Four Corners.” Propositions take on four values :
- Being
- Not Being
- Being and Not Being
- Neither Being nor Not Being
Find out more at Wikipedia and the SEP and this lecture by Graham Priest.
Fuzzy Logic
A fuzzy logic is one in which facts have a degree of truth between 0 and 1. It is useful for statements like “$X$ is tall” or “$X$ is an adult” or “The bike is new.”
Do not confuse fuzzy logic with paraconsistent logic.
Do not confuse fuzzy logic with probability theory.
Read about Fuzzy Logic in the SEP.
Modal Logic
Modal Logic deals with modalities, which qualify statements somehow. There are many different kinds of modalities, giving rise to different kinds of logics. Each can be based on classical or non-classical logics, and use numeric truth values, too.
See the SEP article on modal logic.
Alethic Logic (Necessity and Possibility)
The basic alethic modal operators are defined as:
| Form | Meaning |
|---|---|
| $\Box A$ | It is necessary that A |
| $\lozenge A$ | It is possible that A |
In classical modal logic, the two operators are duals:
- $\Box A \equiv \neg \lozenge \neg A$
- $\lozenge A \equiv \neg \Box \neg A$
- $\neg \Box A \equiv \lozenge \neg A$
- $\neg \lozenge A \equiv \Box \neg A$
Deontic Logic (Obligation and Permission)
The basic deontic operators are defined as:
| Form | Meaning |
|---|---|
| $\mathscr{O}A$ | It is obligatory that $A$, or $A$ ought to be (MUST) |
| $\mathscr{P}A$ | It is permissible that $A$, or $A$ is allowed (MAY) |
Epistemic Logic (Knowledge)
In epistemic logic we have:
| Form | Meaning |
|---|---|
| $\mathscr{K}_x A$ | Agent x knows A |
| $\mathscr{K} A$ | A is known (by all agents or by some agent whose identity we assume from context) |
Doxastic Logic (Belief)
In doxastic logic we have:
| Form | Meaning |
|---|---|
| $\mathscr{B}_x A$ | Agent x believes A |
| $\mathscr{B} A$ | A is believed (by all agents or by some agent whose identity we assume from context) |
You may sometimes see the epistemic and the doxastic distinguished in the following context. Let $\Gamma = \exists g. G g$, i.e., there exists a $g$ such that $g$ is a god, or “(at least one) god exists.” Then:
- $\mathscr{K}_x\,\Gamma \wedge \mathscr{B}_x\,\Gamma$ means $x$ is a gnostic theist
- $\mathscr{K}_x\,\Gamma \wedge \neg \mathscr{B}_x\,\Gamma$ means $x$ is a gnostic atheist
- $\neg \mathscr{K}_x\,\Gamma \wedge \mathscr{B}_x\,\Gamma$ means $x$ is an agnostic theist
- $\neg \mathscr{K}_x\,\Gamma \wedge \neg \mathscr{B}_x\,\Gamma$ means $x$ is a agnostic atheist
Temporal Logic
Temporal logic deals with the modalities of time.
| Form | Meaning |
|---|---|
| $\mathbf{P}A$ | $A$ was true (at some point) in the Past |
| $\mathbf{F}A$ | $A$ will be true (at some point) in the Future |
| $\mathbf{H}A$ | $A$ Has always been true |
| $\mathbf{G}A$ | $A$ is always Going to be true |
Dynamic Logic
Dynamic Logic brings events into the picture:
| Form | Meaning |
|---|---|
| $[e]A$ | “After event $e$, $A$ is necessarily true” |
| $\langle e \rangle A$ | “After event e, A is possibly true” |
Temporal vs. Dynamic Logic
Temporal logic [is] the modal logic of choice for reasoning about concurrent systems with its aspects of synchronization, interference, independence, deadlock, livelock, fairness, etc. These concerns of concurrency would appear to be less central to linguistics, philosophy, and artificial intelligence, the areas in which dynamic logic is most often encountered nowadays. — Wikipedia
Formal Logic
In logic we are not so much concerned with the absolute truth or falsity of individual premises themselves, but rather with the form of arguments. We can deal with “forms” using a formal systems. Formal systems manipulate formulas.
A formal system is a mechanism for symbolically generating a set of formulas (called theorems) via inference rules.
A logistic system (a.k.a. a system of formal logic) is a formal system in which formulas are assigned truth values.
To define a logistic system we need three parts:
Syntax
What the possible formulas are
Semantics
What the formulas mean
Inference Rules
How formulas can be derived from other formulas
The inference rules capture the reasoning process.
We need examples.
Syntax
A syntax gives a rigorous, formal specification of exactly what is and what is not a formula.
Example. Here is the syntax of classical propositional logic:
- A variable is $p$, $q$, $r$, or a variable followed by a prime ($'$) symbol. Nothing else is a variable.
- A formula is $T$, $F$, any variable, or, for any formulas $A$ and $B$, $\neg A$, $(A \wedge B)$, $(A \vee B)$, $(A \supset B)$, or $(A \equiv B)$. Nothing else is a formula.
This means that, for example:
p
(¬(p′′′ ∧ q) ∨ ¬¬p)
(r ⊃ p′)
are formulas, but
¬≡pp∧))′∧¬q∨(F′′
is not. Neither, by the way is p ∧ q, since the syntax above requires parentheses around all formulae formed with binary operators. Look again, closely!
Wait, what? Parentheses are...required?In this formal syntax, yes they are. That said, you are free to write another formal syntax to capture operator precedence if you like, or you can allow for an informal representation of formulas in which precedence is assumed.
Semantics
A semantics assigns truth values to each formula. Because variables are permitted, any semantics would have to take into account the truth values of variables before computing the truth values of formulas. That is, while we may be able to assign a truth value of false to $p \wedge \neg p$, the truth value of $p \supset q$ depends on the previously assigned values of $p$ and $q$. We call a mapping of variables to truth values an interpretation and require semantic definitions to be relative to an interpretation. Here is a semantic definition for classical propositional logic:
For classical propositional logic, we can define the semantics as follows:
- The meaning of $T$ relative to any interpretation is true.
- The meaning of $F$ relative to any interpretation is false.
- The meaning of $p$ relative to interpretation $\phi$ is $\phi(p)$.
- The meaning of $(A \wedge B)$ relative to $\phi$ is true if both of the meanings of $A$ relative to $\phi$ and $B$ relative to $\phi$ are true; and false otherwise.
- The meaning of $(A \vee B)$ relative to $\phi$ is true if either or both of the meanings of $A$ relative to $\phi$ and $B$ relative to $\phi$ are true; and false otherwise.
- The meaning of $(A \supset B)$ relative to $\phi$ is true if the meaning of $A$ relative to $\phi$ is false or the meaning of $B$ relative to $\phi$ is true, or both; and false otherwise.
- The meaning of $(A \equiv B)$ relative to $\phi$ is true if the meanings of $A$ relative to $\phi$ and $B$ relative to $\phi$ are both true or both false; and false otherwise.
Don’t mix syntax and semanticsIn particular, note that $T$ is a syntactic element, a formula, just a symbol; while true is from the world of semantics.
$(\neg p \wedge (r \supset \neg q)) \vee p)$
under an interpretation in which $p$ is mapped to true, $q$ to false, and $r$ to true.We’re interested ultimately in valid reasoning—what follows from what—so let’s define some terms:
- Satisfiability
- If formula $A$ is true under some interpretation $\varphi$ we write $\vDash_{\varphi}A$ and say $\varphi$ satisfies $A$, or that $A$ is satisfiable.
- Validity
- If formula $A$ is true under all interpretations we write $\vDash A$ and say A is a tautology, or that $A$ is valid.
- Entailment
- If formula $A$ is true under all interpretations in which formula $B$ is true, we write $B \vDash A$ and say $B$ entails $A$. Entailment is central to reasoning; if our knowledge base contains $B$ and we know that $B$ entails $A$, we know, then, that $A$ is true.
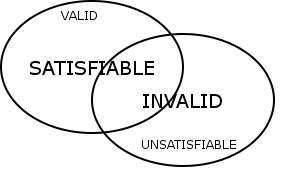
- If a formula is valid, then it is satisfiable
- If a formula is unsatisfiable, then it is invalid
- In classical propositional logic, $A$ is valid iff $\neg A$ is unsatisfiable
- In classical propositional logic, $A$ is invalid iff $\neg A$ is satisfiable
- In classical propositional logic, satisfiability and validity are duals
Inference Rules
In a logistic system, we don’t necessarily compute semantic functions for the fun of it. Instead, we apply inference rules to algorithmically, (or mechanistically, typographically, symbolically) generate a formulas in such a way as to mimic a reasoning process. Define
$\{A_1, ..., A_n\} \vdash B$
to mean “$B$ given assumptions $A_1, ..., A_n$.” The inference rules of a logistic system produce these kinds of statements.
Example: The inference rules of classical propositional logic are these:
If $\varnothing \vdash A$, we say $A$ is a theorem and write $\vdash A$. The sequence of inferences producing a theorem is a proof of that theorem.
| 1. $(p \wedge (p \supset q)) \vdash (p \wedge (p \supset q))$ | ASSUME |
| 2. $(p \wedge (p \supset q)) \vdash p$ | CONJ-ELIM (1) |
| 3. $(p \wedge (p \supset q)) \vdash (p \supset q)$ | CONJ-ELIM (1) |
| 4. $(p \wedge (p \supset q)) \vdash q$ | IMP-ELIM (2, 3) |
| 5. $(p \wedge (p \supset q)) \vdash (p \wedge q)$ | CONJ-INTRO (2, 4) |
| 6. $\vdash ((p \wedge (p \supset q)) \supset (p \wedge q))$ | IMPL-INTRO (5) |
- $\neg F$
- $(p \supset (q \supset p))$
- $(p \vee \neg p)$
- $((p \supset q) \equiv (\neg p \vee q))$
- $((p \equiv q) \supset ((p \wedge q) \vee (\neg p \wedge \neg q)))$
- $((p \wedge \neg p) \supset q)$
- $((p \vee (q \wedge r)) \supset (p \vee q))$
Other Logistic Systems
For first-order predicate logic, we have this syntax (all categories are defined inductively):
- A constant is $a$, $b$, $c$, etc. or a constant followed by a $'$. A function symbol is $f$, $g$, $h$, etc. or a function symbol followed by a $'$.
- A variable is $x$, $y$, $z$, or a variable followed by a prime ($'$) symbol.
- A term is a variable, a constant, or $f(t_1, \ldots t_n)$ for function symbol $f$ and terms $t_i$.
- A formula is $T$, $F$, or, for any variable $v$ and formulas $A$ and $B$, $\neg A$, $(A \wedge B)$, $(A \vee B)$, $(A \supset B)$, $(A \equiv B)$, $(\exists v.A)$, and $(\forall v.A)$.
Parentheses can be removed as long as precedence is respected.
The semantics and the inference rules are much more complicated to define for first-order logic than for propositional (0th-order logic). We need:
- A structure that includes a domain of objects and interpretations for function symbols and predicates.
- The concept of a free variable. A variable $x$ is free in a formula $A$ if it is not bound by (in the scope of) a quantifier. Example: in the formula $\exists x. Pxy$, we have that $x$ is bound and $y$ is free.
- The concept of a substitution. The notation $A[t/x]$ refers to the term made from $A$ by substituting $t$ for all free occurrences of $x$ such that no variables in get captured after the substitution.
We'll leave the details of the syntax and inference rules for first-order logic to Wikipedia. For the history of how first-order logic came to be the workhorse of mathematics and semantics, see this really cool SEP article.
For alethic modal logic, which add the operators $\Box$ and $\lozenge$ to predicate logic, there are quite a few versions, based on the axioms and inference rules they add to the underlying logic. Here are some examples:
- System K, the weakest form of modal logic, adds the following to an underlying logic:
- From $\Box(A \supset B)$ infer $\Box A \supset \Box B$
- If $A$ is a theorem of the underlying logic, infer $\Box A$
- System T is System K plus
- From $\Box A$ infer $A$
- S4 is System T plus
- From $\Box A$ infer $\Box \Box A$
- S5 is System T plus
- From $\lozenge A$ infer $\Box \lozenge A$
Properties of Logistic Systems
The definition of truth in a system is generally just stated in precise natural language, or with semantic functions (as in our example above). The derivation of theorems, however, is a purely mechanical process. We would like to know how well, in a logistic system, theorem derivation (proof) correlates with truth.
- Soundness
- A system is sound iff every theorem is true, e.g., if $\vdash A$ then $\vDash A$.
- Completeness
- A system is complete iff every true formula is a theorem, e.g., if $\vDash A$ then $\vdash A$.
- Consistency
- A system is consistent iff no two theorems have contradictory truth values (where “contradictory” depends on the type of logic being considered).
- Decidability
- A system is decidable iff there exists an (always-terminating) algorithm to determine whether or not a given formula is a theorem.
The reasoning about logistic systems themselves is called metalogic.
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- Logic is the study of ________________. reasoning
- What is the difference between deduction and induction? In particular how are they in some sense opposites of each other? Deduction goes from the general to the specific (and hence always gives a valid conclusion when the premises are true); induction goes from the specific to the general (and is therefore not guaranteed to give you a valid conclusion).
- What is abduction? Drawing conclusions from strong evidence.
- What is the difference between $=$ and $\equiv$? $x = y$ means that $x$ and $y$ refer to the same object, while $A \equiv B$ means that the two formulas $A$ and $B$ have the same truth value.
- What is an equivalent formula of $A \supset B$, in terms of $\vee$? $\neg A \vee B$
- What is an equivalent formula of $A \supset B$, in terms of $\wedge$? $\neg (A \wedge \neg B)$
- What is the difference between $A \supset B$ and $A \rightarrow B$? The former has no notion of causality; it just simply says there is no way $A$ can be true while $B$ is false. It does not say that the truth of $A$ causes $B$. The latter says that.
- Describe two ways to represent the object “The president of Mexico” in common logic notation, one with the description operator and the other with a function. $\iota p. P m p$, where $m$ is Mexico and $Pxy$ means “the president of $x$ is $y$.”
$pm$ where $p$ is the function “president of” and $m$ is Mexico. - How do you represent the formula “Juliet once believed that Romeo might someday forever live in Canada”? $\mathbf{P}(\mathscr{B}_j\lozenge\mathbf{F}\mathbf{G}(Lrc))$, where $j$ is Juliet, $r$ is Romeo, $c$ is Canada, and $Lxy$ means $x$ lives in $y$.
- Give the formula $A \vee B \wedge C \equiv D \supset E$ in its fully-parenthesized form. $((A \vee (B \wedge C)) \equiv (D \supset E))$
- Give the formula $A \wedge \forall x. Px \supset \neg Qxy$ in its fully-parenthesized form. $(A \wedge (\forall x. (Px \supset \neg Qxy)))$
- How to we diagram the inference that $C$ follows from $A$ and $B$? $\dfrac{A \;\;\;\; B}{C}$
- What is a bivalent logic? A logic in which every formula has one of two truth values (generally $T$ or $F$).
- What is a proposition? A predicate of zero arguments. As such, it can be considered a formula on its own, and importantly, it is atomic (nondecomposable).
- What is prepositional logic good for, if anything? It is too weak to be useful for much really, but its simplicity (1) makes it a good introductory logic for learners, and (2) is an example of a system that is both sound and complete.
- What are the study of syllogisms relegate to these days? The history of logic, since first-order predicate logic encompasses all syllogistic forms and much more.
- The principle of mathematical induction is an formula of ________________-order predicate logic. Second
- What characterizes classical logic? Try to list all six features. (1) Bivalence, (2) excluded middle, (3) non-contradiction, (4) monotonicity of entailment, (5) commutativity of conjunction, (6) dualities of conjunction/disjunction and of universal/existential quantification.
- What is intuitionistic logic most concerned with? Proof, rather than truth.
- What is a free logic and why might a computer scientist care? A free logic is one that does not require that all terms refer to objects. Computer scientists may find ways to deal with that horrible
nullthing. - Why is paraconsistent logic interesting? Humans seem to get by just fine with contradictions.
- What are the four corners of the Catuṣkoṭi? Being, Not Being, Being and Not Being, Neither Being nor Not Being.
- How is fuzzy logic different from probability theory? Fuzzy logic deals with degrees of truth, while probability theory deals with likelihoods.
- What is an alethic logic concerned with and what are its basic operators? Alethic logic is concerned with necessity and possibility. Its basic operators are $\Box$ and $\lozenge$.
- What is a deontic logic concerned with and what are its basic operators? Deontic logic is concerned with obligation and permission. Its basic operators are $\mathscr{O}$ and $\mathscr{P}$.
- What is an epistemic logic concerned with and what are its basic operators? Epistemic logic is concerned with knowledge. Its basic operators are $\mathscr{K}$ and $\mathscr{K}_x$.
- What is a doxastic logic concerned with and what are its basic operators? Doxastic logic is concerned with belief. Its basic operators are $\mathscr{B}$ and $\mathscr{B}_x$.
- In dynamic logic, how do we denote that after event $e$ occurs, $A$ must be true? How do we denote that after $e$ occurs, $A$ might be true? We write $[e]A$ and $\langle e \rangle A$ respectively.
- What are the three parts of a definition of a formal logistic system? Syntax, semantics, inference rules.
- What is an interpretation in formal logic, and why are they needed? An interpretation is a mapping of variables to truth values. They are needed because the truth value of a formula depends on the truth values of its variables.
- What does the notation $\mathcal{H} \vdash A$ mean? That $A$ should hold under the assumptions in $\mathcal{H}$.
- What do we call a formula $A$ for which $\vdash A$ holds? A theorem.
- What do we call a formula $A$ for which $\vDash A$ holds? A tautology (or a valid formula.)
- How are validity and satisfiability related? If something is valid then it is satisfiable, but not the other way around. (Similarly, if something is unsatisfiable, then it is invalid, but not the other way around.)
- Give an example of a valid statement of (classical) prepositional logic. $p \vee \neg p$
- Give an example of a invalid statement of (classical) prepositional logic. $p \wedge \neg p$
- Give an example of a satisfiable statement of (classical) prepositional logic that is neither valid nor invalid. $p \supset \neg p$
- What is a theorem in formal logic? A formula that is an axiom or that is derived from axioms via inference rules.
- What does it mean for a logistic system to be sound? Every theorem is true.
- What does it mean for a logistic system to be complete? Every true formula is a theorem.
- What does it mean for a logistic system to be consistent? No two theorems have contradictory truth values.
- What does it mean for a logistic system to be decidable? There exists an algorithm (always-terminating effective procedure) to determine whether a given formula is a theorem.
- What do we call the field that studies properties of logistic systems, such as soundness, completeness, consistency, and decidability? Metalogic.
Summary
We’ve covered:
- What logic is concerned with
- Common logic symbols
- Many kinds of logics
- Formal Logic
- Axioms, Theorems, and Inference Rules
- Metalogic (soundness, consistency, completeness, decidability)