1. $L_1 \cup L_2 = \{ 0, 011, 10, 1\}$
2. $L_1 \cap L_2 = \{ 10 \}$
3. $L_1L_2 = \{ 010, 01, 01110, 0111, 1010, 101 \}$
4. ${L_2}^* = \{ \varepsilon, 10, 1, 1010, 101, 110, 11, 101010, 10101, \ldots \}$

1. The empty language

   $\begin{array}{l} \textrm{There are NO rules in this grammar} \\ \end{array}$

   The empty language, the language of no strings, is absolutely NOT the same as the language containing only the empty string.

   While the best answer is that the grammar has a empty set of rules, it is also acceptable to create a one-rule grammar of the form $s \longrightarrow s$. In this grammar, you can never derive anything, so, it does work, but it’s not a great answer.

2. $\{ 0^i1^j2^k \mid i=j \vee j=k \}$

   $\begin{array}{lcl} \textit{s} & \longrightarrow & \textit{x}\;\texttt{"2"}^* \mid \texttt{"0"}^* \;\textit{y} \\ \textit{x} & \longrightarrow & \varepsilon \mid \texttt{"0"}\;\textit{x}\;\texttt{"1"} \\ \textit{y} & \longrightarrow & \varepsilon \mid \texttt{"1"}\;\textit{y}\;\texttt{"2"} \\ \end{array}$

3. $\{ w \in \{0,1\}^* \mid w \textrm{ does not contain the substring 000} \}$

   $\begin{array}{lcl} s & \longrightarrow & (\textit{x}\;\texttt{"1"})^*\;\textit{x} \\ x & \longrightarrow & ε \mid \texttt{"0"} \mid \texttt{"00"} \end{array}$

   This generates an arbitrary number of “chunks” of at most two zeros separated by 1s

4. $\{ w \in \{a,b\}^* \mid w \textrm{ has twice as many $a$'s as $b$'s} \}$

   $\begin{array}{lcl} s & \longrightarrow & x^* \\ x & \longrightarrow & \texttt{"a"}\;\textit{x}\;\texttt {"a"}\;\textit{x}\;\texttt{"b"} \mid \texttt{"a"}\;\textit{x}\;\texttt{"b"}\;\textit{x}\;\texttt {"a"} \mid \texttt{"b"}\;\textit{x}\;\texttt{"a"}\;\textit{x}\;\texttt{"a"} \\ \end{array}$

   This generates zero or more “chunks” each of which has twice as many $a$’s as $b$’s. There are three ways to form a chunk: (1) $\texttt{a---a---b}$, (2) $\texttt{a---b---a}$, and (3) $\texttt{b---a---a}$.

5. $\{ a^nb^na^nb^n \mid n \geq 0 \}$

   $\begin{array}{lcll} s & \longrightarrow & (\texttt{"a"}\;0\;\texttt{"b"}\;1\;\texttt{"a"}\;2\;\texttt{"b"})? & \textrm{Place marks between blocks} \\ \texttt{"a"}\;0 & \longrightarrow & \texttt{"aa"}\;0\;x & \textrm{New a's at the beginning} \\ x\;\texttt{"b"} & \longrightarrow & \texttt{"b"}\;x & \textrm{Move x's to the right of b's} \\ x\;1 & \longrightarrow & \texttt{"b"}\;1\;x & \textrm{When x hits the 1, make a new b} \\ x\;\texttt{"a"} & \longrightarrow & \texttt{"a"}\;x & \textrm{Move x past the second batch of a's} \\ x\;2 & \longrightarrow & \texttt{"a"}\;2\;\texttt{"b"} & \textrm{When x hits the 2, generate an ab on the right} \\ 0 & \longrightarrow & ε & \textrm{Drop the marks at any time} \\ 1 & \longrightarrow & ε & \\ 2 & \longrightarrow & ε & \\ \end{array}$

   There is probably a much better way.

To show the grammar in the standard $(V, \Sigma, R, S)$ form we have to get rid of all the wonderful convenient operators and introduce new variables. Here I added $s$ to stand for “sequence of one or more digits.” Also, since $e$ appears in the language but was also being used as a variable, I’ve changed the $e$ variable to $x$ (still stands for “exponent part”).

$\begin{array}{l} (\\ \;\;\;\; \{ n, s, f, x, d \}, \\ \;\;\;\; \{ 0,1,2,3,4,5,6,7,8,9,.,E,e,+,- \}, \\ \;\;\;\; \{ \\ \;\;\;\;\;\;\;\; (n, sfx), \\ \;\;\;\;\;\;\;\; (s, d), (s, ds), \\ \;\;\;\;\;\;\;\; (f,ε), (f,.s), \\ \;\;\;\;\;\;\;\; (x,ε), (x,Es), (xE+s), (x,E-s), (x,es), (x,e+s), (x,e-s), \\ \;\;\;\;\;\;\;\; (d,0), (d,1), (d,2), (d,3), (d,4), (d,5), (d,6), (d,7), (d,8), (d,9) \\ \;\;\;\; \}, \\ \;\;\;\; n \\ ) \\ \end{array}$

Turing Machine recognizers:

1. $\{w \in \{a,b\}* \mid w \textrm{ ends with } abb\}$

   

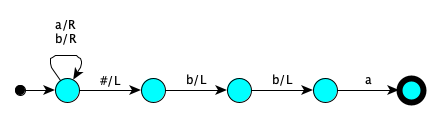
   State	Symbol	Actions	Next
   GoingToEnd	$a$	Right	GoingToEnd
   GoingToEnd	$b$	Right	GoingToEnd
   GoingToEnd	$\#$	Left	AtLast
   AtLast	$b$	Left	AtSecondToLast
   AtSecondToLast	$b$	Left	AtThirdToLast
   AtThirdToLast	$a$	—	Accept

2. $\{ w \in \{a,b\}^* \mid \#_a(w) = \#_b(w) \}$ (same number of $a$'s as $b$'s)

   

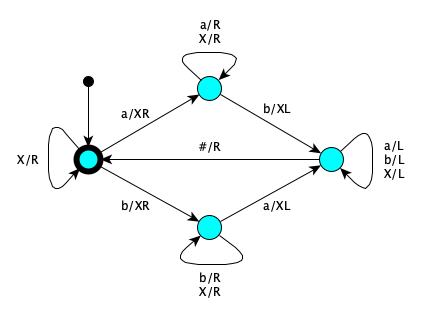
3. $\{w \in \{a,b\}* \mid w \textrm{ alternates } a\textrm{'s and } b\textrm{'s} \}$

   State	Symbol	Actions	Next
   Accept	$X$	Right	Accept
   Accept	$a$	Print $X$, Right	LookingForFirstB
   Accept	$b$	Print $X$, Right	LookingForFirstA
   LookingForFirstA	$X$	Right	LookingForFirstA
   LookingForFirstA	$b$	Right	LookingForFirstA
   LookingForFirstA	$a$	Print $X$, Left	ReturningToStart
   LookingForFirstB	$X$	Right	LookingForFirstB
   LookingForFirstB	$a$	Right	LookingForFirstB
   LookingForFirstB	$b$	Print $X$, Left	ReturningToStart
   ReturningToStart	$X$	Left	ReturningToStart
   ReturningToStart	$a$	Left	ReturningToStart
   ReturningToStart	$b$	Left	ReturningToStart
   ReturningToStart	$\#$	Right	Accept



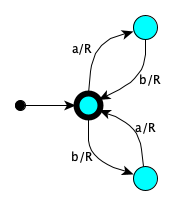
State	Symbol	Actions	Next
Accept	$a$	Right	NeedB
Accept	$b$	Right	NeedA
NeedA	$a$	Right	Accept
NeedB	$b$	Right	Accept

4. $\{ a^nb^na^nb^n \mid n \geq 0 \}$

   

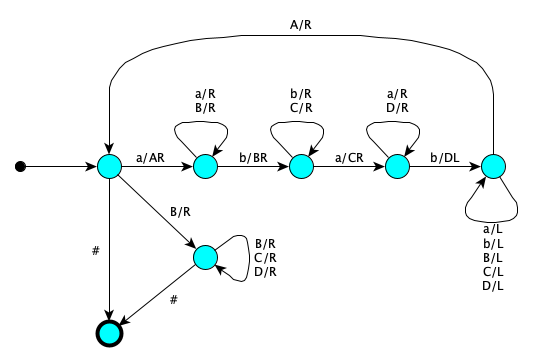
Turing Machine transducers:

1. $\lambda n. 2n + 2$. Idea is to first increment, then double.

   

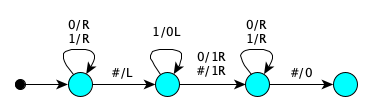
   State	Symbol	Actions	Next
   GoingToEnd	$0$	Right	GoingToEnd
   GoingToEnd	$1$	Right	GoingToEnd
   GoingToEnd	$\#$	Left	Flipping1sToIncrement
   Flipping1sToIncrement	$1$	Print $0$, Left	Flipping1sToIncrement
   Flipping1sToIncrement	$0$	Print $1$, Right	Incremented
   Flipping1sToIncrement	$\#$	Print $1$, Right	Incremented
   Incremented	$\#$	Print $0$	IncrementedAndDoubled

2. One's complement. Just flip all the bits as you move right.

   

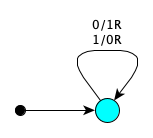
   State	Symbol	Actions	Next
   Flipping	$0$	Print $1$, Right	Flipping
   Flipping	$1$	Print $0$, Right	Flipping

3. The function described in Python as lambda n: str(n)[1:-1]. This is done by ”erasing” the first and last symbols, i.e., writing over them with blanks.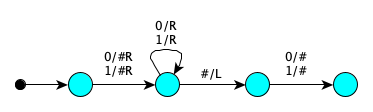

   

   State	Symbol	Actions	Next
   Start	$0$	Print $\#$, Right	FirstSymbolErased
   Start	$1$	Print $\#$, Right	FirstSymbolErased
   FirstSymbolErased	$0$	Right	FirstSymbolErased
   FirstSymbolErased	$1$	Right	FirstSymbolErased
   FirstSymbolErased	$\#$	Left	AtLastSymbol
   AtLastSymbol	$0$	Print $\#$	FirstAndLastSymbolErased
   AtLastSymbol	$1$	Print $\#$	FirstAndLastSymbolErased

The expression 5 * 3 - 1 ** 3 can be evaluated on a 3AC machine like this:

MUL 5, 3, r1
POW 1, 3, r2
SUB r1, r2, r0

and on a 0AC (stack) machine like this:

PUSH 5
PUSH 3
MUL
PUSH 1
PUSH 3
POW
SUB

Note that LOAD and PUSH are equivalent instructions.

1. $\{ a^ib^jc^k \mid i > j > k \}$ (c)
   This is not CF because when recognizing on a PDA, you push when you see an $a$, then pop when seeing $b$’s. You know there should still be $a$’s left after popping, but the number of marks remaining on the stack is only $i-j$. You don’t know how big $i$ and $j$ were, so there is no way to check $k$. It is obviously recursive since a trivial Python program can easily decide it by just counting.
2. $\{ a^ib^jc^k \mid i > j \wedge k \leq i-j \}$ (b)
   This is CF because when recognizing on a PDA, you push when you see an $a$, then pop when seeing $b$’s. You know there should still be $a$’s left after popping, and this number $i-j$. Pop when you see $c$’s and insure there is always something to pop. Also you can see the language is not regular since you have to remember the value of $i$, which is arbitrarily large.
3. $\{ \langle M \rangle \cdot w \mid M \textrm{ accepts } w\}$ (d)
   This is the classic language-acceptance problem whose proof that is r.e. but not recursive can be found in Sipser.
4. $\{ G \mid G \textrm{ is context-free} \wedge L(G)=\varnothing \}$ (d)
   Rice’s Theorem applies here.
5. $\{ a,b \}^*\{b\}^+$ (a)
   Walk the input from beginning to end and make sure it ends with a b. You might think you need to back up, but not so! Did you do the assigned reading in the Sipser and Berhardt books?
6. $\{ \langle M\rangle \mid M \textrm{ does not halt }\}$ (e)
   A well-known result. This was on the course notes for computability!
7. $\{ w \mid w \textrm{ is a decimal numeral divisible by 7} \}$ (a)
   A Finite Automata can track the remainder as digits are added.
8. $\{ www \mid w \textrm{ is a string over the Unicode alphabet} \}$ (c)
   Not context free since the $ww$ language is not even context free! But definitely recursive as you can split the string into three parts and just check in a way you will always finish.