const regexes = {
  canadianPostalCode: /^[A-CEGHJ-NPR-TV-Z]\d[A-CEGHJ-NPR-TV-Z] \d[A-CEGHJ-NPR-TV-Z]\d$/,
  visa: /^4\d{12}(\d{3})?$/,
  masterCard:
    /^(5[1-5]\d{14}|222[1-9]\d{12}|22[3-9]\d{13}|2[3-6]\d{14}|27[01]\d{14}|2720\d{12})$/,
  notThreeEndingInOO: /^(?![\p{L}]oo$)\p{L}*$/iu,
  divisibleBy16: /^(0{1,3}|[01]*0000)$/,
  eightThroughThirtyTwo: /^([89]|[12]\d|3[0-2])$/,
  notPythonPycharmPyc: /^(?!pyc$|python$|pycharm$)\p{L}*$/u,
  restrictedFloats: /^\d+(\.\d*)?(e[+-]?\d{1,3})?$/i,
  palindromes2358:
    /^(?:([abc])\1|([abc])[abc]\2|([abc])([abc])[abc]\4\3|([abc])([abc])([abc])([abc])\8\7\6\5)$/,
  pythonStringLiterals:
    /^([ruf]|fr|rf)?('([^'\n\\]|\\.)*'|"([^"\n\\]|\\.)*"|'''('(?!'')|[^'\n\\]|\\.)*'''|"""("(?!"")|[^"\n\\]|\\.)*""")$/i,
}

export function matches(name, string) {
  return regexes[name].test(string)
}

C Function:

int f(const int n) {
  return n % 2 == 0 ? n / 2 : 3 * n + 1;
}

WebAssembly:

(module
  (func $f (param $n i32) (result i32)
    (local.get 0)    ;; n
    (i32.const 3)
    (i32.mul)        ;; 3n
    (i32.const 1)
    (i32.add)        ;; 3n + 1
    (local.get 0)    ;; n
    (i32.const 1)
    (i32.shr_s)      ;; n / 2
    (local.get 0)    ;; n
    (i32.const 1)
    (i32.and)        ;; odd(n)
    (i32.select)     ;; if n is odd, return 3n + 1, else return n / 2
  )
)

x86-64 Assembly:

.section .text
.global f
f:
        mov     ecx, edi               ; ecx = n (parameter is in edi)
        sar     ecx                    ; ecx = n / 2
        test    dil, 1                 ; dil = is_odd(n)
        lea     eax, [rdi + 2*rdi + 1] ; eax = 3n + 1
        cmovz   eax, ecx               ; if is_odd(n) then eax = n / 2
        ret                            ; return eax

Assume $EQ$ is decidable. Then there exists an always-halting TM that inputs two descriptions and outputs YES if the machines recognize exactly the same language and NO otherwise.

Now let’s define a function, $T$ that when given a machine description $\langle M\rangle$ and a string $w$, produces a machine that erases its input and replaces it with $w$, then simply runs $M$ (with input $w$). Thus $L(T(\langle M\rangle, w))$ is $\{w\}$ if $M$ halts on $w$ and is $\varnothing$ otherwise.

Now, there exists a very simple machine $REJECT\_ALL$ (you should be able to show it, it is so simple) that rejects (says NO to) all of its inputs. Note that $L(REJECT\_ALL) = \varnothing$.

Now here’s the good stuff. We’re going to make a machine that inputs some $\langle M\rangle$ and $w$, then we are going to run $EQ$ on $T(\langle M\rangle, w)$ and $REJECT\_ALL$. Then, if this run says YES, our new machine will say NO, and vice versa. WE’VE JUST DECIDED THE HALTING PROBLEM, PEOPLE. But the halting problem is undecidable, so our assumption that $EQ$ was decidable must have been incorrect. Therefore $EQ$ is undecidable.

A picture might help:

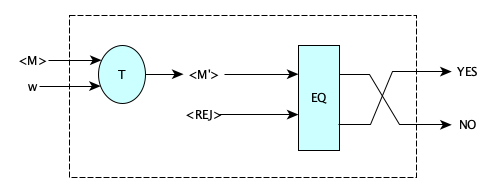
Remember, in this diagram $L(M') = \varnothing$ iff $M$ does not halt on $w$, so the dashed box would indeed be a halting problem decider if $EQ$ were a decider.