The easy problem is to explain the physical mechanisms in the brain that underlie conscious versus unconscious behavior.

The hard problem is to explain how (and why) it is we have subjective, qualitative experiences; in other words, why things feel a certain way. Many people think it may not be solvable since qualitative experience does not appear to be reducible to anything else, and hence not describable in a computational sense.

Dennett does not believe the hard problem exists, because in his view subjective experience is indeed the result of mental computation, and explaining the workings of the brain (solving the easy problem) explains qualia as well — there is nothing "left over" once the easy problem is solved. In other words, the hard problem is as easy as the hard problem.

Searle, on the other hand, says that the easy problem is as hard as the hard problem, because not only is consciousness not reducible, neither is intentionality (from Curtis Brown).

Until Gödel, many people assumed that mathematical logic was all that. But it ain't. Many people thought that formal systems, with their axioms and rules, could generate all mathematical truths. But they can't even generate, Gödel showed in his First Incompleteness Theorem, all the truths of basic arithmetic on nonnegative integers. The Second Incompleteness Theorem was a big deal, too: it said a formal system can't prove its own consistency (unless it is inconsistent). That probably really bummed Hilbert out. It made people wonder what it would take to show arbitrarily powerful systems of mathematics to be consistent. If you can't be sure of the consistency of your system, then what have you got?

Self-swallowing sets:

• The set of all things I am thinking about as I wrote this answer
• The set of all things you are reading now
• The set of all things except Lake Tahoe
• The set of all things that can be described in English in less than 4000 words
• The set containing the five sets in this answer

Autological words: writable, used, common, readable, definable.

Heterological words: French, purple, monosyllabic, misspelled, wet.

1. If you don't leave now, you will not win the prize.

   ~l → ~w       -- I'm not too thrilled with this answer, but it is fine for now

2. Ani or her sisters might have been late.

   ◊P(La ∨ ∀p.(Sap ⊃ Lp))

3. Some dogs like cats who live in the capital of Turkey.

   ∃d.(∀c.(Lc(℩c'.Ctc') ⊃ L'dc))

4. The person who won the race prefers orange juice to tea.

   P(℩p.Wp)ot

5. 3 will never be greater be 7.

   G(~ (3 > 7))

   or

   ~F(3 > 7)

6. Not every odd number is greater than its own square.

   ~∀x.(Ox ⊃ x > x*x)

   or

   ∃x.(Ox ∧ ~(x > x*x))

7. Something evil caused all evil things except itself.

   ∃x. (Ex ∧ ∀y. (Ey ∧ ~(y=x)) ⊃ Cxy)

8. Some day, it will be possible that all players will have the same score.

   F◊∃s.(∀p.Sps)

9. War is peace, freedom is slavery, and ignorance is strength.

   (w = p) ∧ (f = s) ∧ (i = s')

10. All that was once true will someday necessarily be forever false.

    ∀Q.(PQ ⊃ F◻G(~Q))       -- tricky... this is a higher-order formula

The sentence "If x+1=8 then x must be 7" is ambiguous. It is only true when the modality "must be" applies to the conditional itself and false when it applies just to the consequent. Why? Because in all possible worlds, x+1=8 implies x=7 (i.e. ◻x+1=8 → x=7), but it is certainly not true that just because x+1=8 in this world doesn't mean that x=7 in all possible worlds. There could be another world in which x+1=9 and x=8.

One way to phrase these different meanings in English is:

• It is necessarily the case that: if x + 1 = 8 then x = 7
• If x + 1 = 8, then it is necessary and irrevocably true that, in all possible worlds, x = 7.

One way is to claim that while Harry Potter, Santa Claus, Pegasus and Noah do not or did not exist as physical beings in our world, for each of them the idea or symbol of the being does exist. So Russell would accept the statement as true, since we now have existence, albeit of an idea rather than of a physical manifestation.

A second way is to throw out the need for existence when using a descriptor, and define your system of logic so that the descriptor stands for some unspecified object with the desired property, only you can't really say anything about the object at all, not even that it exists. That is, if your logic had a rule saying "if x has wings then x has wings" then you would have "The biggest winged horse has wings" as true, but you could not derive from that theorem than the biggest winged horse exists.

Well, many answers are possible here. The trick is to just place four more formulas on the diagram. The question wasn't very well phrased since you can't really say what the next four are. Here is one possible answer out of many:

Let d = you have the disease and p = you tested positive. We know pr(d) = 0.00003 and pr(p|d) = 0.98. What is pr(p)? Suppose there are N people in the population. 98% of 0.00003N people with the disease will test positive, and 2% of the 0.99997N people without the disease will test positive. So pr(p) = (0.98(0.00003)N + 0.02(0.99997N)) / N = 0.0200288. Now we can use the formula for inverse probabilities:

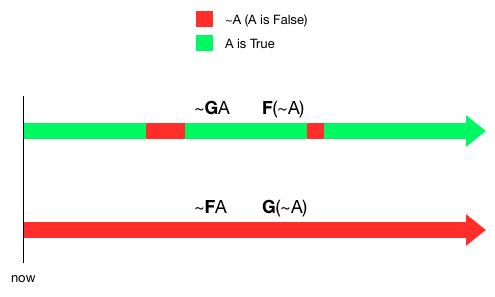
pr(d|p) = pr(p|d) * pr(d) / pr(p)
         = 0.98 * 0.00003 / 0.0200288
         ≈ 0.00147

Yes. ~FA ≡ G(~A) is true: it expresses the equivalence of "It is not true that A will be true at some point in the future" and "It will always be the case from now on that A is not true." Furthermore, ~GA ≡ F(~A) is true: it expresses the equivalence of "It is not true that A will be now and forever true" and "There will be some time in the future that A will be not true."