CMSI 2310: Language, Thought, and Computation Practice Questions

This page of questions is not complete. It is, however, to the best of my knowledge, consistent, although I can not prove it to be so.

What is the central question explored in GEB?
What is a strange loop?
Describe fugues and canons.
Name four ways to create a transformed copy of a theme in a canon.
How are Escher’s Waterfall and Print Gallery similar? How are they different?
Why was Gödel’s use of a self-referential statement in his incompleteness proof surprising to Russell?
What are some of the arguments commonly given for computers not being able to originate or create anything (i.e., for the impossibility of programming intelligence)? What are the common counter-arguments?
Give five examples of self-swallowing sets, five examples of autological words, and five examples of heterological words (other than those in the course readings or lectures to date).
What is Zeno’s Paradox? How is it reconciled, or “solved”? Do any philosophers today think that it is still “unsolved”? Are there any mathematicians on record as believing it “unsolved”?
What are formal systems and why do mathematicians bother with them?
Give a derivation of MUIUUIUUIIU in the MIU-system.
Discuss Hofstadter’s claim that it is “possible for a machine to act unobservant [but] impossible for a human to act unobservant.”
Why should the set of axioms in a formal system be decidable?
Prove or disprove: if a given formal system does not have any shortening rules, then theoremhood in the system is decidable.
State precisely what it is that the Tortoise is refusing to accept in the Two Part Invention. Is this concept one of logic or metalogic? Explain.
Is -p--p-q---- a theorem of the pq-system? If so, give a derivation (proof). If not, why not? And why might some humans think that it is?
What is needed for the meaningless symbols of a formal system to acquire meaning?
How is the notion of $\infty$ captured in Euclid’s proof that there is no largest prime number?
What is meant by figure and ground in
1. Art
2. Music
3. Formal Systems in general, and of number theory in particular
What is the meaning of a formal system that is recursively enumerable but not recursive?
Characterize the sequence of integers (from GEB) 1 3 7 12 18 26 35 45 56 69.... How are the notions of figure and ground intertwined here?
Give formal systems for
1. (Non-negative) Binary numerals divisible by 4
2. (Non-negative) Binary numerals not divisible by 4
How is Hofstadter’s Contracrostipunctus an acrostic? How is it self-referential?
How did the Tortoise show, in Contracrostipunctus, that there is no such thing as a perfect record player? How is this related to Gödel’s demonstration that there is no perfect formal system for number theory?
What is meant by the statement that consistency is not an inherent property of a formal system?
What is the Zen, or U-Mode, interpretation of Escher’s Relativity?
How is consistency restored to the pq-system after the addition of the axiom xp-qx? That is, what is the change of interpretation?
If a formal system is found to be incomplete (with respect to an interpretation), what can you do to try and restore completeness?
In Hofstadter’s Little Harmonic Labyrinth, is GOD a djinn? Why or why not?
Why was Achilles able to get a meta-wish, despite having his request for one passed sequentially through an infinite chain of genies?
Why did Achilles’ wish (“I wish my wish would not be granted”) in Little Harmonic Labyrinth cause an indescribable event to occur?
How does the discussion about tonic in Little Harmonic Labyrinth relate to the dialog itself?
What is the difference between a recursive definition and a circular definition?
Write recursive and non-recursive generator functions, in the programming language of your choice, for the following functions from GEB:
1. The function G over natural numbers, defined thusly:
```
    G(0) = 0
    G(n+1) = n+1 - G(G(n))
```
2. The functions M and F over natural numbers, defined thusly:
```
    M(0) = 0
    F(0) = 1
    F(n+1) = n+1 - M(F(n))
    M(n+1) = n+1 - F(M(n))
```
3. The function Q over natural numbers, defined thusly:
```
    Q(1) = 1
    Q(2) = 1
    Q(n+2) = Q(n+2 - Q(n+1)) + Q(n+2 - Q(n))
```
Give recursive and non-recursive definitions of Ackermann’s function.
Prove that Ackermann’s function is recursive but not primitive recursive.
Write a program that generates random fancy nouns using the recursive transition networks from Chapter 5 of GEB.
Experiment with IFS generators. Create three (two-dimensional) IFS fractals that you find particularly cool and give the set of affine transformations that define them.
Write an application (browser-based is fine) for designing and rendering 2-D IFS fractals. Several of these exist on the web already, of course, but there is always room for improvement.
Give the set of affine transformations that the describe the following fractal. Also give the fractal dimension of this figure.
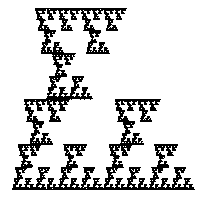
For the following fractal, give its fractal dimension, and an L-system to describe it.
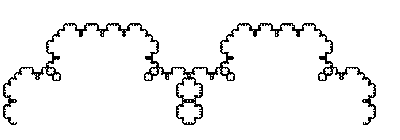
Give examples of exotic and prosaic isomorphisms besides those in GEB.
Do you see DNA as (1) meaningless without chemical context or as (2) containing such a compelling inner structure that it indeed describes a phenotype? Why?
Describe the three levels of information (the frame message, the outer message, and the inner message) contained in a movie, book, film, or work of art of your choice.
What is the significance of what Hofstadter calls “long genotypes”?
What logical rule of inference is the Tortoise refusing to employ in Chromatic Fantasy and Feud?

Match the formulas on the left with their descriptions on the right. Here $T(m,b,n)$ means monkey $m$ tosses banana $b$ to monkey $n$. This problem was created by Joel David Hamkins.

$\forall b \, \exists m \, \exists n\:T(m,b,n)$	maximal monkey madness
$\exists m \, \exists n \, \forall b\:T(m,b,n)$	monkey rugby
$\exists m \, \exists b \, \exists n\:T(m,b,n)$	leave no banana untossed
$\exists m \, \exists b \, \forall n\:T(m,b,n)$	one monkey really likes another
$\exists m \, \forall b \, \exists n\:T(m,b,n)$	a monkey plays zookeeper at lunchtime
$\exists m \, \forall b \, \forall n\:T(m,b,n)$	a monkey shows its banana to everyone
$\forall m \, \exists b \, \exists n\:T(m,b,n)$	a banana up in the air
$\forall m \, \exists b \, \forall n\:T(m,b,n)$	every monkey tosses every banana
$\forall m \, \forall b \, \exists n\:T(m,b,n)$	monkey quarterback practices tossing all the bananas, all monkeys catch
$\forall m \, \forall b \, \forall n\:T(m,b,n)$	delivery service monkey delivers all the bananas
$\exists m \, \forall n \, \exists b\:T(m,b,n)$	everyone, toss a banana to someone!
$\exists b \, \forall m \, \forall n\:T(m,b,n)$	monkey show and tell: every monkey shows their special banana to everyone

Give two examples, in English, of deductions that can be carried out in propositional logic that can not be carried out in syllogistic logic. Give two examples that than be carried out in syllogistic logic but not propositional logic.
Prove, in either Hofstadter’s formulation of the propositional calculus, or the formulation from my notes, that $(A \wedge B) \equiv (B \wedge A)$. (Note that Hofstadter does not use the $\equiv$ symbol, so prove both sides of the material implication.) How does this proof relate to your understanding of the Graham Priest’s example sentences “John hit his head and fell” and “John fell down and hit his head.”
What is the meaning of the Zen koan Gantō’s Ax?
Can the consistency of the propositional calculus be proven by reasoning only within the propositional calculus? Can the consistency of any formal system be proven within itself? If you don’t know the answer, that’s fine, but do you think, in principle that this should be the case? Or that it should not be the case? Why?
Prove the following theorems of the Propositional Calculus (you can use any reasonable formulation of the calculus—just state which one you are using). Also, give the translation of each formula into English, assuming $p$ stands for “This mind is Buddha” and $q$ stands for “The moon is shining on the lake.”
1. $(p \Rightarrow (q \Rightarrow p))$
2. $(p \Rightarrow (q \vee ~q))$
3. $((p \wedge ~p) \Rightarrow q)$
4. $((p \wedge ~p) \Rightarrow ~q)$
5. $((p \Rightarrow q) \vee (q \Rightarrow p))$
Define the following in the context of TNT: variable, atom, term, formula, sentence, predicate, free variable, open formula, closed formula, bound variable.
Express the following in TNT notation:
1. 8 is not the square of 3.
2. 8 is not the square of any number.
3. 53 is odd.
4. There are no solutions to $a^n+b^n=c^n$ where $n \gt 2$.
5. There are infinitely many prime numbers.
6. Every number has a successor.
7. There is a least number.
8. Every even prime is the sum of two numbers.
9. Every even number is the sum of two primes.
10. There is a number n such that $3n+1$ is prime.
Give a proof that $1+1=2$ in TNT. If you have a copy of Principia Mathematica, locate Russell and Whitehead’s proof of this theorem. Why is the TNT proof shorter?
Explain, in technical detail, why you cannot use the rule of specialization to go from ∀a:∃b:b=Sa to ∃b:b=Sb.
What is ω-incompleteness? ω-inconsistency?
Prove, in TNT, the following:
1. ∃a:a=SSSSa
2. ∀a:(a+S0)=Sa
3. ∀a:(S0+a)=Sa
4. ∀a:a=a
5. ∀a:(a•S0)=a
Why is it that if TNT were complete, then all boolean-valued questions of number theory could be resolved by machine?
Who was David Hilbert? What was Hilbert’s program?
In what sense does Gödel’s result that any system strong enough to prove that TNT is consistent must be at least as strong as TNT make us somewhat unsure that TNT really is consistent?
Write a short essay on Zhàozhōu Cōngshěn (趙州從諗), a.k.a. Jōshū.
Read five kōans from The Gateless Gate For each, identify the preconceptions you are being drawn to discard while practicing the kōan.
For each of the following questions, explain whether the answer “Mu” (or “Wu” (無)) is appropriate, and why:
1. Are you still beating your wife?
2. Is the proposition “this sentence is true” true?
3. Who is the King of France?
4. Where did you hide the murder weapon?
5. Has a dog Buddha nature or not?
In A Mu Offering, what aspect of formal systems underlies the Tortoise’s question of whether it is possible to make strings that don’t have Buddha-nature? What aspect underlies his question of whether certain strings with Buddha-nature cannot be made by following the Rules of Zen strings?
Why did tying an extra knot and the end of the Tortoise’s string in A Mu Offering cause this knot and the already existing knot next to it to disappear? What would an intuitionist say about this?
Explain how Mumon’s statement “It cannot be expressed with words and it cannot be expressed without words” is isomorphic to the mathematician’s dilemma regarding formal systems. Does this give credence to the idea that words and truth are incompatible?
(This question is asked but not answered by Hofstadter himself.) What would it have meant, and would it have made any difference, if Nansen’s response to a monk’s question of whether there exists a teaching that no master ever taught before was “no” instead of “yes”?
What do you make of the argument that humans have trouble transcending dualism (i.e., achieving enlightenment) because our use of formal systems and categorization in general is hard-wired (or at least expressed at some very low-level inaccessible layer of the mind)? Supposing that these dualistic phenomena are indeed hard-wired, does this necessarily mean we can never be enlightened? Why or why not?
Find research articles in neuroscience or behavioral sciences that attempt to explain how people act when trying to process paradoxes such as the Barber paradox or the Grelling-Nelson paradox. Relate the findings of these articles to aspects of logic or Zen with which you are familiar.
Are logic and enlightenment compatible? If so, under what assumptions? If not, why not? Consider the way certain systems of logic deal with, or do not deal with, paradoxes.
Consider this quote from GEB: “[The] master wants to get across the idea that an enlightened state is one where the borderlines between the self and the rest of the universe are dissolved.” Is such a state possible? Does the fact that we can describe or imagine such a state (using words!) have anything to do with this question? Consider Jill Bolte Taylor’s experience in this video in your answer.
How the spheres in the Escher drawing Three Spheres II like people in the sense of I am a Strange Loop. If you haven’t read that book, you can get an overview of some of its main themes in this interview with Hofstadter.
Is MIIUIUI a theorem of the MIU-system? Why or why not?
Explain in your own words, why the study of all formal systems, regardless of how simple or complex they are, can be studied in plain number theory.
What are the limitations of formal systems?
Give a Gödel numbering for the pq-system, and code its axioms and rules of interest in number-theoretic terms, in the manner in which the MIU-system was coded in Chapter 9 of GEB.
Give an isomorphism between the central dogma of mathematical logic and the central dogma of molecular biology.
Explain, in as much detail as you can, why the TNT-numbers comprise a recursively enumerable set.
Recall the statement G, from TNT, the statement that asserts its own non-theoremhood. Explain, in detail, the following statement: “If G were a theorem, then TNT would be inconsistent; if G were not a theorem, then TNT would be incomplete.”
Hofstadter uses the example of a person’s ability to see a picture of a face from pixels on a screen and later remarks that “intelligence depends crucially on the ability to create high-level descriptions of complex arrays, such as chess boards, television screens, printed pages, or paintings.” Daniel Dennett, in this video, uses a similar example — how blobs of paint or pixellated images are interpreted at a higher level. But what is Dennett trying to explain with these examples?
How are computer programs chunked? Give examples using functions, classes, and modules in your answer.
Why does Hofstadter remark that it is somewhat surprising that that programs written in languages at a higher level than machine language can said to be running at all?
What is interesting about the fact that human language acquisition eventually reaches some critical point after which the human can use language to acquire new language? What are some isomorphisms between this phenomenon and other phenomena in GEB?
What concepts are behind the question of whether computers are super flexible or super rigid?
Is it possible to design a programming language that truly admits some “imprecision” suggestive of the human ability to compensate for certain things like misspellings? Could such a language ever be said to operate outside its own rules? If so, how? If not, is there a way in which it could appear to?
Do you find it surprising that the fixed hardware of the brain (with a non-reprogrammable machine language of its own) can give rise to minds? Why or why not?
Why do people tend to confuse the statements “computers can only do what you tell them to do” and “computers cannot think”? Why are they actually fundamentally different?
Give three examples each of systems whose components have a canceling effect on each other and systems whose components’ behavior have huge high-level consequences.
What are epiphenomena? Give five examples other than those given in GEB (e.g., pressure, temperature).
Define holism and reductionism. Why does the Crab in Ant Fugue reject reductionism? Why does the Anteater reject holism?
What is the difference between Achilles’ MU and the Tortoise’s MU in Ant Fugue?
Why does Achilles (in Ant Fugue) have trouble with the relationship of ants to ant colonies being like that of neurons to brains?
Define signals, symbols, passive symbols, and active symbols. Relate these concepts to ant colonies, language, and the brain, using the notions of levels of description, critical mass (regarding the formation of signals), and purposeful behavior. At what level do conscious systems operate?
Identify the fermata, stretto and organ point in the dialogs Prelude and Ant Fugue.
Why is it that the mind has an easy time intermingling fact and fantasy? (Answer in terms of Hofstadter’s descriptions of intensionality and extensionality.)
What are the roles of the cerebellum and the cerebral cortex?
Are symbols in the brain fixed or variable? Why?
Give ten examples of class symbols and instance symbols. How are these concepts related to programming?
What are the arguments for and against intelligence being “brain-bound” as opposed to a phonomena liftable from lower-levels? Who are the principal proponents of the different viewpoints?
Search the web for simulations of ant colonies, swarms, or other examples of collective behavior. Experiment with them. Make a simple one of your own.
What experiments exist to show that many non-human animals’ understanding of how to carry out tasks such as tending nests, raising young, and so on is not what we might call “understanding” at all?
How are imaginary worlds of dreams, fantasies, and hallucinations similar to, and different from, what we call reality?
What is the difference between declarative and procedual knowledge? Give five examples of each.
Do some research into theories of how the human brain stores knowledge of certain songs, or melodies. Also lookup and study audio formats like .wav and MP3. How are these file formats similar to and different from the ways in which the brain might store and recall melodies?
What are (a) the easy problem of consciousness, and (b) the hard problem of consciousness? What do (c) Colin McGinn and (d) Daniel Dennett think of these problems?
Contrast the views of Tom Wolfe and Steven Pinker on how society would react to a conclusive proof that consciousness is a locatable activity in the brain.
What motivates J.R. Lucas to think that Gödel’s theorems even suggest that a mind is superior to a computing machine? What do you make of the passage from his article Minds, Machines, and Gödel quoted on pages 388-390 of GEB?
State, in your own words, the difference between the Goldbach and Tortoise properties of natural numbers, from a computational perspective.
In Aria with Diverse Variations, Achilles makes the claim that it “never takes an infinite number of reasons to account for some arithmetical truth.” What motivates him to make this claim? Is it true?
What is the significance of the language BlooP?
Translate Hofstadter’s TWO-TO-THE-THREE-TO-THE BlooP procedure into Ruby or Python. If you choose Ruby, use the times method.
Hofstadter defines a primitive recursive function as any function that can be computed by a BlooP procedure. Find a more rigorous mathematical definition (Wikipedia has one, of course). Argue why this definition is equivalent to Hofstadter’s.
Explain in detail, in your own words, why the Ackermann function is total recursive but not primitive recursive.
Do the 18 exercises in GEB, pages 415-417. That is, for each of the 18 predicates and functions, state whether each is primitive recursive (BlooP-computable) or not, and why.
Write, in Python or Ruby, the predicates PRIME?, TRIVIAL?, TORTOISE-PAIR?, TORTOISE?, MIU-WELL-FORMED?, MIU-PROOF-PAIR?, and MIU-THEOREM?.
Hofstadter claims in GEB, page, 417, that TNT can “express virtually any number-theoretic property.”
1. Express each of the predicates defined on page 416 in TNT. (If any predicate seems to hard to physically express, define how you would go about constructing a TNT formula for it.)
2. What does Hofstadter mean by “virtually” here? Does he mean there are number-theoretic properties that cannot be expressed in TNT? If so, give one.
Is the predicate FERMAT representable in TNT? Why or why not?
Why is it that the diagonalization method can be called “insiduously repeatable”?
As of January, 2018, the question of whether all numbers are wondrous (the Collatz Conjecture) remains unsolved. What is the greatest number $n$ known so far such that all natural numbers below $n$ are wondrous? Why does the fact that this number seems large to us mean nothing to the truth of falsity of the conjecture?
Describe, in your own words, the Polya and Mertens conjectures. Each of these conjectured that property held for all natural numbers, but they were later shown to have counterexamples. What is the smallest counterexample for each conjecture?
How is a program computing a partial recursive function, operating on a nasty input that causes an infinite loop, like answering a question “Mu”?
Make a list of ideas that have appeared in print or on the web that can qualify at misapplications of Gödel’s theorems. You can start your list by reading this book review by Panu Raatikainen.
Why is the first word in GEB “Author”? Why is this question the last question on this web page?