CMSI 2120: Data Structures: Homework #5 Answers

NeedlesslyRecursive.java

import static java.math.BigInteger.ONE;
import static java.math.BigInteger.ZERO;
import java.math.BigInteger;

/**
 * Some functions written recursively only for illustrative purposes.
 */
public interface NeedlesslyRecursive {

    static String binaryString(int x) {
        if (x == Integer.MIN_VALUE) {
            return "-10000000000000000000000000000000";
        } else if (x < 0) {
            return "-" + binaryString(-x);
        } else if (x < 2) {
            return "" + x;
        } else {
            return binaryString(x / 2) + binaryString(x % 2);
        }
    }

    static BigInteger a(BigInteger x, BigInteger y) {
        if (x == null || y == null || x.compareTo(ZERO) < 0 || y.compareTo(ZERO) < 0) {
            throw new IllegalArgumentException("Negative arguments not allowed");
        } else if (x.equals(ZERO)) {
            return y.add(ONE);
        } else if (y.equals(ZERO)) {
            return a(x.subtract(ONE), ONE);
        } else {
            return a(x.subtract(ONE), a(x, y.subtract(ONE)));
        }
    }

    static int log3(int n) {
        if (n <= 0) {
            throw new IllegalArgumentException();
        } else if (n < 3) {
            return 0;
        } else {
            return 1 + log3(n / 3);
        }
    }

    static BigInteger power(BigInteger x, int n) {
        if (n <= 0) {
            return ONE;
        } else if (n % 2 == 0) {
            return power(x.multiply(x), n / 2);
        } else {
            return power(x.multiply(x), n / 2).multiply(x);
        }
    }
}

To figure out $A(4,2)$, we should work our way up to finding a general solution to $A(4,y)$. If you run a program which computes the value via the usual recursive formulation of the function, it will never terminate in your lifetime. Therefore we have to resort to some cleverness if finding alternate (but equivalent) definitions for the function.
$A(0,y) = y+1$, by definition

$A(1,0) = A(0,1) = 2$
For $y > 0$, $A(1,y) = A(0,A(1,y-1)) = A(1,y-1)+1$
$A(1,*) = [2,3,4,5,6,7, \ldots]$
$A(1,y) = y+2$

$A(2,0) = A(1,1) = 3$
For $y > 0$, $A(2,y) = A(1,A(2,y-1)) = A(2,y-1)+2$
$A(2,*) = [3,5,7,9,11,\ldots]$
$A(2,y) = 2y+3$

$A(3,0) = A(2,1) = 5$
For $y > 0$, $A(3,y) = A(2,A(3,y-1)) = 2(A(3,y-1))+3$
$A(3,*) = [5, 13, 29, 61, 125, \ldots]$
$A(3,y) = 2^{n+3} - 3$

$A(4,0) = A(3,1) = 2^4-3 = 13$
For $y > 0$, $A(4,y) = A(3,A(4,y-1)) = 2^{A(4,y-1)+3}-3$
$A(4,1) = 2^{A(4,0)+3}-3 = 2^{13+3}-3 = 2^{16}-3 = 65533$
$A(4,2) = 2^{A(4,1))+3}-3 = 2^{65533+3}-3 = \boxed{2^{65536}-3}$
The naive recursive algorithm in the best case is a base case, with best case complexity function $\Theta(1)$. In the worst case, we make 2 calls at level $n$, 4 calls at level $n-1$, 8 calls at level $n-2$, and so on. The calls may be overlapping, but they are still made. The number of calls is $2+4+8+16+32+\ldots$ which is $\boxed{\Theta(2^n)}$.
The non-recursive formulation leads to the computation $\frac{n(n-1)(n-2)\cdots(n-k+1)}{k(k-1)(k-2)\cdots 1}$. This is $2k$ multiplications. If all values fit in a single word of memory, the complexity is $\boxed{\Theta(k)}$. If these are big integers, then the complexity is a function of the bit length, which is exponential in $k$.

Selection Sort

81 9 17 21 20 8 2 5 1 83 23
1|9 17 21 20 8 2 5 81 83 23
1 2|17 21 20 8 9 5 81 83 23
1 2 5|21 20 8 9 17 81 83 23
1 2 5 8|20 21 9 17 81 83 23
1 2 5 8 9|21 20 17 81 83 23
1 2 5 8 9 17|20 21 81 83 23
1 2 5 8 9 17 20|21 81 83 23
1 2 5 8 9 17 20 21|81 83 23
1 2 5 8 9 17 20 21 23|83 81
1 2 5 8 9 17 20 21 23 81|83

Gnome Sort

81 9 17 21 20 8 2 5 1 83 23
81.9 17 21 20 8 2 5 1 83 23
9 81.17 21 20 8 2 5 1 83 23
9 17 81.21 20 8 2 5 1 83 23
9 17 21 81.20 8 2 5 1 83 23
9 17 21.20 81 8 2 5 1 83 23
9 17.20 21 81 8 2 5 1 83 23
9 17 20 21 81.8 2 5 1 83 23
9 17 20 21.8 81 2 5 1 83 23
9 17 20.8 21 81 2 5 1 83 23
9 17.8 20 21 81 2 5 1 83 23
9.8 17 20 21 81 2 5 1 83 23
8.9 17 20 21 81 2 5 1 83 23
8 9 17 20 21 81.2 5 1 83 23
8 9 17 20 21.2 81 5 1 83 23
8 9 17 20.2 21 81 5 1 83 23
8 9 17.2 20 21 81 5 1 83 23
8 9.2 17 20 21 81 5 1 83 23
8.2 9 17 20 21 81 5 1 83 23
2 8 9 17 20 21 81.5 1 83 23
2 8 9 17 20 21.5 81 1 83 23
2 8 9 17 20.5 21 81 1 83 23
2 8 9 17.5 20 21 81 1 83 23
2 8 9 17.5 20 21 81 1 83 23
2 8 9.5 17 20 21 81 1 83 23
2 8.5 9 17 20 21 81 1 83 23
2.5 8 9 17 20 21 81 1 83 23
2 5 8 9 17 20 21 81.1 83 23
2 5 8 9 17 20 21.1 81 83 23
2 5 8 9 17 20.1 21 81 83 23
2 5 8 9 17.1 20 21 81 83 23
2 5 8 9.1 17 20 21 81 83 23
2 5 8.1 9 17 20 21 81 83 23
2 5.1 8 9 17 20 21 81 83 23
2.1 5 8 9 17 20 21 81 83 23
1 2 5 8 9 17 20 21 81 83.23
1 2 5 8 9 17 20 21 81.23 83
1 2 5 8 9 17 20 21.23 81 83
1 2 5 8 9 17 20 21 23 81 83

Insertion Sort

81 9 17 21 20 8 2 5 1 83 23
9 81|17 21 20 8 2 5 1 83 23
9 17 81|21 20 8 2 5 1 83 23
9 17 21 81|20 8 2 5 1 83 23
9 17 20 21 81|8 2 5 1 83 23
8 9 17 20 21 81|2 5 1 83 23
2 8 9 17 20 21 81|5 1 83 23
2 5 8 9 17 20 21 81|1 83 23
1 2 5 8 9 17 20 21 81|83 23
1 2 5 8 9 17 20 21 81 83|23
1 2 5 8 9 17 20 21 23 81 83

Quicksort with first element as pivot
(will do this later)

Mergesort

81 9 17 21 20 8 2 5 1 83 23
9 81|17 21|8 20|2 5|1 83|23
9 17 21 81|2 5 8 20|1 23 83
2 5 8 9 17 20 21 81|1 23 83
1 2 5 8 9 17 20 21 23 81 83

Heap Sort

81 9 17 21 20 8 2 5 1 83 23   -> sift 20 down
81 9 17 21 83 8 2 5 1 20 23   -> sift 21 down
81 9 17 21 83 8 2 5 1 20 23   -> sift 17 down
81 9 17 21 83 8 2 5 1 20 23   -> sift 9 down
81 83 17 21 23 8 2 5 1 20 9   -> sift 81 down, completes heapification
83 81 17 21 23 8 2 5 1 20 9   -> swap 83 to end, sift 9 down
81 23 17 21 20 8 2 5 1 9|83   -> swap 81 to end, sift 9 down
23 21 17 9 20 8 2 5 1|81 83   -> swap 23 to end, sift 1 down
21 20 17 9 1 8 2 5|23 81 83   -> swap 21 to end, sift 5 down
20 9 17 5 1 8 2|21 23 81 83   -> swap 20 to end, sift 2 down
17 9 8 5 1 2|20 21 23 81 83   -> swap 17 to end, sift 2 down
9 5 8 2 1|17 20 21 23 81 83   -> swap 9 to end, sift 1 down
8 5 1 2|9 17 20 21 23 81 83   -> swap 8 to end, sift 2 down
5 2 1|8 9 17 20 21 23 81 83   -> swap 5 to end, sift 1 down
2 1|5 8 9 17 20 21 23 81 83   -> swap 2 to end, sift 1 down
1|2 5 8 9 17 20 21 23 81 83   -> swap 2 to end, 1 already in final place

Radix Sort

81 9 17 21 20 8 2 5 1 83 23
0:20 1:81,21,1 2:2 3:83,23 5:5 7:17 8:8 9:9
0:1,2,5,8,9 1:17 2:20,21,23 8:81,83
1 2 5 8 9 17 20 21 23 81 83

Exchange sorts swap elements according to some strategy until the list is sorted.

Insertion sorts repeatedly slide elements into a desired position.

Selection sorts repeatedly figure out which element to place into its final position.

Merge sorts repeatedly merge adjacent sorted sublists.

Distribution sorts don’t compare elements with each other, instead they (possibly repeatedly) distribute elements into different “buckets” from which the sorted output is is constructed.

Hybrid sorts combine two or more known techniques to sort.

Concurrent sorts take advantage of parallel hardware (and may perform terribly on sequential hardware).

Impractical sorts take longer than quadratic time, and often exponential or factorial time or worse, and do so generally for humorous effect.

Sets.java

import java.util.Set;
import java.util.HashSet;
import java.util.List;
import java.util.ArrayList;
import java.util.Collections;
import java.util.stream.Collectors;

public interface Sets {

    static <T> Set<Set<T>> powerSet(Set<T> set) {
        if (set.size() > 16) {
            throw new IllegalArgumentException("Set is too large");
        }
        var power = new HashSet<Set<T>>();
        power.add(new HashSet<>());
        for (var element : set) {
            var snapshot = Set.copyOf(power);
            for (var existing : snapshot) {
                var extended = new HashSet<T>(existing);
                extended.add(element);
                power.add(extended);
            }
        }
        return power;
    }

    // This is only one way to do it. We will see two others in class.
    static List<Integer> multiples(Set<Integer> set, int base) {
        var multiples = new ArrayList<Integer>();
        for (var element : set) {
            if (element % base == 0) {
                multiples.add(element);
            }
        }
        Collections.sort(multiples);
        return multiples;
    }

    // Another way to write this is as a one-liner where you simply return
    // set.stream().filter(x->x%base==0).sorted().collect(Collectors.toList());
}

For:
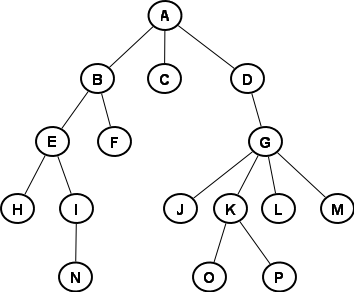
we have:
1. Size: 16
2. Number of edges: 15
3. Leaves: H N F C J O P L M
4. Children of D: G
5. Depth of G: 2
6. Degree of G: 4
7. Ancestors of G: D A
8. Descendants of G: J K L M O P
9. Nodes at level 3: H I J K L M
10. Height of the whole tree: 4
11. Width of the tree: 6
12. Height of D: 3
13. Simplest path from P to E: <P K G D A B E>
14. Degree of whole tree: 4
15. Breadth First: A B C D E F G H I J K L M N O P
16. Depth First: A B E H I N F C D G J K O P L M

There are 14 different binary trees of size 4. Only one of them is complete. The complete tree has the root marked "C". By the way, there's only one of them. There's only one complete $k$-ary tree of $n$ nodes for any given $k$ and $n$.

    •
   / 
  •
 /
•
 \
  •

  •
 / 
•
 \
  •
 /
•

  •
 / 
•
 \
  •
   \
    •

    •
   / 
  •
 / \
•   •

    •
   / \
  •   •
 /
•

  •
 / \
•   •
 \
  •

  •
 / \
•   •
   /
  •

  •
 / \
•   •
     \
      •

•
 \
  •
 / \
•   •

  •
   \
    •
   /
  •
 /
•

•
 \
  •
 /
•
 \
  •

•
 \
  •
   \
    •
   /
  •

•
 \
  •
   \
    •
     \
      •