(a,b) Trees
Definition
An (a,b) tree is a balanced (e.g. all leaves on same level) search tree in which:
- 2 ≤ a ≤ (b+1)/2
- Each internal node except the root has at least a children and at most b children.
- The root has at most b children.
An example of a (2,4)-tree:
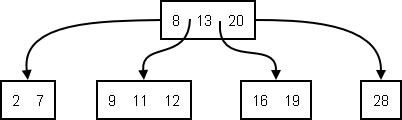
How They Work
Lookup
Lookup proceeds as in any search tree.
Insertion
Start by adding into the proper leaf node. If the addition causes an overflow (b items), then split and propagate the middle item.
Example: to insert 10 into the tree above:
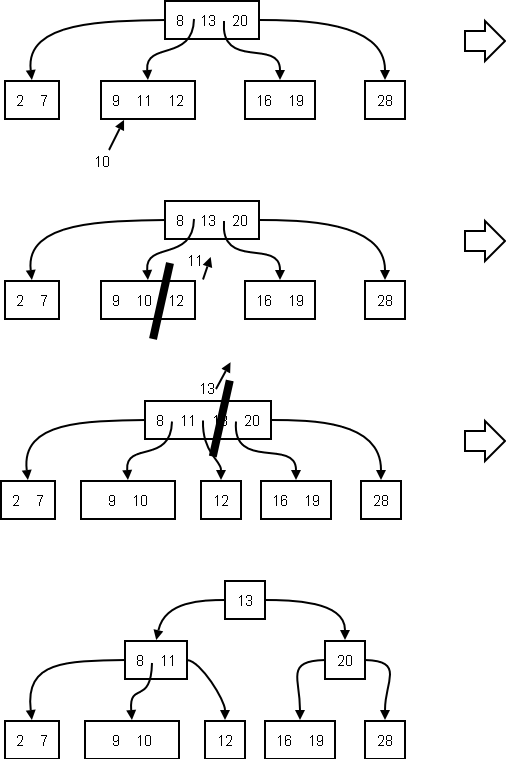
You should see from this why the root node allows for a minimum of two children (rather than a).
Deletion
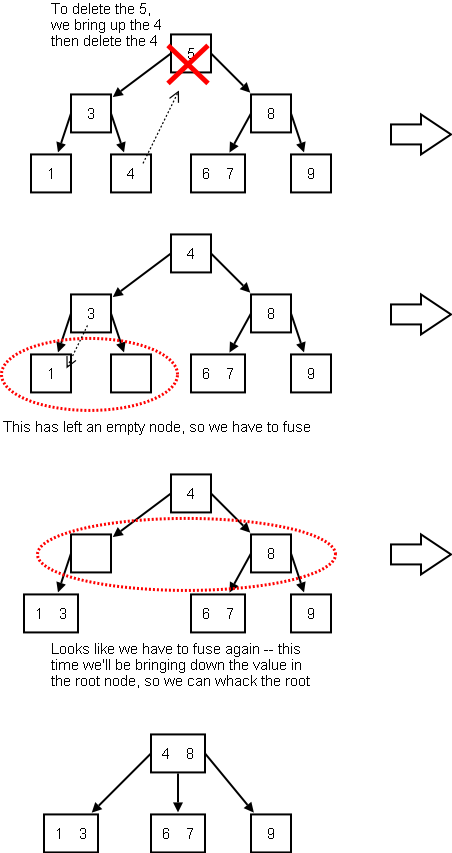
First, if the item you are deleting is not in a leaf node, then bring its predecessor up into its space and delete the predecessor item from its leaf node. This may require transfers and fusions. Fusions may cause underflow at the parent so in general this process has to be repeated up the tree.
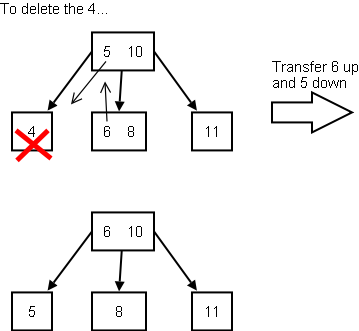
A simple deletion example, requiring transfers only:
A more complex example requiring multiple fusions:
B-Trees
A B-Tree is a (a,b)-tree with a = ceil(b/2).
The following are B-trees
- (2,3)-tree
- (2,4)-tree
- (3,5)-tree
- (3,6)-tree
- (4,7)-tree
- (4,8)-tree
- (5,9)-tree
- (5,10)-tree
A B+ tree is a cool variation of the B-tree. All elements are stored in the leaves; the internal nodes repeat keys where necessary. Also, the leaf nodes are chained together; this gives you rapid access to the entire collection in sorted order.
Summary
We’ve covered:
- What an (a,b) tree is
- How they work
- Variations on the (a,b) tree: B and B+ Trees