Algorithm Analysis

Introduction

It is important to be able to measure, or at least make educated statements about, the space and time complexity of an algorithm. This will allow you to compare the merits of two alternative approaches to a problem you need to solve, and also to determine whether a proposed solution will meet required resource constraints before you invest money and time coding.

Analysis

what you do before coding

Profiling (also called benchmarking)

what you do after the code is written.

Measuring Time

The absolute running time of an algorithm can never really be predicted, since this depends on the programming language used to implement the algorithm, the computer the program runs on, and many other factors. We need a machine-independent notion of an algorithm's running time.

What we usually can do is find a measure of an algorithm's relative running time, as a function of how many items there are in the input (technically, the number of symbols required to reasonably encode the input), often called n. The n could be

• The number of items in a container
• The length of a string or file
• The number of digits (or bits) in an integer
• The degree of a polynomial

We count the number of abstract operations as a function of n.

Example: Printing each element of an array

for (int i = 0; i < a.length; i++) {
    System.out.println(a[i]);
}

Here n = a.length (provided we know that all of the items in the array have a fixed size, which is often the case). We have

• 1 initialization of i
• n comparisons of i against a.length
• n increments of i
• n array indexing operations (to compute a[i])
• n invocations of System.out.println

so we write T(n) = 4n + 1... or should we?

All operations are not created equal. The printing completely overwhelms the increments, compares and indexing operations. We might as well talk about having n compare-index-print-increment operations. Then T(n) = n + 1. While we're at it, we might as well realize that initialization doesn't mean much, so we're safe to write T(n) = n.

Example: Multiplying two square matrices

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        double sum = 0;
        for (int k = 0; k < n; k++) {
            sum += a[i][k] * b[k][j];
        }
        c[i][j] = sum;
    }
}

Working from the inside-out we see each iteration of the k-loop has 4 array indexing operations, one multiplication, one addition, and one assignment. Or, heck, one big "sum += a[i][k]*b[k][j]" operation. Inside the j-loop there are n of these, together with an initialization of sum and an assignment to c[i][j]. Does this mean n+2? Hardly. Those other two operations don't count for much. By a similar argument we can ignore all the simple for-loop initializing, testing, and incrementing operations. They are fast. All we need to do is count the number of "sum += a[i][k]*b[k][j]" operations: that's really what counts.

So we have T(n) = n³.

But is this a fair measure of the complexity? We counted operations relative to the width of the matrices. We can also count operations relative to the number of items in the two matrices, which is 2n². Under this measure we'd say T(n) = n^1.5

Example: An Interesting Nested Loop

for (int i = 1; i <= n; i *= 2) {
    for (int j = 0; j < n; j++) {
        count++;
    }
}

Here the outer loop is done log n times and the inner loop is done n times, so T(n) = n log n. (Note that the default base for logarithms in Computer Science is 2.)

Example: Getting the value of the last element from an array

if (a.length > 0) {
    return a[a.length - 1];
} else {
    throw new NoSuchElementException();
}

Here n = a.length, and T(n) = 1.

Example: Addition

x + y

If x and y are primitive int values that each fit in a word of memory, any computer can add them in one step: T(n) = 1, But if these are BigInteger values, then what matters is how many digits (or bits) there are in each value. Since we just have to add the digits in each place and propagate carries, we get T(n) = n,

Example: Finding the index of a given value in an array

for (int i = 0; i < a.length; i++) {
    if (a[i] == x) {
        return i;
    }
}
throw new NoSuchElementException();

Here we need to introduce the B (best-case) and W (worst-case) functions: B(n) = 1 and W(n) = n. (What about the average case? It's usually difficult and sometimes impossible to compute an average case. You have to know something about the expected distributions of items.)

Time Complexity Classes

Comparison

To get a "feel" for the complexity classes consider a computer that performed one million abstract operations per second:

Is it just me or is there something about exponential time complexity?

Asymptotic Analysis

Since we are really measuring growth rates, we usually ignore:

• all but the "largest" term, and
• any constant multipliers

so for example

• λn. 0.4n⁵ + 3n³ + 253 behaves asymptotically like n⁵
• λn. 6.22n log n + n/7 behaves asymptotically like n log n

The justification for doing this is

• The difference between 6n and 3n isn't meaningful when looking at algorithms abstractly, since getting a computer that is twice as fast makes the former look like the latter.
• The difference between 2n and 2n+8 is insignificant as n gets larger and larger.
• If you are comparing the growth rates of, say, λn. n³ and λn. kn², the former will always eventually overtake the latter no matter how big you make k.

How can we formalize this? That is, how do we formalize things like "the set of all quadratic functions" or the "set of all cubic functions" or "the set of all logarithmic functions"?

Big-O: Asymptotic Upper Bounds

A function f is in O(g) whenever there exist constants c and N such that for every n > N, f(n) is bounded above by a constant times g(n).

O(g) = { f | ∃c N. ∀n>N. |f(n)| ≤ c|g(n)| }

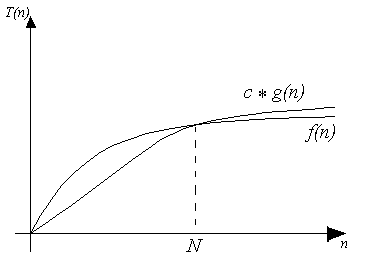
This means that O(g) is the set of all functions for which g is an asymptotic upper bound of f.

Examples

• λn. 0.4n⁵ + 3n³ + 253 ∈ O(λn. n⁵)
• λn. 6.22n log n + n/7 ∈ O(λn. n log n)

Notation

By convention, people usually drop the lambdas when writing expressions involving Big-O, so you will see things like O(n²).

Is Big-O Useful?

• Big-O notation is really only most useful for large n. The suppression of low-order terms and leading constants is misleading for small n. Be careful of functions such as
  • n² + 1000n
    
  • 0.0001n⁵ + 10⁶n²
    
  • 10^-42ⁿ + 10⁵n³
• Large constants on the more significant terms signify overhead, for example when comparing
  • 8n log n and 0.01n²
  note that the former is worse until n gets up to 10,710.
• Sedgewick writes "[Big-O analysis] must be considered the very first step in a progressive process of refining the analysis of an algorithm to reveal more details about its properties."
• Big-O is only an upperbound; it is not a tight upperbound. If an algorithm is in O(n²) it is also in O(n³), O(n¹⁰⁰), and O(2ⁿ). So it's not really right to say that all complexity functions in O(2ⁿ) are terrible, because that set properly includes the set O(1).

Big-Ω: Asymptotic Lower Bounds

There is a Big-Ω notation for lower bounds

A function f is in Ω(g) whenever there exist constants c and N such that for every n > N, f(n) is bounded below by a constant times g(n).

Ω(g) = { f | ∃c N. ∀n>N. |f(n)| ≥ c|g(n)| }

Lower bounds are useful because they say that an algorithm requires at least so much time. For example, you can say that printing an array is O(2ⁿ) because 2ⁿ really is an upper bound, it's just not a very tight one! But saying printing an array is Ω(n) means it requires at least linear time which is more accurate. Of course just about everything is Ω(1) so we like tight lower bounds too.

Big-Θ

When the lower and upper bounds are the same, we can use Big-Theta notation.

Θ(g) = { f | ∃c₁ c₂ N. ∀n>N. c₁|g(n) ≤ |f(n)| ≤ c₂|g(n)| }

Example: printing each element of an array is Θ(n). Now that's useful!

Most complexity functions that arise in practice are in Big-Theta of something. An example of a function that does isn't in Big-Theta of anything is λn. n²cos n.

Determining Asymptotic Complexity

Normally you can just look at a code fragment and immediately "see" that it is Θ(1), Θ(log n), Θ(n), Θ(n log n), or whatever. But when you can't tell by inspection, you can write code to count operations for given input sizes, obtaining T(n). Then you "guess" different values of f for which T ∈ Θ(f). To do this, generate values of T(n) / f(n) for lots of different f's and n's, looking for the f for which the ratio is nearly constant. Example:

package edu.lmu.cs.algorithms;

import java.util.Arrays;

/**
 * An application class that illustrates how to do an empirical
 * analysis for determining time complexity.
 */
public class PrimeTimer {

    /**
     * A method that computes all the primes up to n, and returns the
     * number of "primitive operations" performed by the algorithm.
     */
    public static long computePrimes(int n) {
        boolean[] sieve = new boolean[n];
        Arrays.fill(sieve, true);
        sieve[0] = sieve[1] = false;
        long ticks = 0;
        for (int i = 2; i * i < sieve.length; i++) {
            ticks++;
            if (sieve[i]) {
                ticks++;
                for (int j = i + i; j < sieve.length; j += i) {
                    ticks++;
                    sieve[j] = false;
                }
            }
        }
        return ticks;
    }

    /**
     * Runs the computePrimes() methods several times and displays the
     * ratio of the number of primitive operations to n, n*log2(log2(n)),
     * n*log2(n), and n*n, for each run.  The idea is that if the ratio is
     * nearly constant for any one of the expressions, that expression is
     * probably the asymptotic time complexity.
     */
    public static void main(String[] args) {
        System.out.println("        n         T(n)/n  T(n)/nloglogn"
                + "     T(n)/nlogn       T(n)/n^2");
        for (int n = 10000000; true; n += 5000000) {
            double time = (double)computePrimes(n);
            double log2n = Math.log(n) / Math.log(2.0);
            double log2log2n = Math.log(log2n) / Math.log(2.0);
            System.out.printf("%9d%15.6e%15.6e%15.6e%15.6e\n",
                    n, time / n, time / (n * log2log2n), time / (n * log2n),
                    time / ((double)n * n));
        }
    }
}

The output is

        n         T(n)/n  T(n)/nloglogn     T(n)/nlogn       T(n)/n^2
---------------------------------------------------------------------
 10000000   2.349563e+00   5.175961e-01   1.010413e-01   2.349563e-07
 11000000   2.355738e+00   5.179858e-01   1.007113e-01   2.141580e-07
 12000000   2.361341e+00   5.183378e-01   1.004120e-01   1.967784e-07
 13000000   2.366424e+00   5.186490e-01   1.001364e-01   1.820327e-07
 14000000   2.371590e+00   5.190404e-01   9.990302e-02   1.693993e-07
 15000000   2.375254e+00   5.191564e-01   9.963959e-02   1.583503e-07
 16000000   2.378816e+00   5.192966e-01   9.940077e-02   1.486760e-07
 17000000   2.382760e+00   5.195606e-01   9.920300e-02   1.401623e-07
 18000000   2.386342e+00   5.197811e-01   9.901218e-02   1.325745e-07
 19000000   2.389595e+00   5.199618e-01   9.882732e-02   1.257681e-07
 20000000   2.392305e+00   5.200526e-01   9.863752e-02   1.196152e-07
 21000000   2.394954e+00   5.201557e-01   9.846098e-02   1.140454e-07
 22000000   2.397970e+00   5.203615e-01   9.831373e-02   1.089986e-07
 23000000   2.400494e+00   5.204813e-01   9.815910e-02   1.043693e-07
 24000000   2.402350e+00   5.204755e-01   9.798898e-02   1.000979e-07
 .
 .
 .
 54000000   2.449024e+00   5.229676e-01   9.534299e-02   4.535229e-08
 55000000   2.449701e+00   5.229462e-01   9.527116e-02   4.454001e-08
 56000000   2.450639e+00   5.229837e-01   9.521139e-02   4.376141e-08
 57000000   2.452100e+00   5.231358e-01   9.517375e-02   4.301930e-08
 58000000   2.453286e+00   5.232321e-01   9.512714e-02   4.229804e-08
 59000000   2.454199e+00   5.232730e-01   9.507164e-02   4.159660e-08
 60000000   2.455236e+00   5.233429e-01   9.502255e-02   4.092060e-08
 61000000   2.455879e+00   5.233314e-01   9.495977e-02   4.026031e-08
 .
 .
 .

What we're seeing here is that the ratio T(n)/n is increasing, so the complexity is probably more than linear. The ratios T(n)/(n*log(n)) and T(n)/n² are decreasing so those functions are probably upper bounds. But T(n)/(n*log(log(n))) shows both some decreasing and increasing, and although we see an overall increase it's probably converging to some stable ratio for super huge n. It's a pretty good bet that the complexity ∈ Θ(n*log(log(n))), but we should really do a formal proof.

The Effects of Increasing Input Size

Suppressing leading constant factors hides implementation dependent details such as the speed of the computer which runs the algorithm. Still, you can some observations even without the constant factors,

The Effects of a Faster Computer

Getting a faster computer allows to solve larger problem sets in a fixed amount of time, but for exponential time algorithms the improvement is pitifully small.

More generally,

What if we had a computer so fast it could do ONE TRILLION operations per second?

As you can see, the gap between polynomial and exponential time is hugely significant. We can solve fairly large problem instances of high-order polynomial time algorithms on decent computers rather quickly, but for exponential time algorithms, we can network together thousands of the world's fastest supercomputers and still be unable to deal with problem set sizes of over a few dozen. So the following terms have been used to characterize problems:

Further Study

• Other functions for complexity measures: log log n, n^3/2, (log n)^k, n^{log n}, A(m,n), α(m,n), 2ⁿ/n, n²2ⁿ, ...
• Algorithms whose input size is quantified by more than one variable, as in graphs where n = the number of nodes and e = the number of edges and we find complexity measures such as Θ(e), Θ(n²), Θ(n log e), Θ(n²log e), ...
• Space Complexity

• Formalized complexity classes: DLOG, NLOG, P, NP, PSPACE
• Complexity measures for parallel, concurrent and distributed algorithms
• Pessimal algorithms and simplexity analysis
• The Complexity of Songs