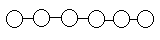Data Structures and Algorithms
Unit Goals
Importance
Welcome to the study of data structures and algorithms, a discipline within Computer Science.
A while ago, the ACM created a taxonomy of Computer Science, identifying eighteen knowledge areas. They are presented here for reference only—please don’t try to memorize this table! In the breakdown, Data Structures and Algorithms appears as a single, tiny topic:
| Knowledge Area | Code | Some Topics |
|---|---|---|
| Algorithms and Complexity | AL | Algorithmic Analysis • Algorithmic Strategies • Data Structures and Algorithms • Automata • Computability • Computational Complexity |
| Architecture and Organization | AR | Digital Logic and Digital Systems • Machine-level Data Representation • Assembly-Level Machine Organization • Memory System Organization and Architecture • Interfacing and Communication • Functional Organization • Multiprocessing and Alternative Architectures • Performance Enhancements |
| Computational Science | CN | Modeling and Simulation • Processing • Interactive Visualization • Data, Information and Knowledge • Numeric Analysis • Symbolic Computation • Mathematical Modeling • High-Performance Computing |
| Discrete Structures | DS | Logic • Sets, Relations, and Functions • Proof Techniques • Basics of Counting • Graphs and Trees • Discrete Probability |
| Graphics and Visualization | GV | Media Applications • Digitization • Color Models • Rendering • Modeling • Animation • Visualization |
| Human-Computer Interaction | HCI | Interactive Systems • Testing • Collaboration and Communication • Statistical Methods • Human Factors • Mixed, Augmented, and Virtual Reality |
| Information Assurance and Security | IAS | Defensive Programming • Threats and Attacks • Network Security • Cryptography • Web Security • Platform Security • Policy and Governance • Digital Forensics • Secure Software Engineering |
| Information Management | IM | Database Systems • Data Modeling • Indexing • Key-Value, Document, Relational, and Graph Databases • Query Languages • Transaction Processing • Distributed Databases • Physical Database Design • Data Mining • Information Storage and Retrieval • Multimedia Systems |
| Intelligent Systems | IS | Knowledge Representation and Reasoning • Search • Machine Learning • Reasoning Under Uncertainty • Agents • Natural Language Processing • Robotics • Speech Recognition and Synthesis • Perception and Computer Vision |
| Networking and Communication | NC | Networked Applications • Reliable Data Delivery • Routing and Forwarding • Local and Wide Area Networks • Resource Allocation • Mobility • Social Networking |
| Operating Systems | OS | Operating System Organization • Concurrency • Scheduling and Dispatch • Memory Management • Security and Protection • Virtual Machines • Device Management • File Systems • Realtime and Embedded Systems • Fault Tolerance • System Performance and Evaluation |
| Platform-Based Development | PBD | Web Platforms • Mobile Platforms • Industrial Platforms • Game Platforms |
| Parallel and Distributed Computing | PD | Parallel Decomposition • Communication and Coordination • Parallel Algorithms, Analysis, and Programming • Parallel Architecture • Parallel Performance • Distributed Systems • Cloud Computing • Formal Models and Semantics |
| Programming Languages | PL | Object Oriented Programming • Functional Programming • Event-Driven and Reactive Programming • Type Systems • Program Representation • Language Translation and Execution • Syntax Analysis • Semantic Analysis • Code Generation • Runtime Systems • Static Analysis • Concurrency and Parallelism • Type Systems • Formal Semantics • Language Pragmatics • Logic Programming |
| Software Development Fundamentals | SDF | Algorithms and Design • Fundamental Programming Concepts • Fundamental Data Structures • Development Methods |
| Software Engineering | SE | Software Processes • Project Management • Tools and Environments • Requirements Engineering • Software Design • Software Construction • Software Verification and Validation • Software Evolution • Software Reliability • Formal Methods |
| Systems Fundamentals | SF | Computational Paradigms • Cross-Layer Communications • State and State Machines • Parallelism • Evaluation • Resource Allocation and Scheduling • Proximity • Virtualization and Isolation • Reliability through Redundancy • Quantitative Evaluation |
| Social Issues and Professional Practice | SP | Social Context • Analytic Tools • Professional Ethics • Intellectual Property • Privacy and Civil Liberties • Professional Communication • Sustainability • History • Economics of Computing • Security Policies, Law, and Crime |
But don’t be fooled. Data Structures and Algorithms is not “just another topic.” It is one of the most central and important topics in all of Computer Science. Knowledge of data structures and algorithms is essential to gaining any sort of proficiency in nearly every one of the other topics in this table!
Why Must They Go Together?
In the table above, data structures and algorithms were mentioned together. Why?
- Computing systems are concerned with the storage and retrieval of information.
- For systems to be economical, the data must be organized (into data structures) in such a way as to support efficient manipulation (by algorithms).
- Choosing the wrong algorithms and data structures makes a program slow at best and unmaintainable and insecure at worst.
Expressed more powerfully:
Bob Barton, the main designer of the B5000 and a professor at Utah had said in one of his talks a few days earlier: "The basic principle of recursive design is to make the parts have the same power as the whole." For the first time I thought of the whole as the entire computer and wondered why anyone would want to divide it up into weaker things called data structures and procedures. Why not divide it up into little computers, as time sharing was starting to? But not in dozens. Why not thousands of them, each simulating a useful structure?
— Alan Kay, The Early History of Smalltalk
How Do They Go Together?
It’s very helpful to think of the data type as the bridge between data structures and algorithms.
Specific organizations or arrangements of data, whether sequential, hierarchical, arbitrarily linked up, hashed, specially indexed, or just thrown into unorganized buckets.
Recipes for carrying out computations. Algorithms are made up of a finite number of instructions woven together with control structures.
Data types combine data entities (units units of information) together with the algorithms that define the behaviors of these entities.
Data Types
So these data types are the key to everything right? What are they, exactly?
First of all, note that programs manipulate information, and information in a program is represented with entities. Entities are things like numbers, text, lists, and so on. To help us understand entities, it helps to classify them into types.
We have an intuition about what types are. As a first approximation, a type is just a set of values, for example:
- $\mathbb{N} = \{0, 1, 2, 3, 4, ...\}$
- $\mathbb{Z} = \{..., -2, -1, 0, 1, 2, ...\}$
- $\mathbb{B} = \{\textsf{false}, \textsf{true}\}$
- $\mathbb{R} = \textrm{the set of all real numbers}$
- $\mathbb{C} = \textrm{the set of complex numbers}$
- $\mathbb{H} = \textrm{the set of quaternions}$
- $\textsf{PrimaryColor} = \{\textsf{RED}, \textsf{GREEN}, \textsf{BLUE}\}$
- $\textsf{Suit} = \{\textsf{SPADES}, \textsf{HEARTS}, \textsf{DIAMONDS}, \textsf{CLUBS}\}$
- $\textsf{TwoDimensionalPoint} = \mathbb{R} \times \mathbb{R}$
- $\textsf{Card} = \{1..13\} \times \textsf{Suit}$
- $\textsf{Deck} = \textrm{the set of all permutations of Card}$
- $\textsf{SmallReal} = \{x \mid x \in \mathbb{R} \wedge 0.0 \leq x \wedge x \leq 1.0\}$
- $\textsf{Color} = \textsf{PrimaryColor} \rightarrow \textsf{SmallReal}$
- $\textsf{BTSMembers} = \{\textrm{Jin}, \textrm{Suga}, \textrm{J-Hope}, \textrm{RM}, \textrm{Jimin}, \textrm{V}, \textrm{Jungkook}\}$
- $\textsf{List<Integer>} = \mathbb{Z}^{*}$
- $\textsf{List<}\alpha\textsf{>} = \alpha^{*}$ (woah—that type is parametrized by a type variable)
- $\textsf{Tree<}\alpha\textsf{>} = \alpha \times \textsf{Tree<}\alpha\textsf{>}^{*}$ 🤯
That’s not really good enough, though! The reason why entities have certain types is that they behave in certain ways: you can multiply numbers, reverse lists, capitalize text, block users, revoke credentials, promote employees, and so on. Properly specifying a type requires defining how the entities of that type behave.
These behaviors are captured (algebraically 😮😮😮) as operations with zero or more inputs and a single output. For example:
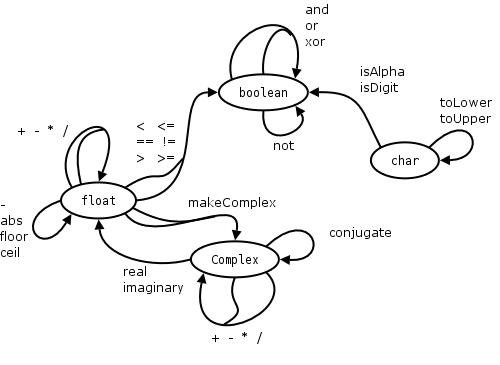
The same thing can be said without pictures, for example:
CLUBS: SuitHEARTS: SuitDIAMONDS: SuitSPADES: SuitACE: RankTWO: RankTHREE: RankFOUR: RankFIVE: RankSIX: RankSEVEN: RankEIGHT: RankNINE: RankTEN: RankJACK: RankQUEEN: RankKING: RankmakeCard : Suit × Rank → CardgetSuit : Card → SuitgetRank : Card → RanknewDeck : DeckpositionOf : Deck × Card → intcardAt : Deck × int → CardtopCard : Deck → Cardshuffle : Deck → Decksplit : Deck → DeckAh, now we have behaviors. A data type is a set of values together with operations that define their behavior.
Not every operation is applicable to every type. Types provide constraints on what we can and cannot say.
Draw a picture, and enumerate operations, for the type of integer lists. An integer list is a sequence of zero or more integers with operations such as obtaining the length, adding an item to a given position, removing the nth item, reversing, finding the position of a given item, etc.
Abstract Data TypesAs an aside: you will sometimes hear the term abstract data type, abbreviated “ADT.” People use this term to emphasize the fact that the “internal structure and internal workings of the operations” are somehow unknown to the outside world. Only the effects of the operations matter. To many people, though, saying “data type” is enough—all datatypes are “abstract” in that sense.
A useful exercise is to identify things in your world and try to list as many behaviors as you can. Here is a starter set:
| Data Type | Sample Behaviors |
|---|---|
| Number | negate • add • subtract • multiply • divide • remainder • modulo • to the power • mod_pow • to string • to string with a specific radix • negative infinity • positive infinity • $e$ • $\pi$ • floor • ceiling • round • truncate • $e$ to the power • natural log • log base 10 • log base 2 • hypot • sine • cosine • tangent • arc tangent • arc tangent given two values • square root • cube root |
| String | create from code points • create from UTF-8 bytes • get list of code points • get list of UTF-8 bytes • get ith code point or byte • get number of code points • get number of bytes • normalize • starts with • ends with • is this a substring? • index of • lower case • upper case • capitalize • slice • substring • split • join • trim • trim at start • trim at end • pad at start • pad at end • repeat • replace • append • interpolate • match |
| Boolean | true • false • and • or • xor • not • and-not • nand • nor |
| Point | x • y • distance to origin • distance to another point • midpoint between this point and another • quadrant • origin |
| Polygon | number of points • area • perimeter |
| List | create • destroy • add an element or elements • remove an element or elements • replace a single occurrence or multiple occurrence of an element • find (search for) an element or elements • get the size of (number of elements in) the collection • is it empty? • is it full? • enumerate the elements • filter (keep only certain) elements • merge lists together to form a new one • is this a sublist? • are these two lists equal? • make a copy of all or part of a list • serialize (convert to string or some other unique, recoverable representation) • deserialize (create from a serialized representation) |
| User | name • email • avatar • is logged in • log in • logout • block • assign roles • get timestamp the user was created |
| Player | name • id • score • update score • start turn • end turn |
| Timeline | label • list of posts • add post • delete post • update post • archive |
| TimelineItem | title • content • list of comments • add comment • remove comment • report comment |
Data Structures
A data structure is an arrangement of data for the purpose of being able to store and retrieve information. Usually a data structure exists in order to provide a physical representation of a data type.
For example, a list (a data type, which we saw above) can be represented by an array (a data structure) or by attaching a link from each element to its successor (another kind of data structure).
Wait, what are arrays and links?
Building Blocks
Data structures are built with three primary structuring mechanisms:
Objects
Groupings of properties into a single unit with named fields
Arrays
Collect multiple entities into positionally indexed, contiguous slots in memory
Links
Also known as references, allow arbitrary directional associations of entities
Let’s dive in. A object, also known as an record, struct, or named tuple, is a single entity that has many properties, where each property has a name and a value, which is another entity. Here is a simple object, can you guess what it represents?
An array is an entity that has a number of constituent elements, packed tightly together in memory and indexable by small natural numbers. In most programming languages, the first index is 0, in others (Julia, Lua, MATLAB), the first index is 1. Here are some cities in Alaska to visit (in order, because arrays are ordered):
Important: Note that were the properties of a object come together to make one conceptual thing; arrays are generally thought of as a collection of distinct things.
Objects and arrays can be nested inside each other. Here is a dog at the shelter that you should adopt:
And here is an array of objects, representing a polygon:
Theoretically, arrays and objects can do any thing, sort of, but not too conveniently. For example, here are two different people, and their pets:
Now here’s the question. Do these two people have the same pet, or are there two different dogs with the same name, the same birthday, the same breed, and the same everything else? It could be a coincidence, right? We would like a way to distinguish those two cases. That’s where links, also known as a references or pointers come in. The scenario in the previous picture shows two similar, but distinct, dogs, but the following picture shows the two people sharing a single pet:
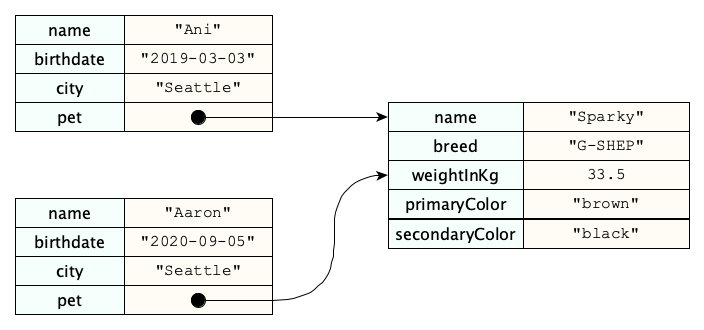
Links are helpful in so many other situations. Here’s an attempt to object information about a family using only objects. (For simplicity, we’re only showing some of the many fields we’d likely have irl.)
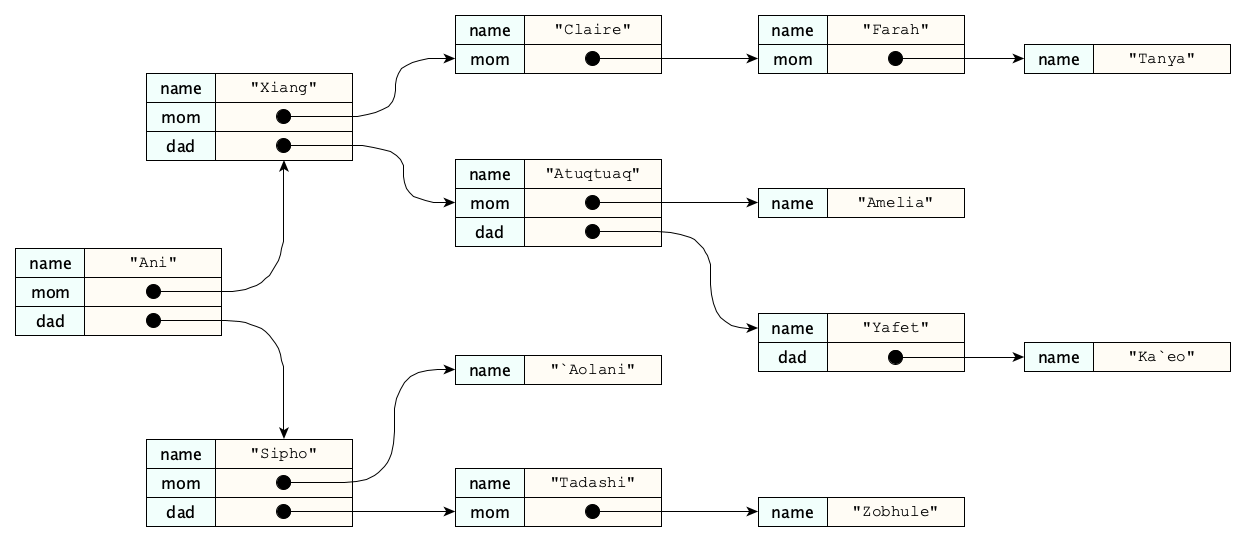
There is one huge problem with this scenario. If we wanted add properties like “spouse” or “guardian” or “best friend” then...ugh...try it. Really, try it. What if two different people were each others’ best friends?
We should have links here too, since after all, if two people have the same mom, the links are a great way to make clear they have the same mom rather than their separate moms have the same properties. Here’s the nested-object family tree above, using links to give each person their own identity:
You’ve probably noticed the various person entities above all have different numbers of properties. While this really isn’t a big deal from a modeling perspective, programs can (believe it or not) often run much more efficiently when similar objects all have exactly the same size. But to make things the same size, we’ll need a way to indicate that certain properties don’t reference anything. Such a reference is called a null reference. Here’s the family tree again, this time with null references:
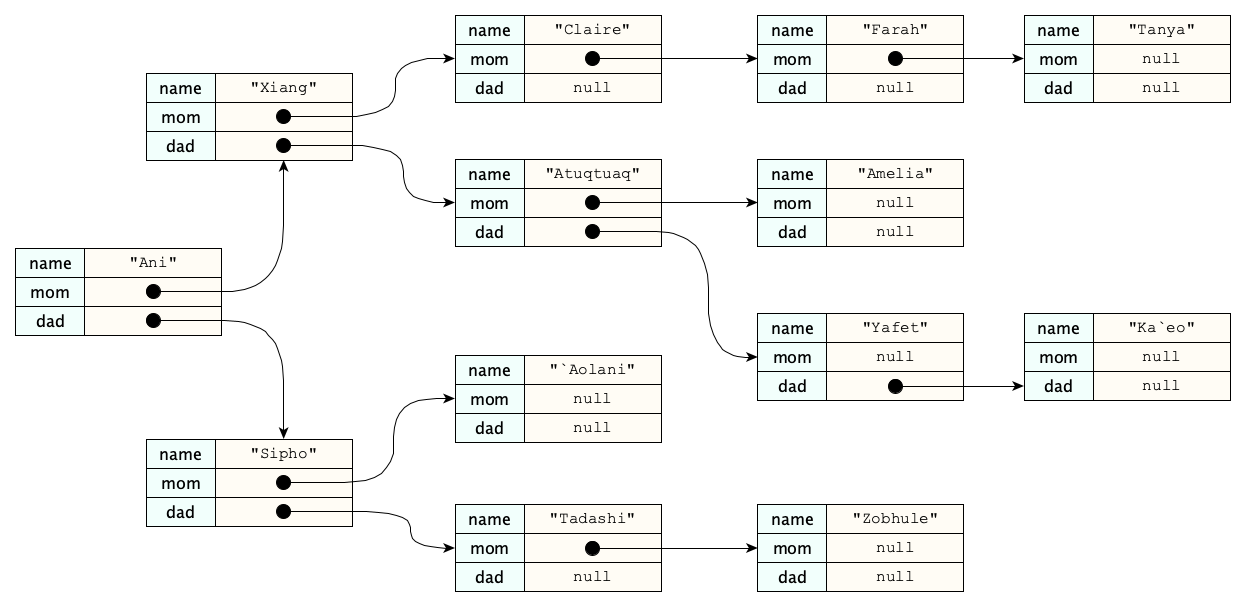
Null ReferencesWhat do you think of nulls? They seem powerful. They seem convenient. They are used practically everywhere. Most of the popular languages have them. But did you know, the null reference is a disaster known as the Billion Dollar Mistake? Watch its inventor, Sir Tony Hoare, take the blame for this abomination.
In many programming languages, not only must all similar objects have the same properties, but you are also not allowed to add new elements to an array and you are not allowed to add new properties to a object once the program is running. Hard to believe, but IT’S TRUE! In these languages the only way you can grow and shrink structures once a program is running is to use links. That’s why you might see structures like the following when you need variable-sized structures:
Arrangement of Elements
When building data structures, we must often think about the best ways to arrange the internal elements, as this impacts how we use the structure. Here are four classic arrangements that are good to know:
| Classification | Topology | Examples |
|---|---|---|
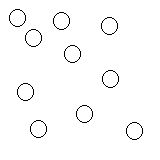
| SET (NON-POSITIONAL) | Unrelated
|
|
| SEQUENCE (LINEAR) | One-to-one
|
|
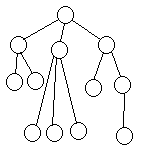
| TREE (HIERARCHICAL) | One-to-many
|
|
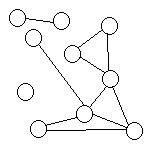
| GRAPH (NETWORK) | Many-to-many
|
|
These arrangements are actually rather conceptual, if you think about it, because one can still build them out of objects, arrays, and links in a variety of ways.
Choosing the Right Data Structure
Different data structures have different storage and performance characteristics. So when choosing a data structure, you should first figure out what kind of constraints you have. For example, in an accounting system, creation and deletion of a new account can be slow (they don’t happen too often), but lookup and update of balances happen all the time and must be extremely fast.
It turns out, in the study of data structures, people have found certain questions to pop up again and again and again and again. Being able to answer the following questions, and others like them, can make the difference between a system that satisfies its users and one that doesn’t.
- 🤔 Can the data structure be completely filled at the beginning and never change again, or will there be insertions intermingled with deletions, lookups, updates, and other operations?
- 🤔 Can items be deleted from the structure?
- 🤔 Does the order of insertion matter?
- 🤔 Do the elements of the structure need to be sortable?
- 🤔 Will the items always be processed in a well-defined order, or will random-access have to be supported?
Classic Data Structures
History is important. Over time, many data structures have become well-known (for various) reasons, and gaining knowledge of the classics is beneficial. Some of these are:- The Skip List
- The Cartesian Tree
- The Judy Array
- The a-b Tree
- The Red-Black Tree
- The Hash Table
- The Merkle Tree
- Wait, just kidding, there are HUNDREDS of these. I can’t make up a great list, but Wikipedia can. Check out Wikpedia’s List of Data Structures.
Algorithms
We design algorithms to carry out the desired behavior of a software system. Good programmers tend to use stepwise refinement when developing algorithms, and understand the tradeoffs between different algorithms for the same problem.
Classifying Algorithms
There are several classification schemes for algorithms:
- By problem domain: numeric, text processing (matching, compression, sequencing), cryptology, fair division, sorting, searching, computational geometry, networks (routing, connectivity, flow, span), computer vision, machine learning.
- By design strategy: divide and conquer, greedy, algebraic transformation, dynamic programming, linear programming, brute force (exhaustive search), backtracking, branch and bound, heuristic search, genetic algorithms, simulated annealing, particle swarm, Las Vegas, Monte Carlo, quantum algorithms.
- By complexity: constant, logarithmic, linear, linearithmic, quadratic, cubic, polynomial, exponential.
- Around the central data structures and their behavior, since in practice, your choice of data structure practically defines how the algorithms are going to work!
- By one of many implementation dimensions: sequential vs. parallel, recursive vs. iterative, deterministic vs. non-deterministic, exact vs. approximate, ....
Kinds of Problems
This classification has proved useful:
| Problem Type | Description |
|---|---|
| Decision | Given $f$ and $x$, is it true that $f(x)$? |
| Functional | Given $f$ and $x$, find $f(x)$ |
| Constraint | Given $f$ and $y$, find an $x$ such that $f(x)=y$ |
| Optimization | Given $f$, find the $x$ such that $f(x)$ is less than or equal to $f(y)$ for all $y$. |
Choosing the Right Algorithm
Being a computer scientist or software engineer is more than just studying algorithms that people have already written; one should be able to know when to apply which kind of algorithm for a given task, and even be able to come up with novel algorithms.
Choosing the right algorithm is both:
- an art 👩🏽🎨, because cleverness, insight, ingenuity, and dumb luck are often required to find efficient algorithms for certain problems
- a science 👩🏿🔬, because principles of algorithmic patterns and algorithm analysis have have been developed over time for you to use.
Classic Algorithms
History is important. Over time, many algorithms have become well-known for various reasons. Some of these are:- Euclid’s GCD
- The Fast Fourier Transform
- Miller-Rabin Primality Test
- Dijkstra’s Shortest Path
- Ford-Fulkerson Maximum Flow
- A* Search
- Wait, just kidding, there are HUNDREDS of these. I can’t make up a great list, but Wikipedia can. Check out Wikpedia’s List of Algorithms.
Summary
We’ve covered:
- Why data structures and algorithms are important
- Why they go together
- Data structures vs. algorithms vs. data types
- Data types = values + behavior
- The building blocks of data structures (the big three: objects, arrays, links)
- Four data structure topologies
- A super brief overview of the study of algorithms