An Introduction to Computation

What is Computation?

Information is that which informs.

Computation is the mechanical generation of new information from old information.

Computations are expressed within a programming language and carried out with automata.

The study of computation as a discipline is therefore the study of languages and automata.

The human understanding of, and application of, computing has evolved over millennia. It has arguably enhanced human capabilities. There is a history here that is empowering to know. History is an essential component of the study of any discipline. However:

[Computing is] complete pop culture. The big problem ... [is that] the electronic media we have is so much better suited for transmitting pop-culture content than it is for high-culture content. I consider jazz to be a developed part of high culture. [Jazz aficionados take deep pleasure in knowing the history of jazz, but] pop culture holds a disdain for history. Pop culture is all about identity and feeling like you're participating. It has nothing to do with cooperation, the past, or the future—it's living in the present. I think the same is true of most people who write code for money. They have no idea where [their culture came from]. —Alan Kay

Woah. He’s right. Let’s do something about this.

A Brief History

Here are some important events, people, works, and machines to be aware of in order to have a proper context for the study of computation.

In ancient times

Since antiquity, humans have been marking, matching, comparing, tallying, measuring, and reckoning.

A big step

Early inventories featured pictorial markings like 🌽🌽🌽🌽🌽 🍓🍓🍓. Then someone figured out they could save space by writing something like 5🌽 3🍓. An incredibly powerful idea: symbols representing quantities!

Numerals!

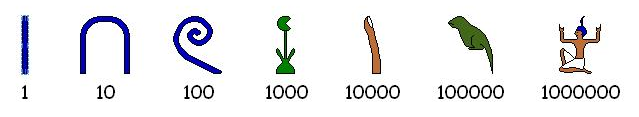
Early numeral systems like the Egyptian system were additive, but today positional systems are universal.

Recipes for calculation

Recipes, or lists of instructions, for manipulating quantities and measurements were sometimes recorded. Notable examples include:

• Babylonian Tablets 1800-1600 BC
• Rhind Mathematical Papyrus (~1550 BC)
• Euclid’s greatest common divisor method (~300 BC)
• Eratosthenes method for enumerating primes (~240 BC)
• Muḥammad ibn Mūsā al-Khwārizmī’s Al-Jabr (813-833), which included systematic solutions for linear and quadratic equations

Calculating machines

While humans could follow recipes and carry out reckoning with their fingers and toes, or use tally marks on bones, gains in efficiency and accuracy naturally arise with the creation of mechanical devices for calculation. Here are just a few examples:

• Abacus (earliest known from Sumeria 2700–2300 BC)
• Astrolabe (~200 BC)
• Antikythera mechanism (~200 BC)
• Slide Rule (1620s)
• Pascal’s calculators (1640s)
• Jacquard Loom (1804)
• Babbage’s Difference Engine (1820s) and Analytical Engine (1837)
• Hollerith’s Tabulating Machine (1880s)

The Analytical Engine was fascinating historically. Although never built, it was perhaps the world’s first programmable, general-purpose computer. Several programs are known to have been written for the device, the most famous of which—a program for the computation of Bernoulli numbers—was presented by Babbage’s collaborator Ada Lovelace in her translator’s notes to Luigi Menabrea’s article in Taylor’s Scientific Memoirs in 1843. (Also see this shorter summary). Lovelace is often considered the world’s first programmer. She is also widely admired as being perhaps the first to recognize the wide application of computing beyond arithmetic, writing that the Analytic Engine

might act upon other things besides number, were objects found whose mutual fundamental relations could be expressed by those of the abstract science of operations, and which should be also susceptible of adaptations to the action of the operating notation and mechanism of the engine.... Supposing, for instance, that the fundamental relations of pitched sounds in the science of harmony and of musical composition were susceptible of such expression and adaptations, the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent.

Philosophers, mathematicians, and logicians take interest

The 19th century saw wild advances in formal logic and the foundations of mathematics. Logic broke free of Aristotlean syllogisms. Cantor introduced us to the paradise of multiple infinities. Three philosophies about math even was emerged:

Major works of this era include:

• Boole’s Boolean Algebra (1847)
• Frege’s Begriffsschrift (1879)
• Peano’s Axioms (1889)
• Hilbert’s Program (early 1920s)
• Russell and Whitehead’s Principia Mathematica (1910–1913)

People learned that formalizing mathematics, or even giving it a logic foundation, was not so direct. Any attempt at providing a consistent, formal, axiomatic basis for mathematics (that included arithmetic) could never capture all truths. A shocking result at the time! Gödel proved this in 1931.

Computation gets formalized

Though Gödel showed there could be no logically consistent and complete formalization of all of mathematics, the question of whether there existed an effective, finite, decision procedure for all statements of mathematics remained open. (Yay, we’re back to computation!) This question is known as the Entscheidungsproblem. Hilbert thought such a procedure existed. Others did not. To prove him wrong, one needed to formalize the very idea of algorithm. The three main approaches of the 1930s were:

• Church’s Lambda Calculus
• The μ-recursive Functions (mostly worked out by Gödel, Kleene, and others)
• Turing Machines

Church and Turing both showed the Entscheidungsproblem had no solution. Poor Hilbert.

Story Time

We‘ll go over the story of Church, Gödel, and Turing in class only. You can’t find everything on the notes!

Turing

Turing’s paper is one of the most impactful and significant of all time.

• He gave a formalization of effective computation (algorithms) in a way people could all understand
• He gave evidence as to why his formalization, now called the Turing Machine, coincides with our intuitive notion of “computable” (the Church-Turing Thesis).
• He introduced computational universality: programs were just data (ok so far, not surprising) and, wait for it, a single machine could emulate, or “run,” any other machine (!!!!!!!!!!!!!!!!). Before this work, it was not known (but it may, we don’t know, have been suspected by some) that a truly universal computer could exist—separate machines were thought to be necessary for different tasks.
• He showed that some numbers were not computable, some functions were not computable, and that some questions could not be mechanically decided—and hence, that the Entscheidungsproblem had no solution.

We’ll study Turing’s paper, Turing machines, and the notion of universal computation in detail later in this course. Why? Turing is revered as the founder of computer science because of this work. The ideas that there are limits to computation, equivalent ways to express computation, and the existence of a truly universal computing machine make computer science a discipline. For now, watch this video:

Electronic computing machines

Turing's Universal Machine (1936) opened up a flood of new work in general purpose machines. Wikipedia’s History of Computing Hardware page covers both ancient devices and a fair number of machines from the 1930s–1960s. It is worth a look to see how we eventually got to the electronic devices that are ubiquitous today.

Programming Languages

von Neumann once angrily asked someone writing an assembler “Why would you ever want more than machine language?” Today that question sounds silly. Even assembly language is too low-level. One of the biggest proponents of high-level languages was Grace Hopper, who also happened to write the first compiler. Here are some notable high-level languages:

• Fortran, COBOL, LISP
• Algol, PL/1, Simula
• APL, J, K, Q
• CLU, Alphard, Euclid, Mesa, Cedar, Turing, Ada
• BCPL, B, C, C++, D, Rust, Zig, Odin, Swift
• Java, C#, Scala, Kotlin
• Perl, PHP, Hack, Tcl, Python, Ruby, Groovy, Lua
• Simula, Smalltalk, Object Pascal, Eiffel
• Concurrent Pascal, Occam, Linda, SR, Erlang, Elixir, Parasail, Chapel, Go
• Self, JavaScript, ActionScript, CoffeeScript, TypeScript
• Standard ML, CAML, Ocaml, F#, Elm, Reason
• Miranda, Haskell, PureScript, Idris
• Prolog, Mercury, Oz, Curry
• Agda, Coq, Lean
• Snobol, Icon
• Id, Val, Sisal
• SQL, Cypher, SPARQL
• Postscript
• MATLAB, R, Julia, Mojo
• Intercal, Unlambda, Brainfuck, Malbolge, Befunge, ZT, Java2K, LOLCODE
• GolfScript, Pyth, CJam, Jelly, 05AB1E, Stax

Language Implementation

Languages have to not only be expressive, but they have to be efficiently implementable. This is why we study compilers and interpreters. Two major parts of this field are:

• Linguistic Theories (from Chomsky and others) that enable parsing to be efficient
• Optimizations (Frances Allen was a major figure in this area)

Human-centric computing

People create programs for people. Areas with people-focus include:

• Graphics and user interfaces
• Computing in education
• Libraries for creative computing

Modern Trends

Trends in the modern computing era:

• Personal computers (1970s)
• Internet (1980s)
• Web (1990s)
• Mobile (2000s)
• Cloud (2010s)
• Generative AI (2020s)
• Quantum Computing (?)

Other Histories

Computing history is so much richer than the brief outline above. The following are highly recommended:

• Gabriel Robins’ remarkable A Brief History of Computing
• Wikipedia’s Computing History article
• Wikipedia’s Computing Timeline article
• Charles Petzold’s fabulous book The Annotated Turing

  

Beyond History

Computing is so much more than its technical core, its theoretical concepts, or even its history. Computing is a human activity. Computations, programming languages, and machines, are designed by humans for humans.

Grady Booch is building a remarkable transmedia documentary on the intersection of computing and the human experience.

The web version introduces itself as:

The story of computing is the story of humanity: this is a story of ambition, invention, creativity, vision, avarice, power, and serendipity, powered by a refusal to accept the limits of our bodies and our minds. Computing: The Human Experience is a transmedia project that explores the science of computing, examines the connections among computing, individuals, society, and nations, and by considering the history of computing contemplates the forces that will shape its future.

“powered by a refusal to accept the limits of our bodies and our minds”

It is worth immersing yourself in this content for hours.

Big Ideas

During humans’ creation of a science, art, and craft of computing, several major themes have emerged. They form the core of the field that we now call computer science. Among these themes, or big ideas, are:

• Symbols and symbol manipulation amplify our thought processes.
• The functions that can be computed comprise an infinitesimal fraction of the functions we know that exist.
• Theoretical computing devices (such as Turing Machines) are important for showing the limits of computation, but are not suitable for real computation.
• Universal computation is far, far from obvious, but we take it for granted today.
• Modern computers speed up time to such an extent that what we know and what we can know is qualitatively different than what we could know before computing.
• Programming languages enable the expression of computation at such a high level that creative and impactful computing become accessible to the masses.

Theories and Practices

In studying any discipline, humans create theories. A theory is an organized body of knowlege with explanatory and predictive powers. There are four major theories of computation:

• Language Theory, dealing with how computations are expressed
• Automata Theory, dealing with how computations are carried out
• Computability Theory, dealing with what is and is not computable
• Complexity Theory, dealing with how hard (in terms of resources like time and space) computations are

The practice of computing involves gaining proficiency in crafting computations (programs) in dozens of different programming languages and in many different programming styles, applying concepts, patterns, and idioms. It also includes the design and implementation of new programming languages and even new machines.

Designing one’s own language and implementing compilers and interpreters are essential activities in building a deeper understanding of computation.

Recall Practice

Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.

1. What is computation?
   The formal, mechanical, generation of new information from old information.
2. What is a programming language?
   A language for expressing computations.
3. What is an automaton?
   A machine for carrying out computations.
4. According to Alan Kay, why is computing history not widely known?
   Because pop culture, which computing arguably is, holds a disdain for history.
5. What is the significance of numerals?
   They allow large quantities to be expressed with fewer symbols.
6. Show how to represent the quantity twenty-one thousand two hundred thirty-seven using Egyptian Numerals:

   

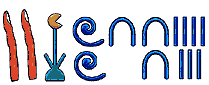
7. What are some ancient media on which early recipes for calculation were recorded?
   Babylonian Tablets and the Rhind Mathematical Papyrus.
8. What are some early famous nontrivial algorithms?
   Euclid’s greatest common divisor method and Eratosthenes method for enumerating primes
9. What were some of the accomplishments of Al-Khwārizmī?
   He wrote Al-Jabr, which included systematic solutions for linear and quadratic equations.
10. Where and when were abaci first known to be used?
    Sumeria 2700–2300 BC.
11. What could the Antikythera mechanism do?
    It was an analog computer that could predict astronomical positions and eclipses.
12. Babbage is known for designing to machines. Which ones?
    The Difference Engine and the Analytical Engine.
13. Was the analytical engine ever built?
    No.
14. What was Ada Lovelace’s published program in her famous Notes?
    A program for the computation of Bernoulli numbers.
15. What was Lovelace most known for besides the first published program?
    She was arguably the first to recognize and to write about the wide application of computing beyond arithmetic.
16. What did George Boole introduce to the world?
    Boolean Algebra.
17. What was Hilbert’s Program?
    A call to people of his time to formalize all of mathematics.
18. What did the logicists think math was? What did the formalists think it was? The intuitionists?
    Logicists: a branch of logic. Formalists: a game of manipulating symbols according to rules. Intuitionists: an invention for constructing objects and facts about them.
19. What was the Entscheidungsproblem?
    Hilbert’s question of whether there was an effective, finite, decision procedure for all statements of mathematics.
20. How did Church formalize the notion of effective computability?
    With the Lambda Calculus.
21. How did Turing formalize the notion of effective computability?
    With the Turing Machine.
22. What was Gödel's initial reaction to Church’s Lambda Calculus, and what did this reaction motivate Gödel to do?
    He was skeptical that the Lambda Calculus was a model for effective computability, so he created his own mode, the μ-recursive functions.
23. After Church demonstrated the equivalence of the Lambda Calculus and the μ-recursive functions, what was Gödel’s reaction?
    He thought his own model, the μ-recursive functions, must be insufficient.
24. When did Gödel finally accept the Lambda Calculus a model for effective computability?
    After Turing showed that the Lambda Calculus and Turing Machines were equivalent. All agreed that Turing machines were a sufficient model, thus the other two approaches must also be.
25. Name four stunning achievements of Turing’s famous paper.
    He gave a formalization of effective computation, showed that his formalization coincided with our intuitive notion of “computable”, introduced computational universality, and showed that some numbers (and by extension some functions) were not computable.
26. Why was the ENIAC famous?
    It was the first general-purpose electronic computer.
27. Who wrote the first compiler and what was it called?
    Grace Hopper. The A-0 System.
28. Why are programming languages important?
    They enable the expression of computation at such a high level that creative and impactful computing become accessible to the masses.
29. Why is LISP so loved?
    Simple syntax and semantics, homoiconicity, macros.
30. Why is Ruby so loved?
    It is extremely expressive, allows for rapid development, and has excellent metaprogramming facilities.
31. Why is CLU so significant?
    It introduced data abstraction, iterators, and exception handling.
32. What else is Barbara Liskov known for?
    She introduced the Liskov Substitution Principle.
33. What was Noam Chomsky’s biggest contribution to computer science?
    He introduced the Chomsky Hierarchy, which served as a foundation for modern parsing theory.
34. What is Frances Allen known for?
    She was a (if not the) major figure in the field of compiler optimization. It is said that among all the optimizations performed in modern compilers, she probably came up with or at least described 80% or more of the most important ones.
35. What year did Allen win the Turing Award?
    2006.
36. What even is Generative AI?
    AI that can create new things, like images, music, code, or text.
37. Where can I find more histories of computing?
    Gabriel Robins’ A Brief History of Computing, Wikipedia’s Computing History article, Wikipedia’s Computing Timeline article, and Charles Petzold’s The Annotated Turing.
38. What can I find at Computing: the Human Experience? (You should visit and explore the site to answer)
    Histories, timelines, stories, articles, films, interactive exhibits, and educational resources on computing and its impact on humanity (considering individuals, cultures, nations, and societies).
39. What are the four major theories of computation?
    Language Theory, Automata Theory, Computability Theory, and Complexity Theory.
40. Learning about computing requires a studying languages and automata. Why do we study these two subjects?
    Languages are for expressing computations, and automata are for carrying out computations.

Summary