Functional Programming

The Basics

What is it?

Functional programming is one of many recognized ways of programming, called paradigms. Roughly, the most common paradigms include:

• Imperative programming: programming with commands (Do this, then do that, etc.)
• Declarative programming: programming by saying what you want, not how it should be computed
• Structured programming: programming with nicely nested, crisp, control structures (no "gotos")
• Object oriented programming: programming around a society of objects, each with their own behaviors
• Logic programming: given a collection of facts and inference rules, an engine answers your questions
• Functional programming: programming by composing side-effect-free functions

There are many other paradigms as well, but those are the main ones.

What are some of FP’s characteristics?

In FP, we see that:

• Functions are first-class values: they can be assigned to variables and used pretty much as freely as numbers, booleans, and strings
• Functions do not have side-effects (e.g., no mutable variables, no I/O, no databases)
• Ubiquitous use of higher-order functions: functions that can (1) take functions as arguments and (2) return functions
• Recursion, folding, and powerful collection operators are used in place of loops
• Information hiding is handled through lexical closures (because there are no shared stateful objects)

Why is it important?

Three big reasons, at least. When you truly have no side effects, your code is automatically:

• Thread-safe, which is huge!
• Amenable to more compiler optimizations, especially in regard to core and thread allocation, and caching of previous results
• Easier to prove correct, because the result of calling a specific function with a specific argument is always the same no matter how many times you make that call. This is referential transparency.

But there's more!

• Functions as values give programmers more opportunities for reuse
• A lot of Big Data processing is based on the MapReduce paradigm which is straight out of functional programming theory.
• This style is more directly usable on multicore architectures (again, no shared state)

Like MPJ Videos? He has a whole series on Functional Programming as part of his Fun Fun Function channel:

Here is the entire playlist.

So what is Functional Programming?

Functional programming is programming by composing functions together.

Write lots of little side-effect-free functions that each do one thing and do it well. Compose these functions together using really cool combining forms.

Language Support

I think you can roughly group languages in a kind of spectrum like this:

Moving From Imperative to Functional

If your way of thinking is imperative, you view computation as a sequence of state-changing actions. The Turing Machine is pretty much the embodiment of this way of working. But Turing’s teacher, Alonzo Church, showed that computation could also be done by nothing more that composing functions, via his Lambda Calculus. In fact, the computing power of the Lambda Calculus and the Turing Machine have been proven to be exactly the same, and the Church-Turing Thesis shows that the TM and the λ-calculus are exactly what humans intuit as computing.

So if you have imperative code, where you are constantly updating state, how do you turn this in to functional code with function composition? Perhaps this is really just an art form, but there are three techniques that you’d employ:

1. Assignments become argument passing
2. Loops get done with recursion (generally tail recursion)
3. Mutable data structures become persistent data structures

Assignments → Argument Passing

This imperative code with mutable variables:

x = e
y = x + 5
y - 3

becomes (in JavaScript notation):

(y => y - 3)( (x => x + 5) e )

and in Elixir:

e |> &(&0 + 5) |> &(&0 - 3)

Loops → Tail Recursion

This standard for-loop:

let t = 10
while (t > 0) {
  console.log(t)
  t -= 1
}
console.log('LIFTOFF')

can be done like this:

(function countDown(t) {
  if (t === 0) {
    console.log('LIFTOFF')
  } else {
    console.log(t)
    countDown(t - 1)
  }
})(10)

Make sure the recursion is the last thing you do, otherwise the calls will pile up on the stack and that wastes memory big time! For example this code is AWFUL:

function factorial(n) {
  return n <= 0 ? 1 : n * factorial(n-1)
}

It is awful because it works like this:

factorial(4)
  = 4 * factorial(3)
  = 4 * (3 * factorial(2))
  = 4 * (3 * (2 * factorial(1)))
  = 4 * (3 * (2 * (1 * factorial(0))))
  = 4 * (3 * (2 * (1 * 1)))
  = 4 * (3 * (2 * 1))
  = 4 * (3 * 2)
  = 4 * 6
  = 24

but this code is much better:

function factorial(n) {
  function f(n, a) {
      return n <= 0 ? a : f(n-1, n*a)
  }
  return f(n, 1)
}

The better code is called tail recursion. It works like this:

factorial(4)
  = f(4, 1)
  = f(3, 4)
  = f(2, 12)
  = f(1, 24)
  = 24

No accumulation on the stack! In fact a good compiler will actually optimize away the recursive call and turn it into a jump to the start of the function (with the new parameters of course). So tail recursion is just as efficient as loops.

In general though, there are often so many operators on arrays (or streams or sequences) that you don’t even need to write the recursion yourself. You remember map, filter, reduce, every, some, takeWhile, dropWhile, flatMap, and friends, right?

Mutable Data Structures → Persistent Data Structures

If you can’t have shared mutable state, how do you add to a list? Insert into a tree? Remove an element from a set? Replace a value in a dictionary?

You don’t have to! Add, delete, and update operations return a new data structure! So:

• Adding to a data structure returns a new structure (with certain elements copied if needed)
• Removing from a data structure returns a new structure (with certain elements copied if needed)
• Updating in a data structure returns a new structure (with certain elements copied if needed)
• Reversing a list returns a new list (with probably all the elements copied)

If we return a new structure, the old one still hangs around; we have what are called persistent data structures. But is it efficient to keep the old ones around? What do you think happens here?

let
    a = replicate 50 "dog"
    b = "cat" : a
in
    print (a, b)

Do you think we copy all the nodes of list a? Actually no, the (:) operator is efficient. This happens:

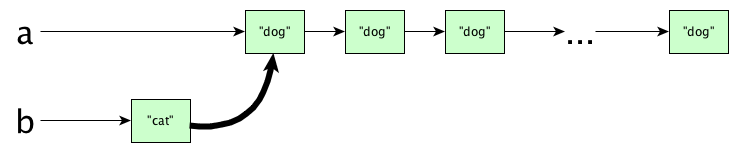
But, but, aren’t a and b sharing internal data? What would happen if we mutate a? Wouldn’t b get mutated too? Isn’t this bad?

ANSWER: Calm down, you cannot mutate data structures. Since they are immutable, this sharing is quite alright.

You do need to be aware of these inner workings, because efficiency matters. Consing to the front of a list is fine, but appending is a totally different story: if we had written b = a ++ ["cat"] then we would (in general) need an expensive copy.

Case Study

Let's implement the famous greedy change making algorithm for U.S. quarters, dimes, nickels, and pennies, several ways. The idea is that a single value is input and the result is an array of the form [q,d,n,p].

Step 1: A non-functional solution, using mutable variables

Let’s start with the painfully traditional, step-by-step, mutable variable approach, that builds up an array in a for-loop. First, JavaScript:

function change(amount) {
  let result = [];
  let remaining = amount;
  for (let value of [25, 10, 5, 1]) {
    result.push(Math.floor(remaining / value));
    remaining %= value;
  }
  return result;
}

In Python:

def change(amount):
    result = []
    remaining = amount
    for value in [25, 10, 5, 1]:
        result.append(remaining // value)
        remaining %= value
    return result

In Ruby:

def change(amount)
  result = []
  remaining = amount
  [25, 10, 5, 1].each do |value|
    result << remaining / value
    remaining %= value
  end
  result
end

In Java:

public static List<Integer> change(int amount) {
    var result = new ArrayList<Integer>();
    int remaining = amount;
    for (var value : List.of(25, 10, 5, 1)) {
        result.add(remaining / value);
        remaining %= value;
    }
    return result;
}

Let's try to understand how this works:

Iteration  value  remaining   result
---------------------------------------
        0     25         99   []
        1     10         24   [3]
        2      5          4   [3,2]
        3      1          4   [3,2,0]
        4                 0   [3,2,0,1]

Solution 2: A functional (no-variables) solution—recursion, not loops

We can make a slight change to the previous table:

values    remaining   result_so_far
-----------------------------------
[25,10,5,1]      99   []
[10,5,1]         24   [3]
[5,1]             4   [3,2]
[1]               4   [3,2,0]
[]                0   [3,2,0,1]

Now, let’s make a function c(values,remaining,result) whose input is a row of the table and whose output is the call for the next row of the table. Ooooooh. And, of course, when values is empty, it’ll output the result. Like this:

c([25,10,5,1], 99, [])
    = c([10,5,1], 24, [3])
    = c([5,1], 4, [3,2])
    = c([1], 4, [3,2,0])
    = c([], 0, [3,2,0,1])
    = [3,2,0,1]

The second and third lines say: "Changing 24 cents with dimes, nickels, and pennies, given that you have three quarters already, is done by changing 4 cents with nickels and pennies, given that you already have three quarters and two dimes."

In JavaScript:

function change(amount) {
  function c(values, remaining, result) {
    if (values.length === 0) {
      return result;
    } else {
      return c(values.slice(1), remaining % values[0], [...result, Math.floor(remaining / values[0])]);
    }
  }
  return c([25, 10, 5, 1], amount, []);
}

This is probably a terrible solution in JavaScript. JavaScript arrays are mutable, so this code likely makes copies whenever the new arrays were passed along. This is horribly inefficient, but suppose the compiler could figure out that we never actually change the array of denominations, and manages to shares state (without copying) among each of the parameters. In some languages, lists or arrays are defined to be immutable, so this sharing behavior is essentially wired into the language definition, so this kind of code is fast. This happens in Elm:

change amount =
  let c values remaining result =
    case values of
      [] -> result
      value::rest ->
        c rest (remaining % value) (result ++ [remaining // value])
  in
    c [25,10,5,1] amount []

and in Standard ML:

fun change amount =
  let
    fun c [] remaining result = result
      | c (value::rest) remaining result =
          c rest (remaining mod value) (result @ [remaining div value])
  in
    c [25,10,5,1] amount []
  end;

Solution 3: A solution using reduce

Reduction is cool. Look how we flow the partial results through the array of denominations:

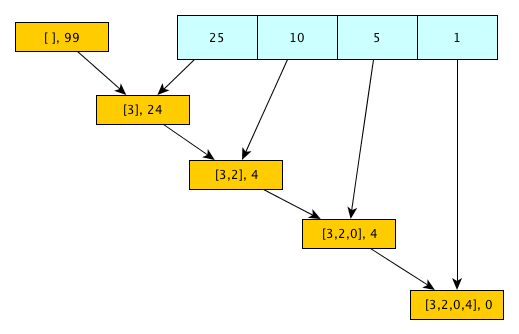
Our code gets concise but I’m not sure if it’s any more readable:

function change(amount) {
  const c = (acc, value) => [acc[0].concat([Math.floor(acc[1]/value)]), acc[1]%value];
  return [25, 10, 5, 1].reduce(c, [[], amount])[0];
}

How about the Clojure version?

(defn change [amount]
  (reduce (fn [accumulation value]
    (let [left (peek accumulation)]
      (conj (pop accumulation) (quot left value) (rem left value))))
    [amount]
    [25 10 5]))

Higher Order Functions

A higher order function is a function that can be passed functions as arguments or that returns a function. The simplest examples are probably:

function twice(f, x) {
  return f(f(x))
}

function apply(f, x) {
  return f(x)
}

function compose(g, f) {
  return x => g(f(x));
}

It is very common to see higher-order functions that operate on collections. This often makes your code much simpler since you don't need loops and conditionals! Examples:

• forEach
• every (all)
• some (any)
• one
• map
• reduce (inject, fold)
• reduceRight (injectRight, foldRight)
• mapConcat (flatmap)
• takeWhile
• dropWhile
• find (keep, select)
• findAll (filter, keepAll, selectAll)
• reject
• partition

It is also common to see a sort function that is higher-order; you pass in the comparator function.

Closures

Closures can be used to hide state and do interesting things like make generators. When an inner function is sent outside its enclosing function, it is called a closure. Here outer variables that live in a wrapping scope are retained. Simple example:

const nextFib = (() => {
  let [a, b] = [0, 1]
  return () => {
    [a, b] = [b, a + b]
    return a
  }
})()

nextFib()    // 1
nextFib()    // 1
nextFib()    // 2
nextFib()    // 3
nextFib()    // 5
nextFib()    // 8

Fun fact: the expression that we assigned to nextFib is called an IIFE (an acronym for immediately invoked function expression). Do you see why it is called that?

A couple caveats with closures:

• You don’t always need them. Modern languages like JavaScript have lots of other devices and features, e.g. actual generators, that are often used instead of closures for hiding state.
• Be aware of an interesting kind of JavaScript Memory Leak

Purity and Side Effects

So, can we really program entirely with pure functions? Wait, pure functions? What are those again? Kris Jenkins explains it better than I can, so read Kris’s article now. Also read part two.

Hopefully you read the article(s). The TL;DR is that a pure function is one in which all implicit contextual inputs (side causes) become official arguments to a function, and any implicit outputs (side effects) become part of the official function return value. Something like:

    f (arg, context) = (result, newContext)

Roughly speaking, if context contained a file stream, and f read from it, then the return result would be whatever the function did with the head of the stream, and the returned context would be the tail of the stream.

In practice, we can represent this context by wrappers around values, Optional types are great examples of this! Haskell does IO in much the same way: IO values wrap the data read from and written to streams. And IO objects are Monads. Here are some basic functions:

    getLine :: IO String
    putStrLn :: String -> IO ()
    print :: Show a => a -> IO ()

We can play with this in the REPL. If you use getLine in the REPL, you’ll have to type something in and hit Enter, of course.

Prelude> getLine >>= (putStrLn . ("You said " ++))
Hello world
You said Hello world
Prelude> print 1 >> print 2 >> print 3
1
2
3

Yes, these wrappers (whether for optionals, lists, I/O streams, and so on) are monads. Read about monads at Wikipedia if you need a refresher.

Theoretical Foundations

The idea of functional programming is rooted in (1) the ideal of the mathematical function, and (2) the theory of combinators so let's take a quick review of these things.

Functions

Informally, a function (in mathematics) is a mapping from an argument to a result. It always produces the same result for the same argument. More formally, in set theory, a function from a set A to a set B is a subset of A × B such that each element of A appears exactly once as the first component of a tuple in the set.

Functions in most programming languages have side-effects, so don’t confuse a programming language function with a mathematical function. The PL term for a mathematical function is, you’ll recall, a pure function.

See Wikipedia for more.

The Lambda Calculus

See Wikipedia's article for a nice introduction. If you like my notes, I have a page, too.

Combinators and Combinatory Logic

See Wikipedia.

Academic-sounding terms, tho

When you start to get theoretical, you’ll likely run into some fancy-sounding terms. The theoretical foundations of FP seem to have a few. You don’t need to know these terms, unless perhaps you get challenged by some know-it-all and you want to put them in their place. Well, here are the big three—functor, monoid, monad:

Functor

A functor is a generic object you can “map” over. Hey, arrays have a map method! Are arrays functors? HECK YEAH!! But theoretically, at least, what exactly is a “map”? A map function is any operation on the functor that:

• Transforms each element of the functor
• Returns a new functor that has the same shape as the original functor

Think of a functor as an object of a wrapped type F[T] and the map function has type (T→U)→F<T>→F<U>: It applies a function of type T→U to each element of a collection of Ts to get a collection of Us.

A JavaScript array is a functor because Array.prototype.map (1) takes in a transformation function that operates on (transforms) the elements, (2) returns a new array that has the same size as the original array.

Functors are cool because they allow for composition in a neat way: map calls can be chained.

Monoid

A monoid is something with a binary associative operator and an identity for that operator. A list is a monoid because it has an append operation with the empty list as the identity for that operation.

Also integers with addition (identity = 0) and multiplication (identity = 1). And strings with concatenation (identity = empty string). Floating point numbers with a max operation (identity = positive infinity). There are more examples, but this gets you started.

Why are they cool? They can be folded! In any order, due to associativity. 🙂

Monad

A monad is something with a constructor and a flatMap operation. In slightly more detail, a monad is an instance of a wrapper type (the monad type). The monad type M<T> wraps objects of some base type T, and contains two functions:

• A constructor function that wraps a value. The constructor has type T → M<T>
• A flatmap function that takes a function of type T → M<U> and a value of type M<T> that unwraps the value then applies flatmap to the unwrapped value.

Why are they interesting? Because monadic applications can be chained! They make really cool pipeline-esque code.

More examples of monads:

TODO

Functional vs. Object-Oriented

A parting shot: you may think that functional and object-oriented programming are diametrically opposed. Object-oriented programming is all about state, right? And functional programming is all about avoiding state, right?

Not really. Both, if done well, want to encapsulate state!

• In OOP, we hide state inside objects, and objects communicate only by sending messages.
• In FP, we hide state inside functions, and functions communicate by calling each other.

Where they differ, is perhaps, that OOP tends to be okay with mutability. Send a message to an object and it may change its internal state then respond. Every time you message an object with one of these mutable “methods” the responses and effects may be different. Functional programming tends to avoid this. You do need effects, of course, but in FP, you isolate this as much as possible. Sometimes in clunky ways, sometimes elegantly. For instance, Standard ML will say “here are mutable references” and Haskell says “hmm let’s get this into an IO Monad and just expose it in main.”

Bottom line: Whatever style you use, write as much code as you can with immutability in mind. When you need side-effects or impure operations (current time, random numbers, databases), fine. Make the interfaces to these parts of the system clear. That is, if you can....

Point-Free Programming

So moving from imperative programming to pure functional programming gets rid of assignments. The only “variables” in your program are function parameters. There aren’t even any local variables: those bindings in let expressions are actually function parameters:

TODO Example

But guess what? We can go one step further and even eliminate parameters! Every value is either an atom (or other primitive like a number, boolean, or string) or a function. Some functions operate on functions and are sometimes called functionals. When you program this way you are doing point-free programming, also known as tacit programming. In some sense, these styles are a very extreme kind of functional programming. If a language were to be entirely a tacit language you might not like it, but very often the ideas from tacit programming can make your every day programming better!

TODO - lots more to say here

Wikipedia has more on tacit programming and the related notion of function-level programming.

Summary