Graph Algorithms
Connected Components
Euler Trails and Tours
Topological Sorting
Minimum Spanning Tree
Shortest Paths
Max Flow
Vertex Cover
Traveling Salesperson Problem
Hamilton Paths and Cycles
Traversals
A traversal is a visting of each node in a graph in some particular order, generally based on moving along edges. We’ll use this example graph, and head out from node A:
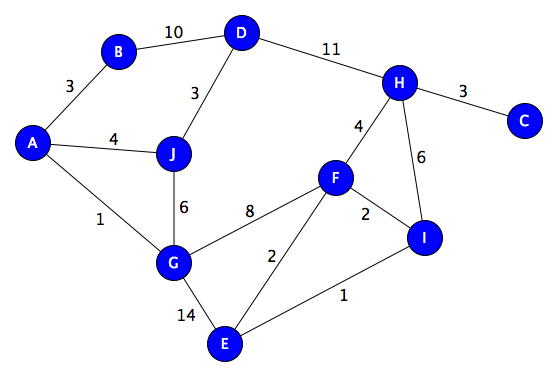
Breadth-First
Works level-by-level. Finds shortest path by number of hops. Implement with a queue:
A -- enqueue the start node A
B J G -- choose (dequeue) A, enqueue its neighbors B, J, G
J G D -- choose B, enqueue D
G D -- choose J, no untouched neighbors
D F E -- choose G, enqueue F and E
F E H -- choose D, enqueue H
E H I -- choose F, enqueue I
H I -- choose E, nothing to enqueue
I C -- choose H, enqueue C
C -- choose I, no untouched neighbors
-- choose C, nothing to enqueue, queue is empty, we're done!
def breadth_first(self, start):
q = [start]
visited = {start}
while not q.empty():
n = q.dequeue()
yield n
for e in n.outgoing_edges:
o = e.other_end_of(n)
if o not in visited:
visited.add(o)
q.enqueue(o)
Depth-First
Keep going and backtrack when needed. Use a stack or recurse.
A -> J -> D -> B (woops, stuck, backtrack to D) -> H -> F -> E -> G (backtrack to E) -> I (backtrack to E, then F, then H) -> C
def depth_first(self, start)
visited = {}
def dft(n):
visited.add(n)
yield n
for e in n.outgoing_edges
o = e.other_end_of(n)
if o not in visited:
dft(o)
dft(start)
Traditionally when we do this on directed graphs, we mark each edge as a discovery (tree) edge, back edge, forward edge or cross edge. Details at Wikipedia.
Connected Components
To determine is a graph is connected, run a traversal (breadth-first or depth-first) from any node and see if every node gets covered.
To determine the blocks (connected components), keep running traversals until all the nodes are exhausted.
Euler Trails and Tours
Can you find a way to cross each bridge exactly once and end up where you started?
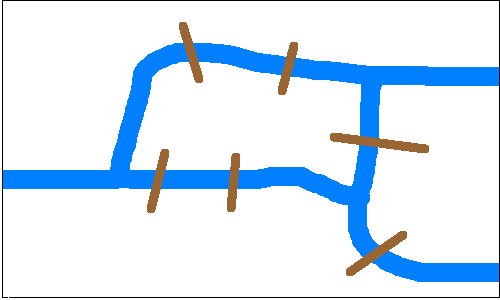
Euler proved that you can’t. The corresponding graph has an Euler Trail but no Euler Tour. Here's the theorem:
A connected graph has an Euler Tour iff the number of nodes with odd degree is zero, and has an Euler Trail iff the number of nodes with odd degree is two.
def has_euler_tour(self):
return all(even(n.degree) for n in self.nodes)
def has_euler_trail(self):
return sum(1 for n in self.nodes if odd(n.degree)) == 2
def has_euler_trail_or_euler_tour(self):
return sum(1 for n in self.nodes if odd(n.degree)) in (0, 2)
Topological Sorting
A topological sort of a directed graph is an ordering $S$ on the nodes such that whenever an edge $(v_1,v_2)$ appears in $G$ then $v_1$ comes before $v_2$ in $S$.
This shows up a lot: it tells us what order to do things in (task scheduling). Examples:
- Compilers need to order certain instructions.
- Factory machines need to order certain assemblies.
- Spreadsheets have to respect certain evaluation orderings.
- Modules might have to be included in some order.
- Programs might need to be compiled or linked in some order.
- Drawings may have layers that need to be respected.
The Naive Algorithm
output = []
while not g.empty:
n = g.some_node_with_no_incoming_edges
if not n:
raise Error('Graph has no topological sort')
output.append(n)
g.remove_node_and_all_incident_edges(n)
return output
That's destructive!
Another Algorithm
output = []
marks = {}
while len(marks) != g.node_count:
n = an_arbitrary_unmarked_node()
visit(n)
return output
def visit(n):
if marks[n] = 'pending':
raise Error, 'graph has a cycle'
if n not in marks:
marks[n] = 'pending'
for each o in n.outgoing:
visit(o)
marks[n] = 'complete'
output.prepend(n)
Minimum Spanning Tree
A spanning tree of graph $G$ is a subgraph of $G$ that is a tree and contains every node of $G$. A minimum spanning tree is a spanning tree with the minimum weight over all the edges.
These algorithms assume the graph is connected.
Prim's Algorithm
def mst(self):
t = Graph()
t.add_node(self.random_node())
while t.node_count < g.node_count:
n, e = closest_node_not_already_in(t)
t.add_node_with_edge(n, e)
return t
Getting the closest node not already in the tree can be managed by a priority queue.
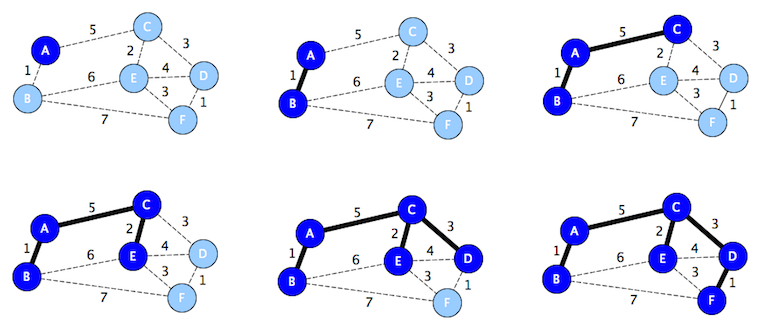
Kruskal's Algorithm
def mst(self):
t = Graph()
for e in sorted_by_edge_weight(g.edges):
n1, n2 = e.endpoints
if not (n1 in t.nodes and n2 in t.nodes):
t.add_edge(e)
return t
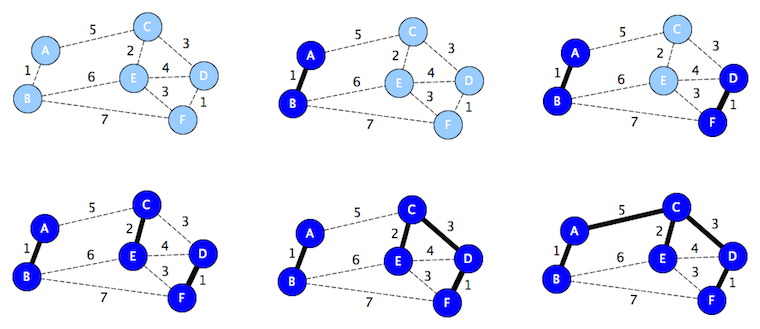
This can be sped up with a check that the last edge has been added.
Shortest Paths
Finding the “shortest” is really a family of problems. Do you want:
- The shortest path from one node to another (single-pair)?
- The shortest paths from one node to all others (single-source)?
- The shortest paths from all nodes to one node (single-destination)?
- The shortest paths between every pair of nodes (all-pairs)?
And your choice of algorithm might depend on whether:
- Are negative edge weights allowed?
- Are negative cycles allowed?
Before we go on, convince yourself that even for graphs with all positive weights, the pure greedy solution to even the single-pair shortest path does not work. Why doesn't it?
Dijkstra's Algorithm
For: single-source, no negative edges. Implement with a priority queue.

Starting with A:
(A,0) (B,3) (J,4) (G,1) (B,3) (J,4) (F,9) (E,15) (J,4) (F,9) (E,15) (D,13) (F,9) (E,15)(D,13)(D,7) (F,9) (E,15) (H,18)(E,15)(H,18)(E,11) (I,11) (H,13) (I,11) (H,13) (H,13) (C,16)
If you want to keep track of the paths themselves, remember the predecessor:
(A,0,None) A (0) (B,3,A) (J,4,A) (G,1,A) A-G (1) (B,3,A) (J,4,A) (F,9,G) (E,15,G) A-B (3) (J,4,A) (F,9,G) (E,15,G) (D,13,B) A-J (4) (F,9,G) (E,15,G)(D,13,B)(D,7,J) A-J-D (7) (F,9,G) (E,15,G) (H,18,D) A-G-F (9)(E,15,G)(H,18,D)(E,11,F) (I,11,F) (H,13,F) A-G-F-E (11) (I,11,F) (H,13,F) A-G-F-I (11) (H,13,F) A-G-F-H (13) (C,16,H) A-G-F-H-C (16)
A*
Finds the shortest distance from a start node to some goal node. Here distances are “costs”.
TODO
Bellman-Ford
For: single-source, negative edges allowed. Extends Dijkstra's algorithm by relaxing the distance to every node at each step.
def shortest_paths(self, start):
distance, pred = {}, {}
for n in g.nodes:
dist[n] = 0 if n is start else infinity
predecessor[start] = None
# Relax |V|-1 times
for i in range(1, g.node_count):
for e in g.edges as (u,v):
if distance[u] + e.weight < distance[v]:
distance[v] = distance[u] + e.weight
predecessor[v] = u
# If we can relax more there MUST have been a negative cycle
for e in g.edges as (u,v):
if distance[u] + e.weight < distance[v]:
raise Error, 'Negative cycle detected'
return distance, predecessor
Max Flow - Min Cut
...
Vertex Cover
...
Independent Set
...
Traveling Salesperson
...
Hamiltonian Paths and Cycles
...