Information

Symbols and Alphabets
A piece of (human-usable) information can be represented as a string of symbols; some examples are:
91442.3e-4Stay behind the yellow line!/Pecs/Los Angeles/Berlin/Madrid//1 2/3 0/2 2/2 0/3 2///(* (+ 4 3) (- 9 7))int average(int x, int y) {return (x + y) / 2;}<dog id="30024"><name>Lisichka</name><age>13</age></dog>{"type": "dog", "id": "30024", "name": "Lisichka", "age": 13}∀α β. α⊥β ⇔ (α•β = 0)1. f3 e5 2. g4 ♛h4++
The symbols that make up pieces of data are chosen from some finite alphabet, such as $\{0,1,2,3,4,5,6,7,8,9\}$ for the language of natural numbers, or $\{0,1,2,3,4,5,6,7,8,9,\textrm{e},\textrm{E},+,-\}$ for the language of floating-point numbers. In reality, the alphabet you choose is irrelevant because it is always possible to recode any alphabet into a two-symbol alphabet. For example, let’s say you have an alphabet $\{a,b,c,d,e\}$. You can recode this into the alphabet $\{0,1\}$ as follows:
| $a \rightarrow 000$ |
| $b \rightarrow 001$ |
| $c \rightarrow 010$ |
| $d \rightarrow 011$ |
| $e \rightarrow 100$ |
Then the word $cab$ becomes $010000001$ in the new alphabet.
Encoding
In fact, all information, whether it be numbers, characters, programming instructions, pictures, or complex data of any kind, can be encoded in strings from $\{0,1\}$, which we call bit strings. (The term bit is short for binary digit.)
Often for ease of presentation we look at the bit strings in chunks of eight bits; these units are called octets, which is a more correct term than byte.
Also, bit strings can get very long, so we sometimes compress them by naming chunks of 4 bits as follows: $0000 \rightarrow 0$, $0001 \rightarrow 1$, $0010 \rightarrow 2$, $0011 \rightarrow 3$, ... $1001 \rightarrow 9$, $1010 \rightarrow A$, $1011 \rightarrow B$, $1100 \rightarrow C$, $1101 \rightarrow D$, $1110 \rightarrow E$, and $1111 \rightarrow F$. That way, instead of writing
10000111110001000100111110101001
you can just write
87C44FA9
Interpretations
Since everything can be encoded into bit strings, decoding a bit string into the thing it encodes depends on its interpretation. For example, the bit string 1101010010110010 has the following meanings (you don’t have to know what these interpretations are, you just need to appreciate that different interpretations exist):
| Interpretation | Meaning |
|---|---|
| Unsigned Short Integer | 54450 |
| Signed Short Integer | -11086 |
| UTF-16 String | The character HANGUL SYLLABLE PHIEUPH WE SSANGKIYEOK: 풲 |
| UTF-8 String | The character ARMENIAN CAPITAL LETTER BEN: Բ |
| ISO 8859-1 String | The two-character string LATIN CAPITAL LETTER O WITH CIRCUMFLEX followed by SUPERSCRIPT TWO: Ô² |
| IA-32 Machine Instruction | An instruction that will divide the value in the AL register by 178, placing the quotient in the AH register and leaving the remainder in AL |
Functions
Information Processing is the transformation of one piece of data into another; the mathematical abstraction of this transformation is called a function. You probably already have a sense of functions. Consider:
double, which takes a number and returns twice that numberplus, which takes a pair of numbers and returns their sumnextMove, which takes a state of a game and returns the next (best?) move that should be madeupperCase, which takes a piece of text and returns a string like it but with all letters capitalizedsorted, which takes a list of things and returns a new list containing the same values in sorted ordereven, which takes a number and returns true or false depending on whether the number is eventint, which takes an image, a color value, and a number, and tints the image with the given color by the given amounttwice, which takes a function and a value and applies the function to the result of applying the function to the value
An infinite number of functions exist. Note to mathematicians: there exists an uncountably infinite number of possible functions.
Functions are applied to arguments to produce their results. For example:
double(3.5) ⇒ 7plus(4, -3) ⇒ 1upperCase("Please don’t shout!") ⇒ "PLEASE DON’T SHOUT!"sorted([4, 7, 1]) ⇒ [1, 4, 7]even(797) ⇒ falsetwice(double, 5) ⇒ double(double(5)) ⇒ double(10) ⇒ 20
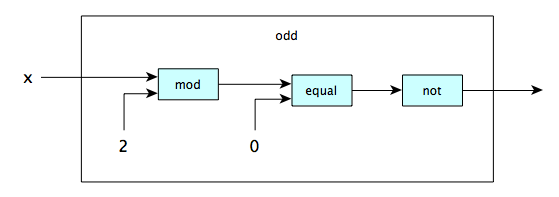
To define a function, we specify the rule that transforms the arguments into the result, often making use of existing functions. One way to do this is pictorially. Here we define a function to tell whether a number is odd:
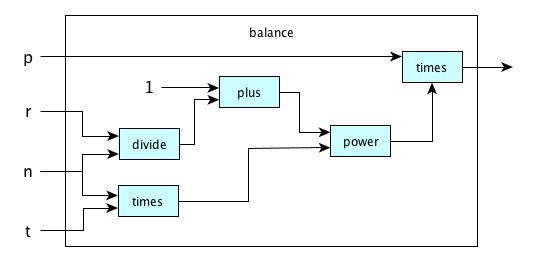
Here is a function that computes the balance of an account with starting principal value $p$, annual interest rate $r$, the number of compounding periods per year $n$, and the number of years $t$:
We can also use a more compact notation: start with a lambda, and separate the parameters from the rule with a dot. Examples:
λx.not(equal(mod(x, 2), 0))λ(p,n,r,t).times(p, power(plus(1, divide(r, n)), times(n, t)))
Sometimes we abbreviate functions. You’ve seen this, too:
- $\lambda x\,.\,x\:\textrm{mod}\:2 \neq 0$
- $\lambda (p,n,r,t)\,.\,p(1 + \frac{r}{n})^{nt}$
There are other notations, too:
(LAMBDA (x) (NOT (EQUAL (MOD X 2) 0)))(Lisp)lambda x: x % 2 != 0(Python)x => x % 2 != 0(JavaScript)(x) -> x % 2 != 0(Java)->(x) {x % 2 != 0}(Ruby)#(not= (mod % 2) 0)(Clojure){$0 % 2 != 0}(Swift)
Machines
We can build machines to execute functions—to capitalize text, find words in text, compute interest payments, etc. But functions can be written as text, so maybe we can build a machine (call it $U$), that when you give it a function $f$ (as text), and some data $x$, then $U$ will produce $f(x)$? That is: $$U(f,x) = f(x)$$
As it turns out, for a certain class of functions, you can construct such a machine. You might take that for granted today, but it was not obvious until the 20th century! (As far as anyone knows, that is.) This profound result is due to Alan Turing, and it pretty much changed the world. This $U$ is called the Universal Turing Machine in his honor. Today we build variations of the original $U$. We call them computers.
Programming
Thanks to Turing’s insights, it is possible to make machines that can compute just about anything. All we need is a way to describe a computation and then give that description together with some input data and tell your universal machine to simulate the computation.
The way you describe computations depends on your programming language. One very cool language is called Python. You can write and run Python many places online (for example here), or go to python.org and get yourself a Python interpreter for your own machine (unless you have one already).
Here is a program in Python that you can enter and run. It defines the two functions we’ve been looking at earlier, and calls them with various arguments.
def odd(x):
return x % 2 != 0
def balance(p, n, r, t):
return p * (1 + r/n) ** (n * t)
print(odd(-35))
print(odd(3278947239863000))
print(balance(1000, 12, 0.03, 5))
Computability
Here’s something we did not consider. Can every function be represented as a string of symbols that we can process with a machine?
It turns out that the answer to this is no.
Here’s why. First, if we want to describe functions for computing, we need a finite alphabet. (If you don’t buy that, think about it for a minute.) Now if the alphabet is finite, we can systematically list all programs in a countable fashion. There are a countably infinite number of possible programs. But the number of programs is uncountably infinite, which we’ll show by a diagonalization argument in class.
Bottom line:
Given any computing machine, there exist functions that it cannot compute.
Hey, this is philosophically interesting.
So which functions can be computed? Well, the Church-Turing Thesis says that the computable functions are precisely those for which a Turing Machine can be given, i.e.,
A function $f$ is computable if and only if a there exists a Turing Machine that outputs $f(x)$ for any input $x$.
To this day, no one has ever found a model of computation that can compute something that a Turing machine cannot. People have created other models of computation — the Lambda Calculus, Post Production Systems, Phrase Structure Grammars, Random Access Machines — but all have turned out to be equal in power (in terms of what they can compute) to the Turing machine. The Church-Turing thesis hypothesizes that no such model exists.
Now that function $U$ we saw before, the Universal Turing Machine, is so named because it can simulate any Turing Machine, and by the Church-Turing Thesis, any computable function.