Ohm

What is Ohm?
Ohm is advertised as a library for building parsers, interpreters, compilers, and more. With Ohm, you can quickly generate parsers simply by writing a grammar plus a couple lines of code. You can then write actions to operate on the nodes of the parser output to do whatever you like, such as:
- A compiler (with multiple targets, even!)
- An interpreter
- A semantics definition
- A syntax highlighter
Ohm enables your language’s formal syntax and a formal semantics to be truly executable—not just a bunch of static equations and rules in a PDF.
There’s even an interactive tool that enables to to interactively design grammars so that you can prototype new and beautiful programming languages. Woah.

Ohm Home Page
You can find all about Ohm, obtain the source code, read all of its documentation, and find links to tutorials, examples, real-world projects, and the community Discord server, at the home page.
Ohm Tutorial
Pat Dubroy, a co-creator of Ohm, wrote a nice tutorial. It’s worth a look as well.
Getting Started
Here’s a short video in which we:
- Introduce the Ohm Editor and design a grammar for a tiny programming language of arithmetic expressions and print statements
- Write an interpreter for this language so that one can run programs directly on the command line.
By the way: if you can write a complete interpreter for a language, you can claim to have written a semantics—if you accept that it’s fine to say an interpreter is the semantics!
Here’s the result of the code-along from the video. If you did not watch the video, or don’t care to watch it, skip ahead to the Ohm Basics section.
import * as ohm from "ohm-js";
import * as fs from "fs";
const grammar = ohm.grammar(String.raw`PlusMinusLanguage {
Program = Statement+
Statement = "print" "(" Exp ")" ";"
Exp = Exp "+" Term --plus
| Exp "-" Term --minus
| Term
Term = "(" Exp ")" --parens
| num
num = digit+
}`);
const interpreter = grammar.createSemantics().addOperation("eval", {
Program(statements) {
for (const statement of statements.children) {
statement.eval();
}
},
Statement(_print, _leftParen, expression, _rightParen, _semicolon) {
console.log(expression.eval());
},
Exp_plus(left, _plus, right) {
return left.eval() + right.eval();
},
Exp_minus(left, _plus, right) {
return left.eval() - right.eval();
},
Term_parens(_leftParen, expression, _rightParen) {
return expression.eval();
},
num(digits) {
return Number(digits.sourceString);
},
});
const match = grammar.match(fs.readFileSync(process.argv[2]));
if (match.failed()) {
console.error(match.message);
} else {
interpreter(match).eval();
}
Ohm Basics
The best way to get started is to use the amazing Ohm Editor. While composing your grammar, write and execute lots of test cases for both legal and illegal constructs. The tests will light up green for success and red for failure as you type. The parse tree will also appear as you type. The immediate feedback cycle is the best way to create.
Watch the video above for details, or if you prefer to save yourself the watching time and just want to read, try out the following famous grammar for starters:
Arithmetic {
Exp = Plus | Minus | num
Plus = Exp "+" num
Minus = Exp "-" num
num = digit+
}
Write some test cases and explore the parse trees. Note how the operators are left associative.
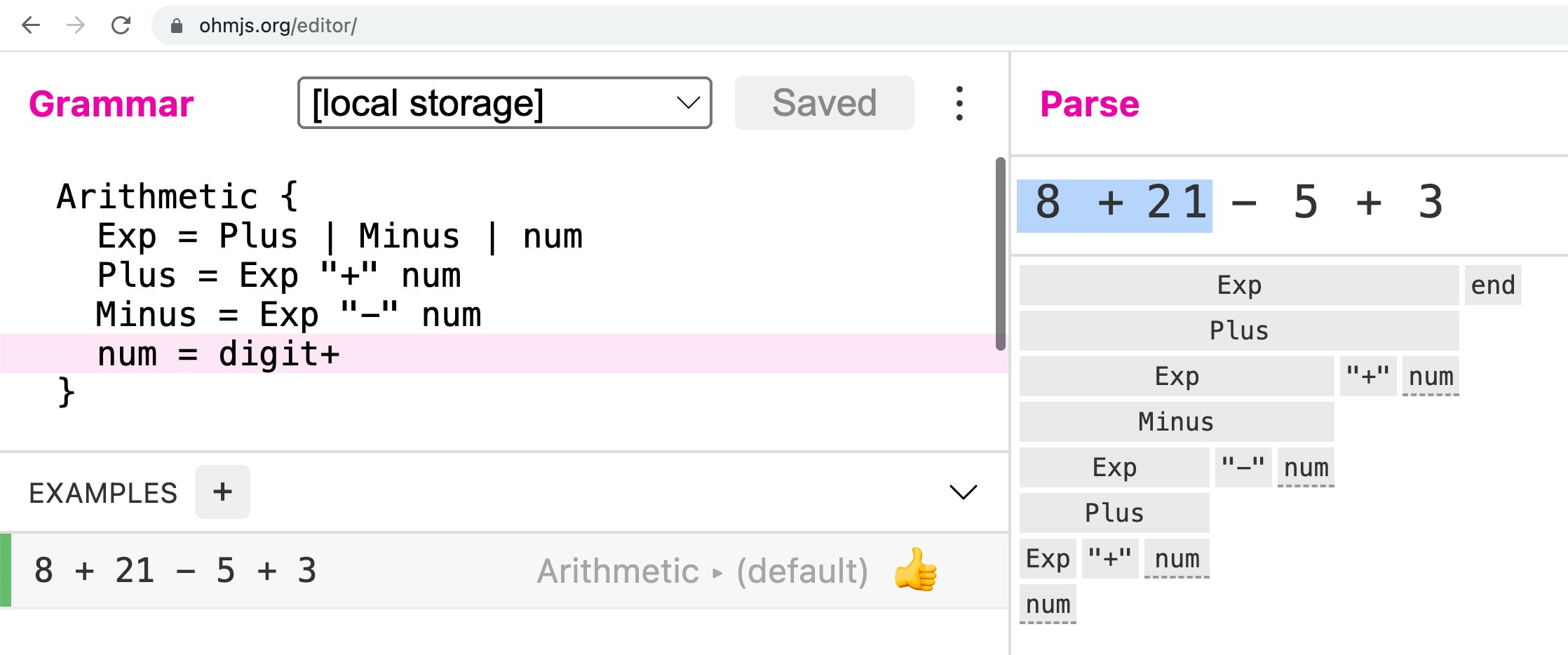
Now, let’s go through the basics in more detail, and build an actual interpreter!
Setting up a Project
Let’s make an interpreter for a real programming language, Astro. Begin as you would to make any Node.js project (with a recent version of Node.js, of course):
$ mkdir astro-interpreter $ cd astro-interpreter $ npm init -y
Then edit package.json to have a top-level property "type": "module".
Include Ohm in your project:
$ npm install ohm-js
Check package.json to make sure the Ohm package has been added to the dependencies section.
Writing a Grammar
Create the file astro.ohm and populate it with the grammar:
Astro {
Program = Statement+
Statement = id "=" Exp ";" --assignment
| print Exp ";" --print
Exp = Exp ("+" | "-") Term --binary
| Term
Term = Term ("*" | "/" | "%") Factor --binary
| Factor
Factor = Primary "**" Factor --binary
| "-" Primary --negation
| Primary
Primary = id "(" ListOf<Exp, ","> ")" --call
| numeral --num
| id --id
| "(" Exp ")" --parens
numeral = digit+ ("." digit+)? (("E" | "e") ("+" | "-")? digit+)?
print = "print" ~idchar
idchar = letter | digit | "_"
id = ~print letter idchar*
space += "//" (~"\n" any)* --comment
}
Design with the Ohm Editor
Especially when working with larger languages, the process of interactively designing with a live tool like the Ohm Editor is pretty much a necessity. Once designed, you’ll want to grab your grammar from the editor window and put it into a real software project.
Understanding Parsing Expressions
Ohm grammars consist of a name and a list of rules, the bodies of which are known as parsing expressions. Details are in the syntax reference, which you need to eventually read. But as you may be impatient, here are the Ohm parsing expressions:
| Expression | Description |
|---|---|
"..." | A literal string. Allows the usual escape chars \', \", \b, \n, \r, \t, \f, \\, \x$hh$, \u$hhhh$, and \u{$h...h$}.
|
| $rulename$ | Just a rule. |
$rulename$<$params$> | A rule with parameters. |
$e$* | $e$, zero or more times. |
$e$+ | $e$, one or more times. |
$e$? | $e$, zero or one times. |
| $e_1\;e_2$ | Match $e_1$ then match $e_2$. |
| $e_1\;|\;e_2$ | If $e_1$ matches, great. Otherwise try to match $e_2$. |
&$e$ | Match $e$ without consuming it (lookahead). |
~$e$ | Succeed if $e$ doesn’t match, without consuming anything (negative lookahead). |
#$e$ | Lexify a syntactic rule. |
Understanding Lexical and Syntax Rules
Lexical rules always start with lower case letters and syntax rules start with uppercase letters. Syntax rules allow tokens from the classspace to be implicitly interspersed with other tokens.
Built-In Rules
There are several built-in rules:
any =any char at allend =the end of the inputspace = " " | "\x09".."\x0d" | "\ufeff" |any char from Unicode category Zsdigit = "0".."9"lower =any char from Unicode category Llupper =any char from Unicode category LuunicodeLtmo =any char from Unicode category Lt, Lm, or Loletter = lower | upper | unicodeLtmoalnum = letter | digithexDigit = digit | "A".."F" | "a".."f"caseInsensitive<t> =any case insensitive version of temptyListOf<elem, sep> = /* nothing */nonemptyListOf<elem, sep> = elem (sep elem)*listOf<elem, sep> = nonemptyListOf<elem, sep> | emptyListOf<elem, sep>EmptyListOf<elem, sep> = /* nothing */NonemptyListOf<elem, sep> = elem (sep elem)*ListOf<elem, sep> = NonemptyListOf<elem, sep> | EmptyListOf<elem, sep>
Rule Arities are Important in Ohm
All alternatives for a rule must have the same arity. This is a small price to pay for the massive advantage you get from separating the grammar from the parsing actions that we will see later. But there is a cool short-hand to make it look like alternatives with different arities exist. For example:
Exp = Exp "+" Term --plus
| Exp "-" Term --minus
| Term
is an abbreviation for:
Exp = Exp_plus | Exp_minus | Term
Exp_plus = Exp "+" Term
Exp_minus = Exp "-" Term
Grammar Inheritance
Grammars can inherit from other grammars. When inheriting, use:
=to add a new rule:=to replace the rule from the supergrammar+=to add an alternative to the rule from the supergrammar
Any grammar you write yourself automatically inherits from the base Ohm grammar, where the built-in rules are defined.
Match Results
Given a grammar $g$ and source code $c$, $g$.match($c$) returns a MatchResult object, $m$. If $m$.succeeded() is true, $m$ wraps a parse tree, and you can apply a semantics object to it. If $m$.failed() is true, a detailed error message will be in $m$.message and a smaller error message will be in $m$.shortMessage.
In the Astro interpreter we’re building, create the file astro.js. This file will house the program. We can get started by populating it with:
import * as ohm from "ohm-js"
import fs from "fs"
const astroGrammar = ohm.grammar(fs.readFileSync("astro.ohm"))
const match = astroGrammar.match(process.argv[2])
if (match.failed()) throw new Error(match.message)
console.log("Syntax ok")
In your terminal, invoke
$ node astro.js 'print(3 + 5.5);'
And you should see the response:
Syntax ok
Applying Semantics
Once we have a parse tree we can process it with what Ohm calls a semantics object. You can write a semantics object to do anything you want with your parse tree, which is why Ohm is awesome.
Ohm’s SuperpowerIn other language processing libraries, like ANTLR and Bison, semantic processing rules are embedded inside the grammar. Ohm clearly separates them. This makes it easy in Ohm to write many sets of semantic actions for a single grammar.
The thing we are going to do is write an interpreter.
A semantics object is a collection of operations and attributes. Operations and attributes are applied to each node in the parse tree. Operations and attributes are similar: operations are functions (called every time), and attributes are memoized and called with property syntax. You generally define how operations and attributes behave for each of your rules, but you don’t have to define these for every rule because Ohm provides for defaults. Let’s just jump right in to adding an interpreter to our running example, which we’ll develop and explain in a class code-along.
Here’s the complete astro.js:
import * as ohm from "ohm-js"
import * as fs from "fs"
const astroGrammar = ohm.grammar(fs.readFileSync("astro.ohm"))
const memory = {
π: { type: "NUM", value: Math.PI, mutable: false },
sin: { type: "FUNC", fun: Math.sin, paramCount: 1 },
cos: { type: "FUNC", fun: Math.cos, paramCount: 1 },
sqrt: { type: "FUNC", fun: Math.sqrt, paramCount: 1 },
hypot: { type: "FUNC", fun: Math.hypot, paramCount: 2 },
}
function must(condition, message, at) {
if (!condition) throw new Error(`${at.source.getLineAndColumnMessage()}${message}`)
}
const evaluator = astroGrammar.createSemantics().addOperation("eval", {
Program(statements) {
for (const statement of statements.children) statement.eval()
},
Statement_assignment(id, _eq, expression, _semicolon) {
const entity = memory[id.sourceString]
must(!entity || entity?.type === "NUM", "Cannot assign", id)
must(!entity || entity?.mutable, `${id.sourceString} not writable`, id)
memory[id.sourceString] = { type: "NUM", value: expression.eval(), mutable: true }
},
Statement_print(_print, expression, _semicolon) {
console.log(expression.eval())
},
Exp_binary(left, op, right) {
const [x, y] = [left.eval(), right.eval()]
return op.sourceString == "+" ? x + y : x - y
},
Term_binary(left, op, right) {
const [x, o, y] = [left.eval(), op.sourceString, right.eval()]
return o == "*" ? x * y : o == "/" ? x / y : x % y
},
Factor_binary(left, _op, right) {
return left.eval() ** right.eval()
},
Primary_parens(_leftParen, e, _rightParen) {
return e.eval()
},
Primary_num(num) {
return Number(num.sourceString)
},
Primary_id(id) {
const entity = memory[id.sourceString]
must(entity !== undefined, `${id.sourceString} not defined`, id)
must(entity?.type === "NUM", `Expected type number`, id)
return entity.value
},
Primary_call(id, _open, exps, _close) {
const entity = memory[id.sourceString]
must(entity !== undefined, `${id.sourceString} not defined`, id)
must(entity?.type === "FUNC", "Function expected", id)
const args = exps.asIteration().children.map(e => e.eval())
must(args.length === entity?.paramCount, "Wrong number of arguments", exps)
return entity.fun(...args)
},
})
try {
const match = astroGrammar.match(process.argv[2])
if (match.failed()) throw new Error(match.message)
evaluator(match).eval()
} catch (e) {
console.error(`${e}`)
}
Lots to explain here!
Running the Interpreter
Let's see the program in action:
$ node astro.js 'print(3 + 5.5);'
8.5
$ node astro.js 'x = 5;
y = 3;
print(x ** y * sqrt(100));'
1250
$ node astro.js '
dozen = 5 + 8 - 1;
print(dozen ** 3 / sqrt(100));
print(sqrt(5.9 + hypot(π, 3.5e-8)));
'
172.8
3.0069241183624493
$ node astro.js '
print(5);
print(x - 10);
y = 100 + x;'
5
Error: Line 3, col 8:
2 | print(5);
> 3 | print(x - 10);
^
4 | y = 100 + x;
x not defined
Note the interpreter accepts the program to interpret as a command line argument. If your Astro program were in a file (say, hello.astro) you can still run the interpreter with:
$ cat hello.astro | xargs -0 node astro.js
Understanding Action Dictionaries
To a grammar, you attach a semantics object. To a semantics object, you can attach operations and attributes. The main property of an operation is an object called an action dictionary. The methods of the action dictionary correspond to rules of your grammar, with the left hand side as the method name and the right hand side as the method parameters, which are parse nodes. We saw this above.
We need practice. And more examples. Here’s a sample grammar that illustrates the important things to know:
Sample {
S = A B* C+ D? ListOf<E, ","> f
...
}
Let’s set up a semantics object with an operation called rep:
const semantics = grammar.createSemantics().addOperation("rep", { ... })
To define the operation rep, we create a method for S. It will have six parameters (because there are six “things” on the right hand side of the rule for S), each of which are provided to us by Ohm as parse nodes. There are three types of parse nodes: (1) rule application nodes (for phrase rules), (2) terminal nodes (for lexical rules and literal strings), and (3) iteration nodes (when *, +, and ? are used):
S(a, bs, cs, ds, es, f) {
// a is a *rule application* node
// bs is an *iteration node* for the (0 or more) bs
// cs is an *iteration node* for the (1 or more) cs
// ds is an *iteration node* for the (0 or 1) ds
// es.asIteration() gets you the *iteration node* for the es
// f is a *terminal* node
}
In the body of S:
- Calling
a.rep()will invoke the methodA. - Calling
f.rep()will invoke the methodfif it exists; if it does not, then, becausefis a lexical rule, Ohm will invoke the special method_terminal. By default, an implementation of_terminalalready exists: it returnsthis.sourceString, but you can override this if you want. - Calling
bs.rep()will invoke the method_iteron the children ofbs. The method_iteris NOT defined by default! You could define it yourself like_iter(...children) { return children.map(c => c.rep()); }but it is much better to write things likemyNode.children.map(c => c.rep())directly each time you have to process an iteration node, since it makes clear to a reader that you have an iteration!
Don’t forget to use asIteration on your ListOf (and similar) nodes.
Official Documentation
These notes you are reading now are not exhaustive, but they will get you started! There is much more to Ohm. You will need to eventually check out the documentation.
Once you’re feeling pretty good, you will find the Syntax Reference, API Reference, and Patterns and Pitfalls most useful.
Time to move to examples.
Example Grammars
Let’s see Ohm in use with a few examples of our own. (There are more in the GitHub repo for Ohm.)
We’ll be going through these line by line, discussing not only Ohm specifics, but also a bit about language design in general and the intended meaning of each syntactic construct.
Bella
Bella is one of the example languages for this class. Here is its Ohm grammar:
Bella {
Program = Statement+
Statement = let id "=" Exp ";" -- vardec
| function id Params "=" Exp ";" -- fundec
| Exp7_id "=" Exp ";" -- assign
| print Exp ";" -- print
| while Exp Block -- while
Params = "(" ListOf<id, ","> ")"
Block = "{" Statement* "}"
Exp = ("-" | "!") Exp7 -- unary
| Exp1 "?" Exp1 ":" Exp -- ternary
| Exp1
Exp1 = Exp1 "||" Exp2 -- binary
| Exp2
Exp2 = Exp2 "&&" Exp3 -- binary
| Exp3
Exp3 = Exp4 ("<="|"<"|"=="|"!="|">="|">") Exp4 -- binary
| Exp4
Exp4 = Exp4 ("+" | "-") Exp5 -- binary
| Exp5
Exp5 = Exp5 ("*" | "/" | "%") Exp6 -- binary
| Exp6
Exp6 = Exp7 "**" Exp6 -- binary
| Exp7
Exp7 = num
| true
| false
| id "(" ListOf<Exp, ","> ")" -- call
| id -- id
| "(" Exp ")" -- parens
let = "let" ~idchar
function = "function" ~idchar
while = "while" ~idchar
true = "true" ~idchar
false = "false" ~idchar
print = "print" ~idchar
keyword = let | function | while | true | false
num = digit+ ("." digit+)? (("E" | "e") ("+" | "-")? digit+)?
id = ~keyword letter idchar*
idchar = letter | digit | "_"
space += "//" (~"\n" any)* -- comment
}
Carlos
Carlos is another language for this class. It’s a bit more sophisticated than Bella.
Carlos {
Program = Statement+
Statement = VarDecl
| TypeDecl
| FunDecl
| Exp9 ("++" | "--") ";" --bump
| Exp9 "=" Exp ";" --assign
| Exp9_call ";" --call
| break ";" --break
| return Exp ";" --return
| return ";" --shortreturn
| IfStmt
| LoopStmt
VarDecl = (let | const) id "=" Exp ";"
TypeDecl = struct id "{" Field* "}"
Field = id ":" Type
FunDecl = function id Params (":" Type)? Block
Params = "(" ListOf<Param, ","> ")"
Param = id ":" Type
Type = Type "?" --optional
| "[" Type "]" --array
| "(" ListOf<Type, ","> ")" "->" Type --function
| id --id
IfStmt = if Exp Block else Block --long
| if Exp Block else IfStmt --elsif
| if Exp Block --short
LoopStmt = while Exp Block --while
| repeat Exp Block --repeat
| for id in Exp ("..." | "..<") Exp Block --range
| for id in Exp Block --collection
Block = "{" Statement* "}"
Exp = Exp1 "?" Exp1 ":" Exp --conditional
| Exp1
Exp1 = Exp1 "??" Exp2 --unwrapelse
| Exp2
Exp2 = Exp3 ("||" Exp3)+ --or
| Exp3 ("&&" Exp3)+ --and
| Exp3
Exp3 = Exp4 ("|" Exp4)+ --bitor
| Exp4 ("^" Exp4)+ --bitxor
| Exp4 ("&" Exp4)+ --bitand
| Exp4
Exp4 = Exp5 ("<="|"<"|"=="|"!="|">="|">") Exp5 --compare
| Exp5
Exp5 = Exp5 ("<<" | ">>") Exp6 --shift
| Exp6
Exp6 = Exp6 ("+" | "-") Exp7 --add
| Exp7
Exp7 = Exp7 ("*"| "/" | "%") Exp8 --multiply
| Exp8
Exp8 = Exp9 "**" Exp8 --power
| Exp9
| ("#" | "-" | "!" | some | random) Exp9 --unary
Exp9 = true ~mut
| false ~mut
| floatlit ~mut
| intlit ~mut
| no Type ~mut --emptyopt
| Exp9 "(" ListOf<Exp, ","> ")" ~mut --call
| Exp9 "[" Exp "]" --subscript
| Exp9 ("." | "?.") id --member
| stringlit ~mut
| id --id
| Type_array "(" ")" ~mut --emptyarray
| "[" NonemptyListOf<Exp, ","> "]" ~mut --arrayexp
| "(" Exp ")" ~mut --parens
intlit = digit+
floatlit = digit+ "." digit+ (("E" | "e") ("+" | "-")? digit+)?
stringlit = "\"" char* "\""
char = ~control ~"\\" ~"\"" any
| "\\" ("n" | "t" | "\"" | "\\") --escape
| "\\u{" hex hex? hex? hex? hex? hex? "}" --codepoint
control = "\x00".."\x1f" | "\x80".."\x9f"
hex = hexDigit
mut = ~"==" "=" | "++" | "--"
let = "let" ~alnum
const = "const" ~alnum
struct = "struct" ~alnum
function = "function" ~alnum
if = "if" ~alnum
else = "else" ~alnum
while = "while" ~alnum
repeat = "repeat" ~alnum
for = "for" ~alnum
in = "in" ~alnum
random = "random" ~alnum
break = "break" ~alnum
return = "return" ~alnum
some = "some" ~alnum
no = "no" ~alnum
true = "true" ~alnum
false = "false" ~alnum
keyword = let | const | struct | function | if | else | while | repeat
| for | in | break | return | some | no | random | true | false
id = ~keyword letter alnum*
space += "//" (~"\n" any)* --comment
}
Dax
Dax is a made up functional language.
Dax {
Program = Exp
Exp = ("-" | "!") Primary --unary
| Exp0 then Exp --then
| Exp0
Exp0 = Exp0 "|>" Exp1 --pipe
| Exp1
Exp1 = Exp2 "?" Exp2 ":" Exp1 --ternary
| Exp2
Exp2 = Exp3 ("&&" Exp3)+ --and
| Exp3 ("||" Exp3)+ --or
| Exp3
Exp3 = Exp4 relop Exp4 --compare
| Exp4
Exp4 = Exp4 ("+" | "-") Term --addsub
| Term
Term = Term ("*" | "/" | "%") Factor --muldiv
| Factor
Factor = Primary "**" Factor --exponent
| Primary
Primary = num
| true
| false
| stringlit
| let Dec (";" Dec)* in Exp kwend --let
| id Primary+ --id_call
| id --id
| "(" Exp ")" Primary+ --paren_call
| "(" Exp ")" --paren
| "[" ListOf<Exp, ","> "]" --array
| "{" id "=>" Exp "}" Primary+ --lambda_call
| "{" id "=>" Exp "}" --lambda
Dec = id "=" Exp
relop = "<=" | "<" | "==" | "!=" | ">=" | ">"
then = "then" ~idchar
let = "let" ~idchar
in = "in" ~idchar
kwend = "end" ~idchar
true = "true" ~idchar
false = "false" ~idchar
keyword = then | let | in | kwend | true | false
id = ~keyword letter idchar*
idchar = letter | digit | "_"
num = digit+ ("." digit+)? (("E" | "e") ("+" | "-")? digit+)?
stringlit = "\"" char* "\""
char = ~control ~"\\" ~"\"" any
| "\\" ("n" | "t" | "\"" | "\\") --escape
| "\\u{" hex hex? hex? hex? hex? hex? "}" --codepoint
control = "\x00".."\x1f" | "\x80".."\x9f"
hex = hexDigit
space += "//" (~"\n" any)* "\n" -- comment
}
A Java-like scripting language
Here is a small scripting language that is very Java-like in appearance, with a few simplifying features: (1) there are no classes, (2) the language needs little if any type inference, and (3) the standard library is both package-less and microscopic:
TinyJava {
Program = Stmt+
Stmt = Dec -- declaration
| Assignment ";" -- assignment
| Call ";" -- call
| break ";" -- break
| return Exp? ";" -- return
| print Args ";" -- print
| if Exp Block
(else if Exp Block)*
(else Block)? -- if
| while Exp Block -- while
| for "("
(Type id "=" Exp)? ";"
Exp? ";"
Assignment? ")"
Block -- for
Assignment = Increment -- increment
| Var "=" Exp -- plain
Increment = incop Var -- prefix
| Var incop -- postfix
Dec = TypeDec | VarDec | FunDec
TypeDec = struct id "{"
(Type id ";")*
"}"
Type = Type "[" "]" -- array
| primtype
| id
VarDec = Type id ("=" Exp)? ";"
FunDec = (Type | void) id "(" Params ")" Block
Params = (Type id ("," Type id)*)?
Block = "{" Stmt* "}"
Exp = NonemptyListOf<Exp1, "||">
Exp1 = NonemptyListOf<Exp2, "&&">
Exp2 = NonemptyListOf<Exp3, "|">
Exp3 = NonemptyListOf<Exp4, "^">
Exp4 = NonemptyListOf<Exp5, "&">
Exp5 = Exp6 (relop Exp6)?
Exp6 = NonemptyListOf<Exp7, shiftop>
Exp7 = NonemptyListOf<Exp8, addop>
Exp8 = NonemptyListOf<Exp9, mulop>
Exp9 = prefixop? Exp10
Exp10 = Literal
| Increment
| Var
| NewObject
| NewArray
| EmptyArray
| "(" Exp ")" -- parens
Literal = null
| true
| false
| floatlit
| intlit
| charlit
| stringlit
Var = Var "[" Exp "]" -- subscript
| Var "." id -- select
| Call
| id
NewObject = new id "{" Args "}"
NewArray = new Type_array "{" Args "}"
EmptyArray = new Type "[" Exp "]"
Call = id "(" Args ")"
Args = ListOf<Exp, ",">
boolean = "boolean" ~idchar
break = "break" ~idchar
char = "char" ~idchar
else = "else" ~idchar
false = "false" ~idchar
for = "for" ~idchar
if = "if" ~idchar
int = "int" ~idchar
length = "length" ~idchar
new = "new" ~idchar
null = "null" ~idchar
print = "print" ~idchar
real = "real" ~idchar
return = "return" ~idchar
string = "string" ~idchar
return = "return" ~idchar
struct = "struct" ~idchar
true = "true" ~idchar
void = "void" ~idchar
while = "while" ~idchar
keyword = boolean | if | break | else | int | for | new
| return | char | struct | null | while | real
| true | string | void | false | length | print
id = ~keyword letter idchar*
idchar = "_" | alnum
intlit = digit+
floatlit = digit+ "." digit+ (("E"|"e") ("+"|"-")? digit+)?
char = escape
| ~"\\" ~"\"" ~"'" ~"\n" any
h = hexDigit
escape = "\\\\" | "\\\"" | "\\'" | "\\n" | "\\t" | hexseq
hexseq = "\\" h h? h? h? h? h? h? h? ";"
charlit = "'" (char | "\"") "'"
stringlit = "\"" (char | "\'")* "\""
addop = "+" | "-"
relop = "<=" | "<" | "==" | "!=" | ">=" | ">"
shiftop = "<<" | ">>"
mulop = "*" | "/" | "%"
prefixop = ~"--" "-" | "!" | "~" | char | int | string | length
incop = "++" | "--"
primtype = boolean | char | int | real | string
space := "\x20" | "\x09" | "\x0A" | "\x0D" | comment
comment = "//" (~"\n" any)*
}
JavaScript
Yes, there is a full ECMAScript grammar in Ohm out there.
Brainfuck
Brainfuck has a pretty trivial grammar. There are eight one-character instructions, and every other character is ignored.
Brainfuck {
Program = instruction+
instruction = "[" instruction* "]" -- loop
| "," | "." | "+" | "-" | "<" | ">"
space = ~instruction any
}
Example Applications
Ohm can do so much more—so much more—than just generate ASTs. You can do just about anything in the semantics (parsing functions). Here are a few case studies:
Infix to Postfix Conversion
Here is a language of infix arithmetic expressions over numbers and identifiers. From lowest to highest the precedences are: (1) the left-associative additive operators, (2) left-associative multiplicative operators, (3) the prefix unary negation operator, (4) right-associative the exponentiation operator.
import * as ohm from 'ohm-js'
const grammar = ohm.grammar(`Infix {
Program = Exp
Exp = Exp ("+" | "-") Term --binary
| Term
Term = Term ("*" | "/") Factor --binary
| Factor
Factor = "-" Factor --negate
| Primary "**" Factor --binary
| Primary
Primary = "(" Exp ")" --parens
| digit+ --number
| letter alnum* --identifier
}`)
const semantics = grammar.createSemantics().addOperation('post', {
Program(body) {
return body.post()
},
Exp_binary(left, op, right) {
return `${left.post()} ${right.post()} ${op.sourceString}`
},
Term_binary(left, op, right) {
return `${left.post()} ${right.post()} ${op.sourceString}`
},
Factor_binary(left, op, right) {
return `${left.post()} ${right.post()} ${op.sourceString}`
},
Factor_negate(_op, operand) {
return `${operand.post()} ~`
},
Primary_parens(_open, expression, _close) {
return expression.post()
},
Primary_number(_chars) {
return this.sourceString
},
Primary_identifier(_first, _rest) {
return this.sourceString
},
})
export function toPostfix(infix) {
let match = grammar.match(infix)
if (!match.succeeded()) {
throw new Error(match.message)
}
return semantics(match).post()
}
Unit tests:
import { describe, it } from "node:test"
import assert from "assert/strict"
import { toPostfix } from "../infix-to-postfix.mjs"
describe("When converting infix to postfix", () => {
it("works", () => {
assert.equal(toPostfix("1 + 2"), "1 2 +")
assert.equal(toPostfix("1 + 2 - 3"), "1 2 + 3 -")
assert.equal(toPostfix("1 ** 2 ** 3"), "1 2 3 ** **")
assert.equal(toPostfix("-1 ** 2 ** 3"), "1 2 3 ** ** ~")
})
})
Run the tests with a command such as node --test test/infix-to-postfix-test.mjs
Evaluating and Differentiating Polynomials 😍
This fun script illustrates multiple semantics for the same grammar.
import * as ohm from 'ohm-js'
const grammar = ohm.grammar(`Polynomial {
Poly
= Poly "+" term -- add
| Poly "-" term -- subtract
| "-" Poly -- negate
| term
term
= coefficient "x^" exponent -- coeff_var_exp
| coefficient "x" -- coeff_var
| coefficient -- coeff
| "x^" exponent -- var_exp
| "x" -- var
coefficient
= digit+ ("." digit+)?
exponent
= "-"? digit+
}`)
/* eslint-disable no-unused-vars */
const semantics = grammar
.createSemantics()
.addOperation('deriv', {
Poly_add(p, op, t) {
return `${p.deriv()}+${t.deriv()}`
},
Poly_subtract(p, op, t) {
return `${p.deriv()}-${t.deriv()}`
},
Poly_negate(_, p) {
return `-${p.deriv()}`
},
term_coeff_var_exp(c, _, e) {
return `${e.value * c.value}x^${e.value - 1}`
},
term_coeff_var(c, _) {
return `${c.value}`
},
term_coeff(c) {
return '0'
},
term_var_exp(_, e) {
return `${e.value}x^${e.value - 1}`
},
term_var(_) {
return '1'
},
})
.addOperation('eval', {
Poly_add(p, op, t) {
return x => p.eval()(x) + t.eval()(x)
},
Poly_subtract(p, op, t) {
return x => p.eval()(x) - t.eval()(x)
},
Poly_negate(_, p) {
return x => -p.eval()(x)
},
term_coeff_var_exp(c, _, e) {
return x => c.value * x ** e.value
},
term_coeff_var(c, _) {
return x => c.value * x
},
term_coeff(c) {
return x => c.value
},
term_var_exp(_, e) {
return x => x ** e.value
},
term_var(_) {
return x => x
},
})
.addAttribute('value', {
coefficient(whole, dot, fraction) {
return +this.sourceString
},
exponent(sign, magnitude) {
return +this.sourceString
},
})
export function derivative(poly) {
const match = grammar.match(poly)
if (!match.succeeded()) {
throw new Error(match.message)
}
return semantics(match).deriv()
.replace(/\-\-/g, '+')
.replace(/\+\-/g, '-')
.replace(/^\+/, '')
.replace(/\+0(?!\d)/, '')
.replace(/\^1(?!\d)$/, '')
}
export function evaluate(poly, x) {
const match = grammar.match(poly)
if (!match.succeeded()) {
throw new Error(match.message)
}
return semantics(match).eval()(x)
}
With unit tests even!
import { describe, it } from "node:test"
import assert from "assert/strict"
import { derivative, evaluate } from "../polynomial.mjs"
describe("The differentiator", () => {
it("detects malformed polynomials", () => {
assert.throws(() => derivative("2y"))
assert.throws(() => derivative("blah"))
assert.throws(() => derivative("2x*6"))
})
it("correctly differentiates single-term polynomials", () => {
assert.equal(derivative("4"), "0")
assert.equal(derivative("2238"), "0")
assert.equal(derivative("x"), "1")
assert.equal(derivative("4x"), "4")
assert.equal(derivative("x^5"), "5x^4")
assert.equal(derivative("2x^-4"), "-8x^-5")
})
it("correctly differentiates multi-term polynomials", () => {
assert.equal(derivative("-4"), "-0")
assert.equal(derivative("-2238"), "-0")
assert.equal(derivative("-x"), "-1")
assert.equal(derivative("-x^5"), "-5x^4")
assert.equal(derivative("-x^-5"), "5x^-6")
assert.equal(derivative("2x^-4 + 7x^2"), "-8x^-5+14x")
assert.equal(derivative(" 2x^-4- 7x^20"), "-8x^-5-140x^19")
assert.equal(derivative("2x^-4 +7x^-2"), "-8x^-5-14x^-3")
})
})
describe("The evaluator", () => {
it("detects malformed polynomials", () => {
assert.throws(() => evaluate("2y"))
assert.throws(() => evaluate("blah"))
assert.throws(() => evaluate("2x*6"))
})
it("correctly evaluates single-term polynomials", () => {
assert.equal(evaluate("4", 5), 4)
assert.equal(evaluate("2238", 19), 2238)
assert.equal(evaluate("x", 3), 3)
assert.equal(evaluate("4x", 10), 40)
assert.equal(evaluate("x^5", 2), 32)
assert.equal(evaluate("32x^-4", 2), 2)
})
it("correctly evaluates complex polynomials", () => {
assert.equal(evaluate("-4", 8), -4)
assert.equal(evaluate("-2238", 11), -2238)
assert.equal(evaluate("-x", 5), -5)
assert.equal(evaluate("-x^5", 3), -243)
assert.equal(evaluate("-x^-3", 2), -0.125)
assert.equal(evaluate("2x^8 + 7x^2", 2), 540)
assert.equal(evaluate(" 2x^3- 7x^1", 4), 100)
assert.equal(evaluate("2x^3 +7x^1", 4), 156)
})
})
We’ll build a command line application allowing differentiation and evaluation of polynomials. Should be fun!
Complete Compilers
Compilers for the languages Bella and Carlos above, targeting JavaScript, can be found at GitHub here and here. Feel free to fork the projects, modify or extend the languages, and experiment with Ohm.
The compilers have unit tests and 100% coverage.
More Examples
The Ohm repository on GitHub has a nice list of examples.
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- What can you do with Ohm? (1) Define the syntax and semantics of a language, and (2) easily write parsers, interpreters, compilers, and more.
- Why is the Ohm Editor useful? It allows for an interactive programming language design by providing immediate feedback as you author the grammar.
- What is the difference between
xand"x"in Ohm rules?xis a rule,"x"is a literal. - What is the difference between lexical and syntax rules in Ohm? Lexical rules are for tokens, syntax rules are for phrases that are allowed to implicitly have spaces between components.
- What does the parsing expression
e1 | e2mean?Try to matche1, and if that fails, try to matche2. - What does the parsing expression
e*mean?Matchezero or more times. - What does the parsing expression
e+mean?Matcheone or more times. - What does the parsing expression
e?mean?Matchezero or one times. - What does the parsing expression
&emean?Matchewithout consuming it (positive lookahead). - What does the parsing expression
~emean?Succeed ifedoesn’t match, without consuming anything (negative lookahead). - What is the built-in rule that matches the end of the input in Ohm?
end - How do you represent “any character except a newline” in Ohm?
~"\n" any - Why does Ohm require each branch of an alternation to have the same arity? So that parsing actions can take a fixed number of parameters.
- What cool shorthand does Ohm allow so that you don’t have to explicitly created separate related rules to make sure arity restrictions are followed? You can use
--labelat the end of alternatives. - How to do bring in the Ohm library in a JavaScript application?
import * as ohm from "ohm-js" - How does the
matchmethod on an Ohm grammar object work?It returns aMatchResultobject that wraps a parse tree if the match succeeded. - What are the main methods and properties of an Ohm MatchResult?
succeeded(),failed(),message,shortMessage. - How do you obtain a semantics object for a grammar $g$ in Ohm?
g.createSemantics() - What is the difference between operations and attributes in an Ohm semantics object? Operations are functions that are called every time, attributes are memoized and called with property syntax.
- What are the three kinds of parse nodes in Ohm? Rule application nodes, iteration nodes, terminal nodes.
- If you call an action method on a terminal node, but there is no associated method in the action dictionary, what happens? The special method
_terminalis called, which by default returnsthis.sourceString. - If you call an action method on an iteration node, but there is no associated method in the action dictionary, what happens? You will get an error, unless you have properly defined an
_itermethod in the dictionary. - Is it a best practice to fall back to the
_itermethod?No, it is better to writemyNode.children.map(c => c.rep())directly each time you have to process an iteration node.
Summary
We’ve covered:
- A good deal about Ohm
- Where to find Ohm’s documentation
- Example Ohm Grammars
- Examples of semantic processing in Ohm