Intermediate Representations
Motivation
An intermediate representation is any representation of a program “between” the source and target languages.
In a real compiler, you might see several intermediate representations!

A true intermediate representation is quite independent of the source and target languages, and yet very general, so that it can be used to build a whole family of compilers.
We use intermediate representations for at least four reasons:
- Because translation appears to inherently require analysis and synthesis. Word-for-word translation does not work. We need a conceptual model of the program, one that we can easily create from the source code, and one that is easy to construct target code from.
- To break the difficult problem of translation into two simpler, more manageable pieces.
- To build retargetable compilers:
- We can build new back ends for an existing front end (making the source language more portable across machines).
- We can build a new front-end for an existing back end (so a new machine can quickly get a set of compilers for different source languages).
- We only have to write $2n$ half-compilers instead of $n(n-1)$ full compilers. (Though this might be a bit of an exaggeration in practice!)
- To perform machine independent optimizations.
Flavors
Intermediate representations come in many flavors. The three main ones are:
Graph
Decorated and extended AST
Tuples
Code for an unbounded register machine
Stack
Code for a virtual stack machine
We’ll use a running example code fragment to illustrate various options.
while (x < 4 * y) {
x = y / 3 >> x;
if (y) print x - 3;
}
The so-called semantic graph is is just an abstract syntax tree, analyzed, type checked, annotated and transformed into a graph:
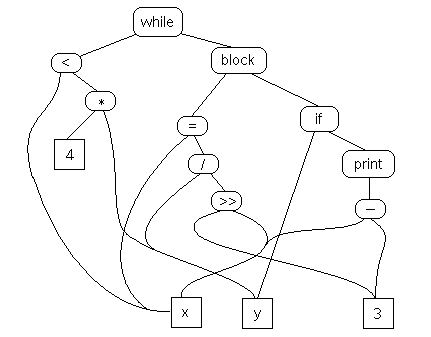
Some might not call this an IR, but rather simply a source program representation: it’s what the analyzer produces. You can even reconstruct the text of the source code from it (up to differences in whitespace and comments). Many folks would require a true IR to have some kind of lower level instruction lists. Tuples are the most common. Here is the tuple representation of the example source code fragment above:
(JUMP, L2) // goto L2 (LABEL, L1) // L1: (SHR, 3, x, t0) // t0 := 3 >> x (DIV, y, t0, t1) // t1 := y / t0 (COPY, t1, x) // x := t1 (JZ, y, L3) // if y == 0 goto L3 (SUB, x, 3, t2) // t2 := x - 3 (PRINT, t2) // print t2 (LABEL, L3) // L3: (LABEL, L2) // L2: (MUL, 4, y, t4) // t4 := 4 * y (LT, x, t4, t5) // t5 < t4 (JNZ, t5, L1) // if t5 != 0 goto L1
Another common form for an IR is stack code. Here’s how our running example might look:
JUMP L2
L1:
PUSH y
PUSHC 3
PUSH x
SHR
DIV
STORE x
PUSH y
JZERO L3
PUSH x
PUSHC 3
SUB
PRINT
L3:
L2:
PUSH x
PUSHC 4
PUSH y
MUL
LESS
JNOTZERO L1
Each flavor of IR (graph, stack, tuples) processes entities. Each entity in the IR is a bundle of information, which will be used in the later phases of the compiler that generate real target code. Entities are:
| Entity | Properties | Notes |
|---|---|---|
| Literal | value | Integer or floating-point constant. |
| Variable | name type owner | Variable or parameter from the source code. The owner is the function or module in which the variable or parameter was declared. |
| Subroutine | name parent parameters locals | Procedure or Function. |
| Temporary | name type | A temporary variable, generated while creating the IR. |
| Label | name | A label used for jumps. |
A type is i8, i16, i32, i64, i128, u8, u16, u32, u64, u128, f32, f64, f128, or similar. In an IR, all arguments are simple, meaning they all “fit“ in a machine word. Arrays, strings, and structs will be represented by their base address alone (so its type is up to you, perhaps i64). Elements and fields will be accessed by their offset from the base. Also, there are no fancy types, so booleans, chars, and enums will be represented as integers. An IR should be source language agnostic and target language agnostic.
Tuples
The nice thing about intermediate representations is that, because they are intermediate, they can be whatever you want. You can literally make up a set of tuples!
Tuples are instruction-like objects consisting of an operator and zero or more operands (defined above). A typical set of tuples might include:
| Tuple | Rendered as... | Description |
|---|---|---|
| (COPY,x,y) | y := x | Copy (a.k.a. Store) |
| (ADD,x,y,z) | z := x + y | Sum |
| (SUB,x,y,z) | z := x - y | Difference |
| (MUL,x,y,z) | z := x * y | Product |
| (DIV,x,y,z) | z := x / y | Quotient |
| (MOD,x,y,z) | z := x mod y | Modulo |
| (REM,x,y,z) | z := x rem y | Remainder |
| (POWER,x,y,z) | z := pow x, y | Exponentiation |
| (SHL,x,y,z) | z := x << y | Left shift |
| (SHR,x,y,z) | z := x >> y | Logical right shift |
| (SAR,x,y,z) | z := x >>> y | Arithmetic right shift |
| (AND,x,y,z) | z := x & y | Bitwise conjunction |
| (OR,x,y,z) | z := x | y | Bitwise disjunction |
| (XOR,x,y,z) | z := x xor y | Bitwise exclusive or |
| (NOT,x,y) | y := !x | Logical complement |
| (NEG,x,y) | y := -x | Negation |
| (COMP,x,y) | y := ~x | Bitwise complement |
| (ABS,x,y) | y := abs x | Absolute value |
| (SIN,x,y) | y := sin x | Sine |
| (COS,x,y) | y := cos x | Cosine |
| (ATAN,x,y,z) | z := atan x,y | Arctangent |
| (LN,x,y) | y := ln x | Natural logarithm |
| (SQRT,x,y) | y := sqrt x | Square root |
| (INC x) | inc x | Increment by 1; same as (ADD,x,1,x)
|
| (DEC,x) | dec x | Decrement by 1; same as (SUB,x,1,x)
|
| (LT,x,y,z) | z := x < y | 1 if x is less than y; 0 otherwise |
| (LE,x,y,z) | z := x <= y | 1 if x is less than or equal to y; 0 otherwise |
| (EQ,x,y,z) | z := x == y | 1 if x is equal to y; 0 otherwise |
| (NE,x,y,z) | z := x != y | 1 if x is not equal to y; 0 otherwise |
| (GE,x,y,z) | z := x >= y | 1 if x is greater than or equal to y; 0 otherwise |
| (GT,x,y,z) | z := x > y | 1 if x is greater than y; 0 otherwise |
| (MEM_ADDR,x,y) | y := &x | Copy address of x into y |
| (MEM_GET,x,y) | y := *x | Copy contents of memory at address x into y |
| (MEM_SET,x,y) | *y := x | Copy x into the memory at address y |
| (MEM_INC x) | inc *x | Increment a memory location given its address |
| (MEM_DEC,x) | dec *x | Decrement a memory location given its address |
| (ELEM_ADDR,a,i,x) | x := &(a[i]) | Copy address of a[i] into z; identical to (ADD, a, i*elsize, x) where elsize is the size in bytes of the element type of array a.
|
| (ELEM_GET,a,i,x) | x := a[i] | Copy contents of memory at address a + i*elsize into x; where elsize is the size in bytes of the element type of array a |
| (ELEM_SET,a,i,x) | a[i] := x | Copy x into the memory at address a + i*elsize; where elsize is the size in bytes of the element type of array a |
| (FIELD_ADDR,s,f,x) | x := &(s.f) | Copy address of s.f into x; identical to (ADD, s, ofs(f), x) where ofs(f) is the byte offset of field f in struct s.
|
| (FIELD_GET,s,f,x) | x := s.f | Copy contents of memory at address s + ofs(f) |
| (FIELD_SET,s,f,x) | s.f := x | Copy x into the memory at address s + ofs(f) |
| (LABEL,L) | L: | Label |
| (JUMP,L) | goto L | Unconditional jump to a label |
| (JZERO,x,L) | if x == 0 goto L | Jump if zero / Jump if false |
| (JNZERO,x,L) | if x != 0 goto L | Jump if zero / Jump if true |
| (JLT,x,y,L) | if x < y goto L | Jump if less / Jump if not greater or equal |
| (JLE,x,y,L) | if x <= y goto L | Jump if less or equal / Jump if not greater |
| (JEQ,x,y,L) | if x == y goto L | Jump if equal |
| (JNE,x,y,L) | if x != y goto L | Jump if not equal |
| (JGE,x,y,L) | if x >= y goto L | Jump if greater or equal / Jump if not less |
| (JGT,x,y,L) | if x > y goto L | Jump if greater / Jump if not less |
| (MULADD,x,y,z,w) | w := x + y*z | Multiply then add |
| (IJ,x,dx,L) | x := x + dx; goto L | Increment x then unconditionally jump |
| (IJE,x,dx,y,L) | x += dx; if x == y goto L | Increment and jump if equal (useful at end of for-loops that count up to a given value) |
| (DJNZ,x,L) | if --x != 0 goto L | Decrement and jump if not zero (great for loops that count down to zero by one) |
| (CALLP,f,x1,...,xn) | call f, x1, ..., xn | Call procedure (non-value returning function) f, with arguments x1, ..., xn |
| (CALLF,f,x1,...,xn,x) | x := call f, x1, ..., xn | Call function f, with arguments x1, ..., xn, and copy the result into x |
| (RETP) | ret | Return from procedure |
| (RETF,x) | ret x | Return x from this function |
| (INT_TO_STR,x,y) | y := to_string x | String representation of an integer (one can add a new tuple to take a base) |
| (FLOAT_TO_STR,x,y) | y := to_string x | String representation of a float (one can add a new tuple taking a format string) |
| (BOOL_TO_STR,x,y) | y := to_string x | String representation of a boolean (localized?) |
| (CHAR_TO_STR,x,y) | y := to_string x | String representation of a character |
| (ALLOC,x,y) | y := alloc x | Allocate x bytes of memory, returning the address in y (or 0 if the memory could not be allocated). |
| (ARRAY_ALLOC,x,y) | y := array_alloc x | Allocate x*elsize bytes of memory, where elsize is the number of bytes of an element in array x, returning the address in y (or 0 if the memory could not be allocated). |
| (DEALLOC,x) | dealloc x | Deallocate the memory at address x (or do nothing if x is 0) |
| (INT_TO_FLOAT,x,y) | y := to_float x | Integer to float |
| (ASSERT_NOT_NULL,x) (ASSERT_NONZERO,x) | assert x != 0 | Do something if x is null (details left to the implementation) |
| (ASSERT_POSITIVE,x) | assert x > 0 | Do something if x is not positive (details left to the implementation) |
| (ASSERT_BOUND,x,y,z) | assert y <= x < z | Do something if x is not between y (inclusive) and x (inclusive) (details left to the implementation) |
| (NO_OP) | nop | Do nothing |
| (EXIT,x) | exit | Terminate the program with error code x |
Arithmetic
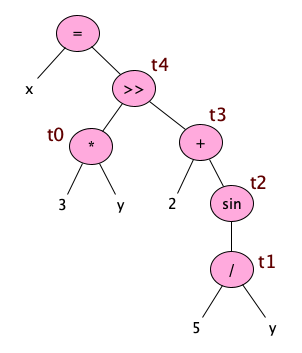
Note how tuples assume what is essentially an unlimited supply of registers. These are often called temporaries. Temporaries differ from variables in that variables come from source language variables that are actually declared, while temporaries are the result of evaluating expressions. Here’s an example:
x = 3 * y >> 2 + sin(5 / y);
(MUL, 3, y, t0) (DIV, 5, y, t1) (SIN, t1, t2) (ADD, 2, t2, t3) (SHR, t0, t3, t4) (COPY, t4, x)
Note how the temporaries are assigned while walking the AST, in a post-order-ish sort of manner:
If Statements
For a typical if-else, generate labels and jumps:
if x > 0 {
print y;
} else {
print y;
}
(JGT, x, 0, L1) (PRINT, x) (JUMP, L2) (LABEL, L1) (PRINT, y) (LABEL, L2)
While Loops
Here is a while loop. We always generate labels at the beginning (for jumping back to the top after a loop body is complete, and also as the target of a continue statement) and the end (in order to escape via a natural end or a break).
while y > 3 {
print y;
y--;
break;
x++;
continue;
x = 1;
}
(LABEL, L1) // always mark top (JLE, y, 3, L2) (PRINT, y) (DEC, y) (JUMP, L2) // break means jump to end (INC, x) (JUMP, L1) // continue means jump to top (COPY, 1, x) (JUMP, L1) // end of while, jump to top (LABEL, L2) // always mark end
Short-Circuit Logic
TODO
Strings
TODO
Arrays
We can make use of relatively powerful tuples to handle arrays:
a[2] = 5; x = a[y * 3]
(ELEM_SET, a, 2, 5) (MUL, y, 3, t0) (ELEM_GET, a, t0, x)
If your arrays are multi-dimensional, we need to find the base-address of a row. This is where ELEM_ADDR comes in:
print a[i][j][k]
(ELEM_ADDR, a, i, t0) (ELEM_ADDR, t0, j, t1) (ELEM_GET, t1, k, t2) (PRINT,t2)
Here’s an example with a for-loop:
for (int i = 0; i < n; i += di)
a[i][j+2] = j;

(COPY, 0, i) // i := 0 (LABEL, L1) // L1: (JGE, i, n, L2) // if i >= n goto L2 (ELEM_ADDR, a, i, t0) // t0 := &a[i] (ADD, j, 2, t1) // t1 := j + 2 (ELEM_SET, j, t0, t1) // t0[t1] := j (IJ, i, di, L1) // i += di, goto L1 (LABEL, L2) // L2:
Structs
A simple example first:
struct Point {
int x; int y;
}
let p: Point;
p.x = 3;
p.y = 4;
print p.y;
(STRUCT_ALLOC, Point, p) (FIELD_SET, p, x, 3) (FIELD_SET, p, y, 4) (FIELD_GET, p, y, t0) (PRINT, t0)
For nested structs, FIELD_ADDR is helpful:
TODO
For fun, here is an example with arrays and structs:
let a: int[];
let a = [32, 16, 8, 4, 2, 1];
a[3] = 21;
let x = a[a[5]];
struct Point {
int x; int y;
}
let polygon: Point[50];
print(polygon[5].y);
(DATA, 32, 16, 8, 4, 2, 1, a) (ELEM_SET, 21, a, 3) (ELEM_GET, a, 5, t0) (ELEM_GET, a, t0, x) (ARRAY_ALLOC, 50, polygon) (ELEM_ADDR, polygon, 5, t2) (FIELD_GET, t2, y, t3) (PRINT, t3)
Subroutines
Let’s start with a simple procedure call:
send(x+5, y, "hello");
(ADD, x, 5, t0) (CALLP, send, t0, y, s0) . . . s0: [104, 101, 108, 108, 111, 0]
Now here is a definition and a call:
func f(i: float): string {
return "dog" unless i >= 3.3;
}
let test: string = f(cos(2.2));
main: (COS, 2.2, t0) (CALLF, f, t0, t1) (COPY, t1, test) (EXIT) f: (JGE, i, 3.3, L0) (RET, s0) L0: (RET) s0: [100, 111, 103]
Here’s an example with recursion:
TODO
Threads
func f() {
for i in 0..<20000 {
print("\(i) ");
}
}
let c1: thread = start f();
let c2: thread = start f();
join(c1);
join(c2);
main: (CALL, __create_thread, f, c1) (CALL, __create_thread, f, c2) (CALL, __join, c1) (CALL, __join, c2) (EXIT) f: (COPY, 0, i) L0: (JGE, i, 20000, L1) (INT_TO_STRING, i, t0) (CALL, __concat_string, s0, t0, t1) (PRINT, t1) (INC_JUMP, i, L0) L1: (RET) s0: [32, 0]
Lower-level Tuples
The tuples we described so far have been quite powerful. They know whether their operands are floats or ints and how big they are. They know the sizes of arrays and structs. They know how much space has been allocated for arrays and automatically do bounds checking if needed.
Eventually, all of this size information will have to appear in machine code. So a good question is where do we start making it explicit. We could take care of all this when we generate assembly language code, or, we can do one more level of IR code generating, using lower level tuples. For example, in this C++ fragment:
double a[20][10];
// ...
for (int i = 0; i < n; i += di)
a[i][j+2] = j;

we have an array of doubles with 20 rows and 10 columns. Doubles are 8 bytes each, so we know each row is 80 bytes. So we know the address of a[0] is the same as the address of a, a[1] is at a+80, a[2] at a+160, and so on. We can do all of the address computations ourselves, avoiding all of the fancy IR tuples, and using only MEM_GET and MEM_SET:
(COPY, 0, i) // i := 0 (LABEL, L1) // L1: (JGE, i, n, L2) // if i >= n goto L2 (MUL, i, 80, t0) // t0 := i * 80 (ADD, a, t0, t1) // t1 := a + t0 (ADD, j, 2, t2) // t2 := j + 2 (MUL, t2, 8, t3) // t3 := t2 * 8 (ADD, t1, t3, t4) // t4 := t1 + t3 (MEM_SET, j, t4) // *t4 := j (ADD, i, di, i) // i := i + di (JUMP, L1) // goto L1 (LABEL, L2) // L2:
TODO - bounds checking? allocation?
Control Flow Graphs
Now that we’ve seen the basics of tuples, let’s see how they are stored and manipulated by a compiler.
A control flow graph is a graph whose nodes are basic blocks and whose edges are transitions between blocks.
A basic block is a:
- maximal-length sequence of instructions that will execute in its entirety
- maximal-length straight-line code block
- maximal-length code block with only one entry and one exit
... in the abscence of hardware faults, interrupts, crashes, threading problems, etc.
To locate basic blocks in flattened code:
- Starts with: (1) target of a branch (label) or (2) the instruction after a conditional branch
- Ends with: (1) a branch or (2) the instruction before the target of a branch.
Here’s an example:
goto L2
L1:
t0 := 3 >> x
t1 := y / t0
x := t1
if y == 0 goto L3
t2 := x - 3
print t2
L3:
L2:
t4 := 4 * y
x := t4 < t5
if t5 != 0 goto L1
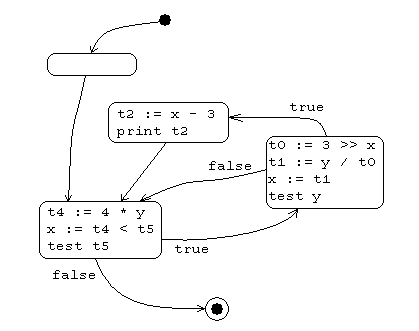
Single Static Assignment
No notes here yet, for now, see Wikipedia.
Generating an IR
In a compiler, you often emit the “first” IR by navigating the CST or the AST and outputting a semantic graph. The graph is a semantically analyzed (decorated) version of the AST. It’s not necessarily a tree because each of the basic entities (variables, functions, types, etc.) may be referenced multiple times.
Writing a Transpiler?If so, you will likely just generate target code directly from the semantic graph. Then you’re done and you don’t have to read on.
But if you are looking to make a more traditional compiler, with machine code as your ultimate goal, read on.
The next level of the IR will be either tuple-based or stack based. You’ll be grouping the tuples into basic blocks for further analysis, but first let’s look at really simple example. To get the idea, here’s a quick-and-dirty illustration of a Haskell program that navigates a semantic graph in a tiny language and outputs an instruction list:
-- A little Compiler from a trivial imperative language to a small
-- single-accumulator machine.
-- Source Language
--
-- Exp = numlit | id | Exp "+" id
-- Bex = Exp "=" id | "not" Bex
-- Com = "skip"
-- | id ":=" Exp
-- | Com ";" Com
-- | "while" Bex "do" Com "end"
data Exp -- Arithmetic Expressions can be
= Lit Int -- literals
| Ident String -- identifiers
| Plus Exp String -- binary plus expressions, left associative
data Bex -- Boolean Expressions can be
= Eq Exp String -- equality comparisons btw exp and identifiers
| Not Bex -- unary not applied to boolean expressions
data Com -- Commands can be
= Skip -- skips (no-ops)
| Assn String Exp -- assignment of an arithmetic expr to an id
| Seq [Com] -- a sequence (list) of commands
| While Bex Com -- a while-command with a boolean condition
-- Target Language
--
-- The target language is an assembly language for a machine with a
-- single accumulator and eight simple instructions.
data Inst
= LDI Int -- Load Immediate
| LD String -- Load
| ST String -- Store
| NOT -- Not
| EQL String -- Equal
| ADD String -- Add
| JMP Int -- Jump
| JZR Int -- Jump if zero
deriving (Show)
-- The Compiler
--
-- ke e loc the code from compiling expression e at address loc
-- kb b loc the code from compiling boolexp b at address loc
-- kc c loc the code from compiling command c at address loc
ke :: Exp -> Int -> [Inst]
ke (Lit n) loc = [LDI n]
ke (Ident x) loc = [LD x]
ke (Plus e x) loc = ke e loc ++ [ADD x]
kb :: Bex -> Int -> [Inst]
kb (Eq e x) loc = ke e loc ++ [EQL x]
kb (Not b) loc = kb b loc ++ [NOT]
kc :: Com -> Int -> [Inst]
kc (Skip) loc = []
kc (Assn x e) loc = ke e loc ++ [ST x]
kc (Seq []) loc = []
kc (Seq (c:cs)) loc =
let f = kc c loc in f ++ kc (Seq cs) (loc + length f)
kc (While b c) loc =
let f1 = kb b loc in
let f2 = kc c (loc + length f1 + 1) in
f1 ++ [JZR (loc + length f1 + 1 + length f2 + 1)] ++ f2 ++ [JMP loc]
-- Pretty-Printing a target program
pprint [] loc = putStrLn ""
pprint (h:t) loc = printInst h loc >> pprint t (loc + 1)
where printInst h loc = putStrLn (show loc ++ "\t" ++ show h)
-- An Example Program
--
-- x := 5;
-- skip;
-- while not 8 = y do
-- z := (19 + x) + y;
-- end;
-- x := z;
prog1 =
Seq [
(Assn "x" (Lit 5)),
Skip,
(While
(Not (Eq (Lit 8) "y"))
(Assn "z" (Plus (Plus (Lit 19) "x") "y"))),
(Assn "x" (Ident "z"))]
-- Top-level call to invoke the Compiler
compile c loc = pprint (kc c loc) loc
-- Since this is just a prototype, run this file as a script
main = compile prog1 0
Here’s the output:
$ runhaskell compiler1.hs 0 LDI 5 1 ST "x" 2 LDI 8 3 EQL "y" 4 NOT 5 JZR 11 6 LDI 19 7 ADD "x" 8 ADD "y" 9 ST "z" 10 JMP 2 11 LD "z" 12 ST "x"
Real-life Examples of IRs
Here are a few things that qualify as intermediate representations, or, at least, things a compiler front-end may output:
- GNU RTL
- The intermediate language for the many source and target languages of the GNU Compiler Collection.
- PCODE
- The intermediate language of early Pascal compilers. Stack based. Responsible for wide adoption of Pascal in the 1970s.
- Java Virtual Machine
- Another virtual machine specification. Almost all Java compilers use this format. So do nearly all Scala, Ceylon, Kotlin, and Groovy compilers. Hundreds of other languages use it as well. JVM code can be interpreted, run on specialized hardware, or jitted.
- Rust Intermediate Languages
- The compiler Rustc transforms source first in to a High-Level Intermediate Language (HIR), then into the Mid-Level Intermediate Language (MIR), then into LLVM. The MIR was introduced in this blog post. You can read more in the original request for it and in the Rustc book.
- CIL
- Common Intermediate Language. Languages in Microsoft’s .NET framework (such as C+, VB.NET, etc.) compile to CIL, which is then assembled into bytecode.
- C
- Why not? It’s widely available and the whole back end is already done within the C compiler.
- C--
- Kind of like using C, but C-- is designed explicitly to be an intermediate language, and even includes a run-time interface to make it easier to do garbage collection and exception handling. Seems to be defunct.
- LLVM
- The new hotness. Much more than just a VM.
- SIL
- The Swift Intermediate Language. Here is a nice presentation on SIL.
- asm.js
- A low-level subset of JavaScript.
- Web Assembly
- An efficient and fast stack-based virtual machine.
A JVM Example
TODO
An LLVM Example
TODO
An SIL Example
TODO
A Web Assembly Example
A C++ function:
unsigned gcd(unsigned x, unsigned y) {
while (x > 0) {
unsigned temp = x;
x = y % x;
y = temp;
}
return y;
}

Compiled to Web Assembly:
(module
(type $type0 (func (param i32 i32) (result i32)))
(table 0 anyfunc)
(memory 1)
(export "memory" memory)
(export "_Z3gcdjj" $func0)
(func $func0 (param $var0 i32) (param $var1 i32) (result i32)
(local $var2 i32)
block $label0
get_local $var0
i32.eqz
br_if $label0
loop $label1
get_local $var1
get_local $var0
tee_local $var2
i32.rem_u
set_local $var0
get_local $var2
set_local $var1
get_local $var0
br_if $label1
end $label1
get_local $var2
return
end $label0
get_local $var1
)
)
Case Study: An IR for C
Guess what? C is such a simple language, an IR is fairly easy to design. Why is C so simple?
- Only base types are several varieties of ints and floats.
- No true arrays —
e1[e2]just abbreviates*(e1+e2); all indicies start at zero, there’s no bounds checking. - All parameters passed by value, and in order.
- Block structure is very restricted: all functions on same level (no nesting); variables are either truly global or local to a top-level function; implementation drastically simplified because no static links are ever needed and functions can be easily passed as parameters without scoping trouble.
- Structure copy is bitwise.
- Arrays aren’t copied element by element: array assignment is just an assignment of the starting address.
- Language is small; nearly everything interesting (like I/O) is in a library. So we only need tuples for the core language.
The tuples already given are more than sufficient to use in a C compiler.
Summary
We’ve covered:
- ...
- ...