k-ary Trees
Definition
A $k$-ary tree is a tree in which the children of a node appear at distinct index positions in $0 \ldots k-1$. As a consequence, the maximum number of children for a node is $k$.
Some $k$-ary trees have special names
- 2-ary trees are called binary trees.
- 3-ary trees are called trinary trees or ternary trees.
- 1-ary trees are called lists.
You have to draw $k$-ary trees carefully. The index position of every node is an inherent part of a $k$-ary tree. In a binary tree, for example, if a node has one child, you can't draw a vertical line from the parent to the child. Every child in a binary tree is either a left or a right child; that must be made clear.
Representations
Since the subtrees of a node are both indexed and bounded, we can use an array for them. Here is an example for a $4$-ary tree:
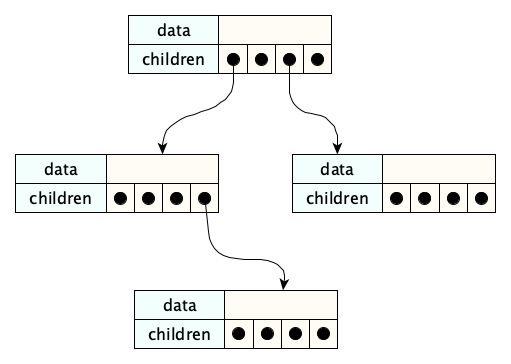
Here’s something cool. You can also use a single array for the whole tree! For example, in a $3$-ary tree, there is one root node, three nodes on the next level, nine on the next, and so on. You assign indexes top-to-bottom, left-to-right, in the following (hopefully intuitive) manner:
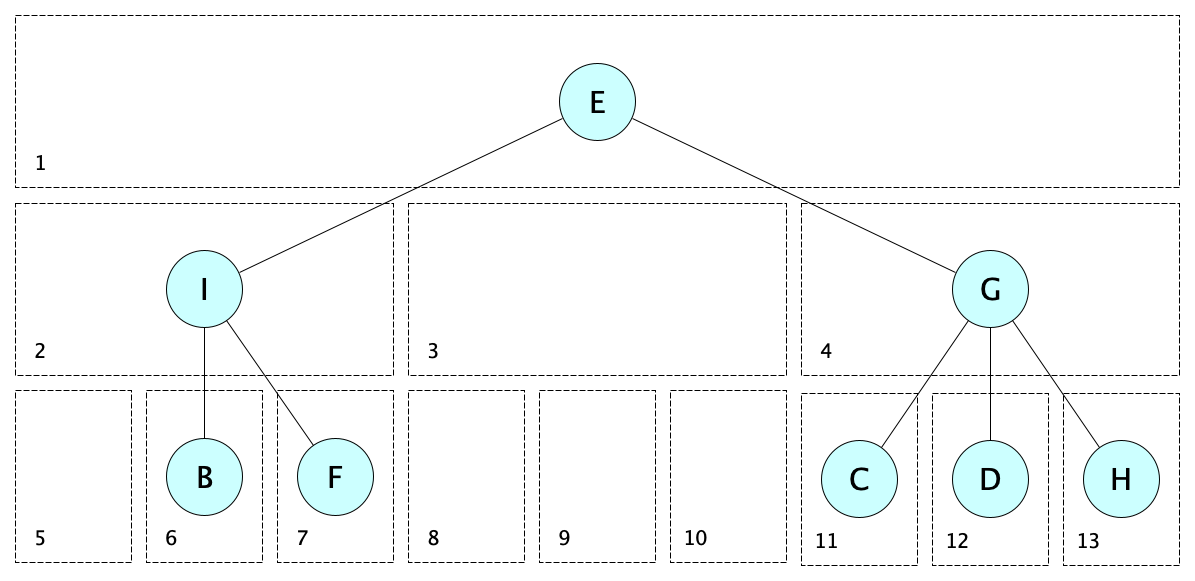
This tree is stored in an array as follows:
┌───────┐
1 │ E │
├───────┤
2 │ I │
├───────┤
3 │ │
├───────┤
4 │ G │
├───────┤
5 │ │
├───────┤
6 │ B │
├───────┤
7 │ F │
├───────┤
8 │ │
├───────┤
9 │ │
├───────┤
10 │ │
├───────┤
11 │ C │
├───────┤
12 │ D │
├───────┤
13 │ H │
└───────┘
For ease of “navigation” through a tree represented this way, we store the root at index position 1. This makes it easy to compute the indices of parents and children. In a binary tree:
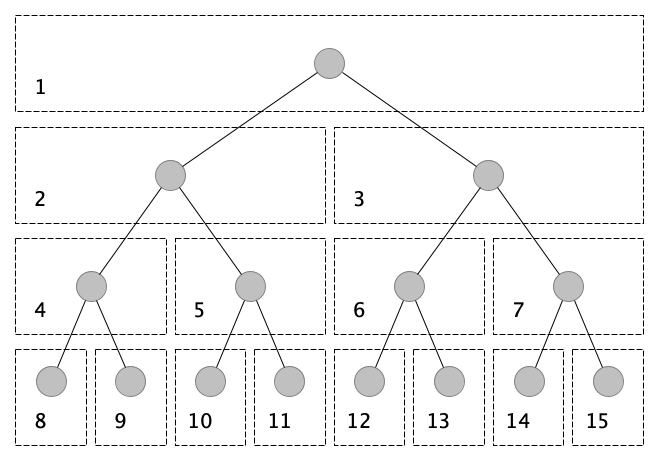
the indexing is not too difficult to derive. It’s just:
- Parent($i$) = $\lfloor \frac{i}{2}\rfloor$
- LeftChild($i$) = $2i$
- RightChild($i$) = $2i + 1$
In general, for arbitrary $k$, yeah, it’s a bit messier, but you can write the code once and tuck it way inside a convenient method:
- Parent($i$) = $\frac{k + i - 2}{k}$
- $j$th child of $i$ = $ki - (k - 2) + j$
Complete Trees
The array representation may waste a lot of space, especially when the tree is sparse. The maximally space efficient $k$-ary tree is called a complete tree. A complete tree is completely filled out on every level, except perhaps on the last one, on which all we require is that all its nodes are “as far to the left as possible.”
Complete trees can be packed into an array with no wasted space at all.
Draw some complete trees.
Applications of Complete TreesThe complete binary tree is the structure underlying the powerful priority queue representation known as the heap. Priority queues are among the most useful types in computer science, and the heap structure provides an extremely efficient representation.
Perfect Trees
A perfect k-tree is a $k$-ary tree in which every node is either a $0$-node or a $k$-node and all leaves are on the same level.
Perfect trees are sometimes called full trees, though some people say a full tree is just one in which every node is a $0$-node or a $k$-node, without caring whether all leaves are on the same level or not.
The Size of $k$-ary Trees
As computer scientists, you will want to build up an intuition for just how many nodes a $k$-ary tree can pack into a certain number of levels, and how many nodes there can be on each level, and how many nodes there can be on the last level versus the nodes above it. For many people, the answers to these questions go against one’s intuition and can be quite surprising. They also provide a foundation for some truly fascinating algorithms (like iterative deepening search) you will learn about later.
For now, let’s hone our mathematical skills and work out answers to these questions, somewhat slowly at first, building up to general formulas, then applying them to see if indeed the numbers lead us to anything interesting. We start with $k = 2$:
| Level | #Nodes on this level |
Total #Nodes on all levels above this one |
Total #Nodes on all levels above and including this one |
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 1 | 2 | 1 | 3 |
| 2 | 4 | 3 | 7 |
| 3 | 8 | 7 | 15 |
| 4 | 16 | 15 | 31 |
| 5 | 32 | 31 | 63 |
| 6 | 64 | 63 | 127 |
| 7 | 128 | 127 | 255 |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $h$ | $2^h$ | $2^h-1$ | $2^{h+1}-1$ |
Notice the exponential growth of the number of nodes relative to the height of the tree.
IMPORTANT OBSERVATION: In any full binary tree, more than half the nodes are on the last level! Note how a tree with 7 levels has 127 nodes in all of the first six levels, but 128 on the last level. Again: there are more nodes on the last level alone than there total in ALL the levels above.
- 1267650600228229401496703205376 nodes on the bottom level.
- 1267650600228229401496703205375 nodes total over all of the first 99 levels.
Okay so we got a sense of size for binary trees. What about arbitrary $k$-ary trees?
We can see (clearly, hopefully) that the number of nodes on level $h$ is $k^h$. Let’s try to get the total number of nodes for a perfect tree of height $h$. Let $S(h)$ be that number. Let’s try to get a closed-form solution for it.
$S(h) = 1 + k + k^2 + k^3 + ... + k^h$
$k \times S(h) = k + k^2 + k^3 + k^4 + ... + k^{h+1}$
$k \times S(h) - S(h) = k^{h+1}-1$
$(k-1) \times S(h) = k^{h+1}-1$
$\boxed{S(h) = \frac{k^{h+1}-1}{k-1}}$
Now let’s get a sense of growth:
| Height | Number of Nodes in Perfect $k$-ary Tree where $k =$ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Trees get big, pretty fast, right?
Let’s revisit that “There are more nodes on the last level alone than among all levels above the last one” truth. Here is a 5-ary tree:
There are 125 nodes on the fourth level, but totalling up all the nodes on the first three levels, there are only 41. So there are over three times as many nodes on the last level as there are nodes in the rest of the tree. When trees have a large $k$, the vast majority of the nodes are on the last level.
Why should I care?This phenomenon is the basis of the powerful search technique of iterative deepening, which you will learn about in courses in Algorithms or Artificial Intelligence.
Summary
We’ve covered:
- What an ordered tree is
- How k-ary trees can be represented, with links
- How k-ary trees can be represented in arrays
- Perfect Trees
- Complete k-ary Trees, and why they matter
- The exponential nature of the size of k-ary trees