Solving the Kirkman Schoolgirl Problem
The Problem
In 1850, when it was more common than today for kids to walk to school in large groups, Thomas Kirkman posed this problem:
Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily so that no two shall walk twice abreast.
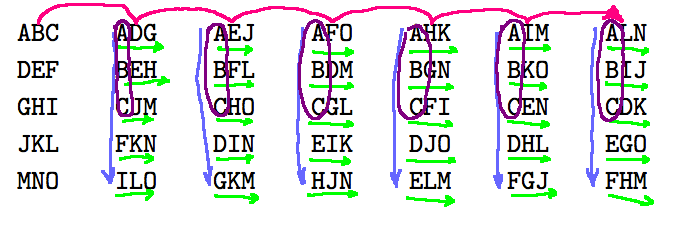
Say the girls are named Ani, Bhekisisa, Ciara, Dora, Eimi, Francesca, Galina, Henrietta, Imogen, Jia, Kameke, Luiza, Menna, Nazila, and Olivia. Here's one solution:
| Sun | Mon | Tue | Wed | Thu | Fri | Sat |
|---|---|---|---|---|---|---|
| ABC DEF GHI JKL MNO | ADG BEH CJM FKN ILO | AEJ BFL CHO DIN GKM | AFO BDM CGL EIK HJN | AHK BGN CFI DJO ELM | AIM BKO CEN DHL FGJ | ALN BIJ CDK EGO FHM |
Why Is It Interesting?
To solve this problem, you can’t just take the naïve approach of generating all the possible arrangments one by one, checking each one to see it if meets the problem constraints. There are $15!$ ways the walkers can arrange themselves in a day and there are $(15!)^{7}$ ways to pick seven daily arrangements. That's actually a big number.
$(15!)^{7}=$ 6,538,788,315,119,179,526,047,380,411,895,480,779,825,576,867,866,060,412,873,080,832,000,000,000,000,000,000,000.
We can lock down the first permuation, so we only have to figure out six more:
That helped a little. $(15!)^{6}=$ 5,000,318,485,342,659,500,723,180,353,639,447,324,416,453,552,346,497,024,000,000,000,000,000,000
But we can do better. After the first day, we can put the first three walkers
in fixed places, leaving us to find six permuations of the other 12 walkers:
$(12!)^{6}=$ 12,078,744,213,598,964,456,884,373,878,200,091,017,216,000,000,000,000.
Still a big number. Even if we had a billion supercomputers working side-by-side, each generating and checking a trillion configurations per second, it would still take over $3.8 \times 10^{23}$ years to examine all solutions. That's about 28 trillion times the age of the universe.
So we have to do better.
Because we care only that each walker walks in a row with every other walker over the seven days, many solutions are actually isomorphic to each other: shuffling walkers within a row, shuffling rows within a day, and shuffling days within the week don't fundamentally change a solution. We can therefore identify the most basic arrangement within a class of isomorphic solutions as one having the following constraints: A consequence of these sorting constraints is that:
By using only these five constraints, we can find a backtracking solution with less than 200 million trial placements of walkers in different positions, which takes only a couple seconds on a typical computer. You may have seen the problem solving paradigm known as backtracking, in which rather than generating and testing complete arrangments, we can build up solutions in a systematic way, checking whether “partial solutions” have any chance of becoming a complete solution. The following is a little animation of how a single solution can be found. It runs quite slowly by design, to give you the opportunity to see the computation carried out. Try it.
Checks: 0 In a backtracking implementation, each of the 105 slots are filled with one of the walkers A...O. As a first pass, without any constraints, you would build the backtracking engine of a script as follows:
and kick off the program with:
To speed things up, we should be careful which walkers we try to place in a given slot. We don’t always need to try each of the walkers A...0. We should figure out how to make this range smaller, say start...end, for some subrange. How can we determine this smaller range? This gives us: The simple backtracking algorithm above results in: I created several different implemenations of this algorithm, and ran them
on a 2015-era MacBook Pro laptop. Here's what I've managed so far: The timings were made by running the program several times under the command line
Note that for C, Rust, and Go I pre-compiled the application and only
timed the executable. For each of the other languages, the total time will include
compilation and the start up of the virtual machine. Well, in Java's case
I found that timing the code inside the script improved its numbers a lot, so
that's what I did. I should do the same for Julia, because it is known to
have a slow startup time. If I did the same for Node, JavaScript might actually
be faster than Java. Who knows. I can get to that stuff later. Note: In each of the implementations, the number
of rows and columns were script parameters and experiments were done
with the values set to 5 and 3. All constraint checks used parameters, never
hard-coded values, so yes, the code could have been shorter and faster. We can immediately generate a solution from this cool little animation made by String, based off work by Reinhard Laue:
The diagram shows the 15 walkers grouped into 5 rows of three. The walkers for the next day are found by “rotating” the groups. I’ve numbered them like so:
Here’s a Ruby program to generate the walkers for the seven days:
You can code golf it (down to 86 characters) and execute it directly on the command line to impress your friends:
The above output means that on the first day, walkers 0, 2, and 9 are in the first row; walkers 3, 7, and 8 are in the second row; 4, 5, and 14 in the third row; 6, 1, and 12 in the fourth; and 10, 11, and 13 are in the last row. We can add a little more code to get a more graphical output. Let’s golf that, too:
Here is a JavaScript solution:
It is possible to use tools such as SAT Solvers and Inference Engines (such as
the Prolog Programming Language) to solve the problem. TODO TODO It turns out that there are actually seven distinct (non-isomorphic) solutions.
And I haven't bothered to even look for all of them. One was enough for me. Kirkman
found them all back in the 1850s. Others have found them all as well; you'll have
to consult their work to see how they found them. For more background on the problem, some papers, and other people's solutions, see:
ABC ... ... ... ... ... ...
DEF ... ... ... ... ... ...
GHI ... ... ... ... ... ...
JKL ... ... ... ... ... ...
MNO ... ... ... ... ... ...
ABC A.. A.. A.. A.. A.. A..
DEF B.. B.. B.. B.. B.. B..
GHI C.. C.. C.. C.. C.. C..
JKL ... ... ... ... ... ...
MNO ... ... ... ... ... ...
Constraints
Backtracking
Structuring a Backtracking Solution
def place_from(slot):
for walker in 'A'..'O':
if can_walk(slot, walker):
place_walker(slot, walker)
if slot == LAST_SLOT:
finish()
else:
place_from(slot+1)
place_from(0)
Implementing Constraint Checking during Backtracking
def place_from(slot):
start = determine_first_walker_to_test(slot)
end = determine_last_walker_to_test(slot)
for walker in start..end:
if can_walk(slot, walker):
place_walker(slot, walker)
if slot == LAST_SLOT:
finish()
else:
place_from(slot+1)
Some Results
place_from
Language Compiler Time Notes
C Apple LLVM version 9.1.0 (clang-902.0.39.1) 1.324 sec -O3
Rust rustc 1.25.0 1.352 sec rustc -C opt-level=3 -C lto -C target-cpu=native
Go go version go1.10.1 darwin/amd64 1.796 sec
Java Version 1.8.0_66 Java HotSpot(TM) 64-Bit Server VM (build 25.66-b17, mixed mode) 2.322 sec
JavaScript Node.js v9.5.0 2.542 sec
Swift Apple Swift version 4.1 (swiftlang-902.0.48 clang-902.0.37.1) 3.359 sec -Ounchecked
Julia Julia 0.4.0-rc2 release x86_64-apple-darwin13.4.0 9.569 sec -O --check-bounds=no
Python
(PyPy)Python 3.5.3 PyPy 6.0.0 with GCC 4.2.1 Compatible Apple LLVM 9.1.0 (clang-902.0.39.1) 13.784 sec
Lua Lua 5.3.1 Copyright (C) 1994-2015 Lua.org, PUC-Rio 47.19 sec I wonder how much better LuaJIT will be
Python
(Cython)Python 3.6.4 (default, Mar 1 2018, 18:36:50)
[GCC 4.2.1 Compatible Apple LLVM 9.0.0 (clang-900.0.39.2)] on darwin 129.5 sec
time command and taking the smallest user time. I did not
include real or sys times because user time matters most
here. Exception: Julia automatically used multiple cores so the real
time was less than the user time, so I used real time for it.Analytic Solutions
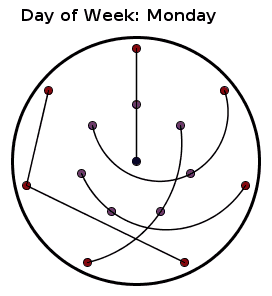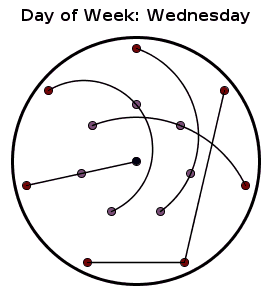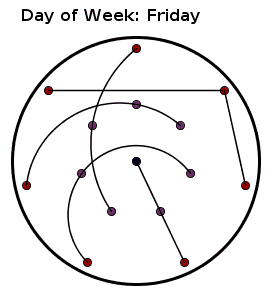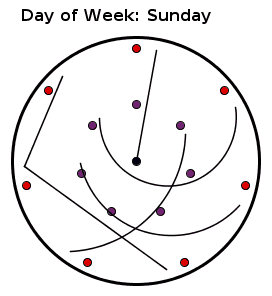
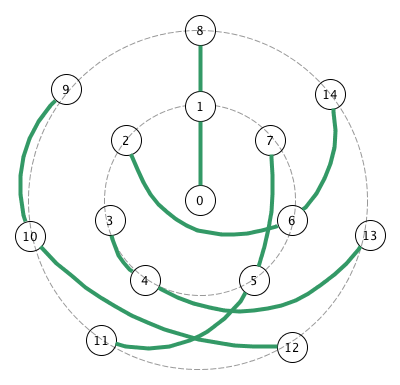
s = [0, 1, 8, 2, 6, 14, 3, 4, 13, 5, 7, 11, 9, 10, 12]
7.times {p s.map! {|x| x==0 ? 0 : x==14 ? 8 : x==7 ? 1 : x+1}}
$ ruby -e 's=[0,1,8,2,6,14,3,4,13,5,7,11,9,10,12];7.times{p s.map!{|x|x==0?0:x==14?8:x==7?1:x+1}}'
[0, 2, 9, 3, 7, 8, 4, 5, 14, 6, 1, 12, 10, 11, 13]
[0, 3, 10, 4, 1, 9, 5, 6, 8, 7, 2, 13, 11, 12, 14]
[0, 4, 11, 5, 2, 10, 6, 7, 9, 1, 3, 14, 12, 13, 8]
[0, 5, 12, 6, 3, 11, 7, 1, 10, 2, 4, 8, 13, 14, 9]
[0, 6, 13, 7, 4, 12, 1, 2, 11, 3, 5, 9, 14, 8, 10]
[0, 7, 14, 1, 5, 13, 2, 3, 12, 4, 6, 10, 8, 9, 11]
[0, 1, 8, 2, 6, 14, 3, 4, 13, 5, 7, 11, 9, 10, 12]
$ ruby -e 's=[0,1,8,2,6,14,3,4,13,5,7,11,9,10,12]
7.times{s.map!{|x|x==0?0:x==14?8:x==7?1:x+1}.each_slice(3){|r|
puts r.map{|g|(g+65).chr}.join()};puts}'
ACJ
DHI
EFO
GBM
KLN
ADK
EBJ
FGI
HCN
LMO
AEL
FCK
GHJ
BDO
MNI
AFM
GDL
HBK
CEI
NOJ
AGN
HEM
BCL
DFJ
OIK
AHO
BFN
CDM
EGK
IJL
ABI
CGO
DEN
FHL
JKM
s=[0,1,8,2,6,14,3,4,13,5,7,11,9,10,12]
for(i=0;i<7;i++)console.log(s=s.map(x=>!x?0:x<8?x%7+1:x%7+8))
Constraint-Based Solutions
Heuristics
Finding All Solutions
More Information