Numeric Encoding

Numbers and Numerals
A number is an abstraction of quantity. Humans started with counting numbers like one, two, three, four and so on. Zero came later. Then someone realized that subtracting six from two could be useful and so invented negative numbers. Then integer division led to the creation of rational numbers, and other work resulted in irrational numbers, real numbers, transfinite numbers, imaginary numbers, complex numbers and so on.
A number is represented by a numeral.
Egyptian Numerals
Egyptians wrote numerals in hieroglyphs for thousands of years; here are the important symbols and their numeric values:
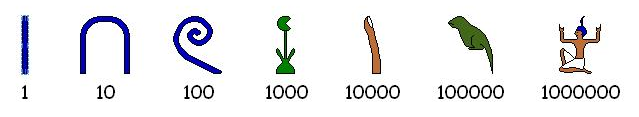
Notice that these numerals could be written from right-to-left or left-to-right or vertically or a combination of vertical and horizontal. Here is one way to represent twenty-one thousand two hundred thirty-seven:
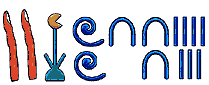
We don’t use these numerals in computer systems today, but history is important, so please read more about these numerals at Wikipedia or elsewhere.
Roman Numerals
Well, these aren’t much use in modern computers, either. Enough said. Besides, they’re really hard to understand, and they don’t have a zero, or wait...maybe they do?
Positional Numeral Systems
A Positional Numeral System has an ordered set of digits that includes 0 as its first member. The number of digits in the set is called the base. By far the most common of these is the Hindu-Arabic Numeral System, or Arabic Numeral System, which has a base of 10, and whose glyphs are these:
0 1 2 3 4 5 6 7 8 9
There are other positional systems, too:
- Devanagari (base 10): ० १ २ ३ ४ ५ ६ ७ ८ ९
- Mongolian (base 10): ᠐ ᠑ ᠒ ᠓ ᠔ ᠕ ᠖ ᠗ ᠘ ᠙
- Kannada (base 10): ೦ ೧ ೨ ೩ ೪ ೫ ೬ ೭ ೮ ೯
- Tamil (base 10): ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯
- Maya (base 20)
- Kaktovik Iñupiaq (base 20)
Kaktovik numerals are awesome:

So are the Cistercian numerals.
Want to see more? Check out Ian Taylor’s Unicode Numerals page.
In computing, though, the Hindu-Arabic numerals dominate. We can extend this system to bases other than 10 by adding or removing glyphs. Bases up to 36 are traditionally handled by adding the Latin letters A-Z. The most common systems in computing are:
- Decimal: digit set =
{0,1,2,3,4,5,6,7,8,9}, base = 10. - Octal: digit set =
{0,1,2,3,4,5,6,7}, base = 8. - Hexadecimal: digit set =
{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, base = 16. - Binary: digit set =
{0,1}, base = 2.
You generate positional numerals starting at 0 by a really easy algorithm you already know.
| Decimal | Octal | Hex | Binary |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 10 | 8 | 1000 |
| 9 | 11 | 9 | 1001 |
| 10 | 12 | A | 1010 |
| 11 | 13 | B | 1011 |
| 12 | 14 | C | 1100 |
| 13 | 15 | D | 1101 |
| 14 | 16 | E | 1110 |
| 15 | 17 | F | 1111 |
| 16 | 20 | 10 | 10000 |
| 17 | 21 | 11 | 10001 |
| 18 | 22 | 12 | 10010 |
| 19 | 23 | 13 | 10011 |
| 20 | 24 | 14 | 10100 |
| 21 | 25 | 15 | 10101 |
| 22 | 26 | 16 | 10110 |
| 23 | 27 | 17 | 10111 |
| 24 | 30 | 18 | 11000 |
| 25 | 31 | 19 | 11001 |
| 26 | 32 | 1A | 11010 |
| 27 | 33 | 1B | 11011 |
| 28 | 34 | 1C | 11100 |
| 29 | 35 | 1D | 11101 |
| 30 | 36 | 1E | 11110 |
| 31 | 37 | 1F | 11111 |
| 32 | 40 | 20 | 100000 |
| 33 | 41 | 21 | 100001 |
| ... | ... | ... | ... |
Third Graders, Binary Numbers, and the Socratic Method
For some inspiration, read about a third grade class’s adventures in learning about and using binary numerals.
Conversion
Let’s convert Hex to and from Binary. Wait, this is trivial. Each group of four bits maps exactly to one hex digit. MEMORIZE THIS MAPPING SO YOU CAN DO THE CONVERSION BY SIGHT. Examples:
48C = 0100 1000 1100 CAFE54 = 1100 1010 1111 1110 0101 0100
Hex to Decimal: All Arabic numeral systems use place values which you should already be aware of. Examples:
E2A = 14(162) + 2(161) + 10(160)
= 14(256) + 2(16) + 10
= 3626
For numbers involving only two hex-digits you can do this in your head if you have memorized your multiples of 16: 0→0, 1→16, 2→32, 3→48, 4→64, 5→80, 6→96, 7→112, ... F→240. This gives you the contribution of the first hex digit, so just “add in” the second.
Decimal to Hex: Keep on dividing by 16, working your way backwards. Example:
3653
/ \
228 5
/ \
14 4
/ \
0 14
==> E45
Binary to Decimal: Read left-to-right, doubling as you go and adding one where necessary. Example:
10110110
Say “1, 2, 5, 11, 22, 45, 91, 182.” Very easy! Of course, once you’re a pro you might just say “176 + 6 = 182” because you immediately see the 8 bits as a 1011 and a 0110, i.e., an 11 and a 6, and 16×11 is 176, etc.
This method is, in some circles, known as Dorin’s Way.
What about conversion between arbitrary bases? Well, it’s pretty cool to know how to generic conversions, but our focus today is strictly on binary, hex, and decimal.
Addition
You learned the addition method a long time ago for decimal numerals; the same idea applies to other bases.
Examples in Binary
11010 101111 001 01 01101 111101 111 00 100111 1101100 1000 01
Examples in Hex
D371 9 37EE 89CA 26A2 9 F0 CC18 FA13 12 38DE 155E2
Subtraction, Multiplication, and Division
You probably learned algorithms for these operations, long ago; the good news is that they are base-independent. Try some of these out in binary: you'll find they're quite simple, though they might take longer since there are so many bits, even for small quantities.
Fixed Bit-Length Integers
Computers have storage locations with a fixed number of bits. The bits are numbered starting at the right. Examples:
| 3 | 2 | 1 | 0 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
Storage locations come in many sizes. Usually we write the values in a storage location out in hex; the contents of our above examples are C, A7, and 3F25, respectively.
An $n$-bit storage location can store $2^n$ distinct bit strings so it can encode (“unsigned”) integers from 0 through $2^n-1$. If we want to include some negative numbers (“signed”) we have several encoding options, but by far the most common is called the Two’s complement representation, which allocates the bit strings to the numbers $-2^{n-1}$ through $2^{n-1}-1$. Please note that a given bit string can be interpreted as either an unsigned number or a signed one.
Here’s how things look in a four-bit storage location, with signed values using the two’s complement representation:
| Binary | Hex | Unsigned Decimal | Signed Decimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 8 | 8 | -8 |
| 1001 | 9 | 9 | -7 |
| 1010 | A | 10 | -6 |
| 1011 | B | 11 | -5 |
| 1100 | C | 12 | -4 |
| 1101 | D | 13 | -3 |
| 1110 | E | 14 | -2 |
| 1111 | F | 15 | -1 |
For 32-bit locations there are 4294967296 possible bit strings; here are some of them:
| Binary | Hex | Unsigned Decimal | Signed Decimal |
|---|---|---|---|
| 00000000000000000000000000000000 | 00000000 | 0 | 0 |
| 00000000000000000000000000000001 | 00000001 | 1 | 1 |
| ... | ... | ... | ... |
| 01101000101011111110000100001101 | 68AFE10D | 1756356877 | 1756356877 |
| ... | ... | ... | ... |
| 01111111111111111111111111111110 | 7FFFFFFE | 2147483646 | 2147483646 |
| 01111111111111111111111111111111 | 7FFFFFFF | 2147483647 | 2147483647 |
| 10000000000000000000000000000000 | 80000000 | 2147483648 | -2147483648 |
| 10000000000000000000000000000001 | 80000001 | 2147483649 | -2147483647 |
| ... | ... | ... | ... |
| 10010111010100000001111011110011 | 97501EF3 | 2538610419 | -1756356877 |
| ... | ... | ... | ... |
| 11111111111111111111111111111110 | FFFFFFFE | 4294967294 | -2 |
| 11111111111111111111111111111111 | FFFFFFFF | 4294967295 | -1 |
Here are the values that can represented in locations of different sizes:
| Bits | Unsigned Range | Signed Range |
|---|---|---|
| 8 | 00…FF 0…255 | 80…7F -128 …127 |
| 16 | 0000…FFFF 0 …65,535 | 8000…7FFF -32,768 …32,767 |
| 24 | 000000…FFFFFF 0…16,777,215 | 800000…7FFFFF -8,388,608…8,388,607 |
| 32 | 00000000…FFFFFFFF 0…4,294,967,295 | 80000000…7FFFFFFF -2,147,483,648…2,147,483,647 |
| 64 | 0000000000000000…FFFFFFFFFFFFFFFF 0…18,446,744,073,709,551,615 | 8000000000000000…7FFFFFFFFFFFFFFF -9,223,372,036,854,775,808 …9,223,372,036,854,775,807 |
Fixed-Length Integer Addition
When adding numbers using fixed length storage locations, the sum might not fit. This is called overflow.
Example: 8-bit location, unsigned numbers. Add C5 + EE. The value should be 1B3, but that won’t fit! Why? (Note: in decimal, this is adding 197 + 238 = 435, which is outside the range of 0..255.)
Saturated vs. Modular Addition
There are two main approaches to dealing the problem of a sum not being able to fit. We could:
- Clamp the sum at the maximum representable value. This is called saturated arithmetic. In the previous example the sum would be FF (or 255 decimal).
- Ignore the carry, making our example’s result as B3. This is called modular (or wraparound) arithmetic.
What about signed numbers? Example: Try 6C + 53. You get 6C + 53 = BF. Well, you didn’t carry anything out when you added, and the answer still fits in 8 bits, but you added two positive numbers and got a negative result. This too, is overflow. Again we could:
- Clamp the sum at the maximum representable value (which in the above example is 7F).
- Leave the result as BF.
Almost all computers do modular arithmetic. Some do modular and saturated arithmetic. For example, in the Intel x86 family, modular addition is done with the add or padd instructions, and saturated addition is done with padds or paddus instructions.
Overflow Detection
You have to know how to detect overflow. For unsigned numbers this occurs precisely when you carry out of the highest order bit. For signed numbers this occurs precisely when you’ve added two positive numbers and got a negative result, or added two negative numbers and got a positive result.
Examples of signed modular addition in 8-bit storage locations:
2C 78 42 E0 87 FF
38 6A FC 75 DA C1
64 E2 3E 55 61 C0
~C ~C C C C C
~O O ~O ~O O ~O
Subtraction for fixed-length Integers
Because of the cool way the two’s complement representation works, you can subtract a-b by computing a+(-b). So just find the additive inverse of b and add it to a. By the way someone with a really sick sense of humor called the additive inverse the two’s complement and the name stuck. Finding the additive inverse is easy: just invert every bit and add 1!
Hold on! Before you start doing this, make sure you understand why this is correct.
Example in 8 bits: 44 decimal is 2C in hex or 00101100 in binary. So -44 decimal is found like this:
00101100 =====invert bits=====> 11010011
1
add 1 --------
11010100 ==> D4
So this says that 2C and D4 are inverses. To do a sanity check, add them together and make sure you get zero. Check: 2C+D4=00.
A subtraction example in 8 bits:
E2-83 = E2+(-83) = E2+7D = 5F
By the way, if you start “thinking in hex”, you can do this stuff much faster. We’ll see better techniques in class.
Prefix Multipliers for Sizes in Bytes
When numbers get really large you can use some special values:
| Tens | Twos | ||||||
|---|---|---|---|---|---|---|---|
| k | kilo | 103 | Thousand | Ki | kibi | 210 | 1,024 |
| M | mega | 106 | Million | Mi | mebi | 220 | 1,048,576 |
| G | giga | 109 | Billion | Gi | gibi | 230 | 1,073,741,824 |
| T | tera | 1012 | Trillion | Ti | tebi | 240 | 1,099,511,627,776 |
| P | peta | 1015 | Quadrillion | Pi | pebi | 250 | 1,125,899,906,842,624 |
| E | exa | 1018 | Quintillion | Ei | exbi | 260 | 1,152,921,504,606,846,976 |
| Z | zetta | 1021 | Sextillion | Zi | zebi | 270 | 1,180,591,620,717,411,303,424 |
| Y | yotta | 1024 | Septillion | Yi | yobi | 280 | 1,208,925,819,614,629,174,706,176 |
| R | ronna | 1027 | Octillion | Ri | robi | 290 | 1,237,940,039,285,380,274,899,124,224 |
| Q | quetta | 1030 | Nonillion | Qi | quebi | 2100 | 1,267,650,600,228,229,401,496,703,205,376 |
As of 2023, robi and quebi are unofficial names.
Beyond quetta?
Nothing is official yet, but there are a few places on the web (such as this one by René Nyffenegger) where folks have speculated on future prefixes. You’ll find funny ones like vunda, sorta, and nena, and minga. Oh well.
4 Ki = 22210 = 212 = 4096 64 Ki = 26210 = 216 = 65536 256 Ki = 28210 = 218 = 262144 16 Mi = 24220 = 224 = 16777216 4 Gi = 22230 = 232 = 4294967296 32 Ti = 25240 = 245 = 35184372088832 2 Pi = 21250 = 251 = 2251799813685248 1 EiB is 1024 PiB.
Real Numbers
A real number is, well, I leave it to you to look up its formal mathematical definition because it isn’t really trivial. But you should have some idea. The important thing here is: how can we represent them in fixed-length storage locations? We could use integer pairs for numbers we know to be rational, or take a long string and assume the decimal point is always in a certain place (called a fixed-point representation), or use a floating-point representation.
Floating Point Encodings
Most modern general purpose computers use an encoding scheme for floating point values called IEEE 754. There are several encodings within this standard. The two most popular are binary32 and binary64.
IEEE 754 binary32
The thirty-two bits are broken into three sections, the sign ($s$), the fraction ($f$), and the exponent ($e$).
| 31 | 30 | 23 | 22 | 0 |
| s | e | f | ||
Taking $s$, $f$, and $e$ as unsigned values, the value of the number, in decimal, is:
| e | f | s | value |
|---|---|---|---|
| 1..254 | anything | 0 | $(1+f\times 2^{-23})\times 2^{e-127}$ |
| 1 | $-(1+f\times 2^{-23})\times 2^{e-127}$ | ||
| 0 | 0 | 0 | $+0$ |
| 1 | $-0$ | ||
| not 0 | 0 | $(f\times 2^{-23})\times 2^{-126}$ | |
| 1 | $-(f\times 2^{-23})\times 2^{-126}$ | ||
| 255 | 0 | 0 | $+\infty$ |
| 1 | $-\infty$ | ||
| 1...222-1 | anything | Signaling NaN | |
| 222...223-1 | Quiet NaN |
Example: What does C28A8000 represent? In binary, it is:
1 10000101 00010101000000000000000
So, s = 1, e = 133. Our value is then -(1.00010101)2 × 26 = -(1000101.01)2 which is clearly -69.25 in decimal.
IEEE 754 binary64
The sixty-four bits are broken into three sections, the sign ($s$), the fraction ($f$), and the exponent ($e$):
| 63 | 62 | 52 | 51 | 0 |
| s | e | f | ||
Taking $s$, $f$, and $e$ as unsigned values, the value of the number, in decimal, is:
| e | f | s | value |
|---|---|---|---|
| 1..2046 | anything | 0 | (1 + f × 2-52) × 2e-1023 |
| 1 | -(1 + f × 2-52) × 2e-1023 | ||
| 0 | 0 | 0 | +0 |
| 1 | -0 | ||
| not 0 | 0 | (f × 2-52) × 2-1022 | |
| 1 | -(f × 2-52) × 2-1022 | ||
| 2047 | 0 | 0 | +infinity |
| 1 | -infinity | ||
| 1...251-1 | anything | Signaling NaN | |
| 251...252-1 | Quiet NaN |
Special Floating Point Values
NaN means “not a number.” Quiet NaNs (QNaNs) propagate happily through computations. Signaling NaNs (SNaNs) can be used to signal serious problems. You can use them to indicate uninitialized variables, for example.
- Overflowing addition, subtraction, multiplication gives the expected infinity
- Adding two positive infinities gives positive infinity
- Adding two negative infinities gives negative infinity
- But infinity minus infinity = NaN
- A finite value divided by an infinity = 0
- Any nonzero value divided by 0 = infinity
- But 0 / 0 = NaN
- infinity × 0 = NaN
- infinity × infinity = infinity
- infinity / infinity = NaN
- Any arithmetic operation on a NaN results in NaN
- A NaN never compares equal to anything, not even another NaN
Other Formats
The IEEE 754 Standard also includes:
- binary16: 1 sign bit, 5 exponent bits, 10 fraction bits
- binary128: 1 sign bit, 15 exponent bits, 112 fraction bits
- binary256: 1 sign bit, 19 exponent bits, 236 fraction bits
- decimal32, decimal64, and decimal28
Other formats of interest:
More Information
Here’s Tom Scott explaining floating point:
If you would like to see a more extensive summary of IEEE 754, see Steve Hollasch’s. It is quite good. Oh, and you should read Goldberg’s classic paper.
If you would like to experiment with online IEEE 754 converters, you can use mine (which is okay), or the one at City University of New York, which is awesome.
Summary
We’ve covered:
- Number vs. numeral
- Egyptian numerals
- Positional numeral systems
- Fixed-length integer encodings
- Floating-point encodings
- IEEE 754 binary32 and binary64