Programming Language Specification
Let’s Design a Language
Let’s consider the language of infix integer arithmetic expressions with optional parentheses, the operators plus, minus, times, divide, and unary negation, and with spaces and tabs allowed between numbers and operators. We’ll call the language Ael, for Arithmetic Expression Language.
Getting Started
When designing a language, it’s a good idea to start by sketching forms that you want to appear in your language as well as forms you do not want to appear.
| Examples | Non-Examples |
|---|---|
432 24* (31/899 +3-0)/(54 /2+ 4+2*3) (2) 8*(((3-6))) |
43 2 24*(31/// /)/(5+---+)) [fwe]23re 3 1 124efr$#%^@ --2-- |
Concrete Syntax
Next, we look at the legal forms, and create a grammar for the concrete syntax. Here is our first try (it will turn out to not be very good, but it works):
For consistency, we’ll be using Ohm notation throughout this course, unless a different notation is specifically noted.
exp = space* exp space* op space* exp space*
| space* numlit space*
| space* "-" space* exp space*
| space* "(" space* exp space* ")" space*
op = "+" | "-" | "*" | "/"
numlit = digit+
digit = "0".."9"
space = " " | "\t"
Augh! All those “space*” occurrences make the description hard to read. But we’re using so, so let’s use the fact that if a rule name begins with a capital letter, it will be as if space* appears between all of the expressions on the right hand side. This gives us:
Exp = Exp op Exp
| numlit
| "-" Exp
| "(" Exp ")"
op = "+" | "-" | "*" | "/"
numlit = digit+
digit = "0".."9"
space = " " | "\t"
This simple but very powerful idea leads to some useful terminology: Lexical categories start with lowercase letters. Phrase categories start with capital letters. The lexical definitions show us how to combine characters into words and punctuation (called tokens), and the phrase definitions show us how to combine words and symbols into phrases (where the words and symbols can, if you wish, be surrounded by spacing).
But we still have problems. This grammar can parse the string 9-3*7 in two ways:
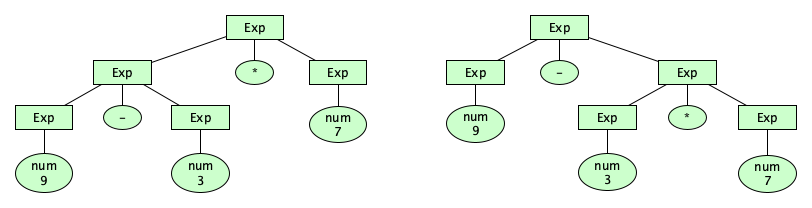
This means our syntax description is ambiguous. One way to get rid of the ambiguity is to add extra rules to build in an operator precedence:
Exp = Term (("+" | "-") Term)*
Term = Factor (("*" | "/") Factor)*
Factor = "-"? Primary
Primary = "(" Exp ")" | numlit
numlit = digit+
digit = "0".."9"
space = " " | "\t"
3*9-7.
This takes care of precedence concerns, but what if we wanted our grammar to specify associativity? We can do that too. Here is a way to make our binary operators left-associative:
Exp = Term | Exp ("+" | "-") Term
Term = Factor | Term ("*" | "/") Factor
Factor = Primary | "-" Primary
Primary = numlit | "(" Exp ")"
digit = "0".."9"
numlit = digit+
space = " " | "\t"
3-5-8-2*8-9-7-1 according to this grammar.
Abstract Syntax
We had to do a lot of specification work to define expressions as strings of characters. For example, we needed extra tokens (parentheses) and extra categories (Term, Factor, Primary) in order to capture precedence, and use other tricks to capture associativity. None of this crap matters if our languages were just trees! So let’s define function $\mathscr{A}$ to turn a phrase into an abstract syntax tree. We write trees in the form $\{A\;B\;C\;...\}$ where $A$ is the root and $B$, $C$, ... are the children.
$\mathscr{A}(E - T) = \{\mathsf{Minus}\;\mathscr{A}(E)\;\mathscr{A}(T)\}$
$\mathscr{A}(T * F) = \{\mathsf{Times}\;\mathscr{A}(T)\;\mathscr{A}(F)\}$
$\mathscr{A}(T\;/\;F) = \{\mathsf{Divide}\;\mathscr{A}(T)\;\mathscr{A}(F)\}$
$\mathscr{A}(-\;P) = \{\mathsf{Negate}\;\mathscr{A}(P)\}$
$\mathscr{A}(n) = \{\mathsf{Numlit}\;n\}$
$\mathscr{A}(\mathrm{(}\;E\;\mathrm{)}) = \mathscr{A}(E)$
Static Semantics
Think of how in a language like Java, an expression like x+5 looks beautifully well-formed and well-structured. But if $x$ hasn’t been declared, or has a type other than a number or string, the expression doesn’t mean anything. So while it is syntactically correct, it can be determined meaningless without ever running a program containing it.
Ael doesn’t have any semantic rules that can be checked statically. Perhaps we could imagine some.... If we had, say, limited all integer literals to 64 bits, we would probably put that requirement in the static semantics (even though in theory it is checkable in the syntax).
Dynamic Semantics
A dynamic semantics computes the meaning of an abstract syntax tree. In Ael, the meaning of expressions will be integer numeric values. Assuming the existence of a function $valueof$ for turning number tokens into numeric values, we’ll define function $\mathscr{E}$, mapping abstract syntax trees to value, as follows:
$\mathscr{E}\{\mathsf{Minus}\;e_1\;e_2\} = \mathscr{E}e_1 - \mathscr{E}e_2$
$\mathscr{E}\{\mathsf{Times}\;e_1\;e_2\} = \mathscr{E}e_1 \times \mathscr{E}e_2$
$\mathscr{E}\{\mathsf{Divide}\;e_1\;e_2\} = \mathscr{E}e_1 \div \mathscr{E}e_2$
$\mathscr{E}\{\mathsf{Negate}\;e\} = -\mathscr{E}e$
$\mathscr{E}\{\mathsf{Numlit}\;n\} = valueof(n)$
Applying the Specification
Let’s determine the meaning of this string:
-8 * (22- 7)
The character string is:
SPACE HYPHEN DIGIT EIGHT SPACE TAB ASTERISK SPACE LEFTPAREN DIGIT TWO DIGIT TWO HYPHEN SPACE SPACE DIGIT SEVEN RIGHTPAREN
Let’s apply the lexical rules to tokenize the string:
space
-
numlit(8)
space
space
*
space
(
numlit(22)
-
space
space
numlit(7)
)
The spaces will be skipped eventually, so we can just as well view the token stream like this:
-
numlit(8)
*
(
numlit(22)
-
numlit(7)
)
Parsing uncovers the derivation tree, also known as the concrete syntax tree:
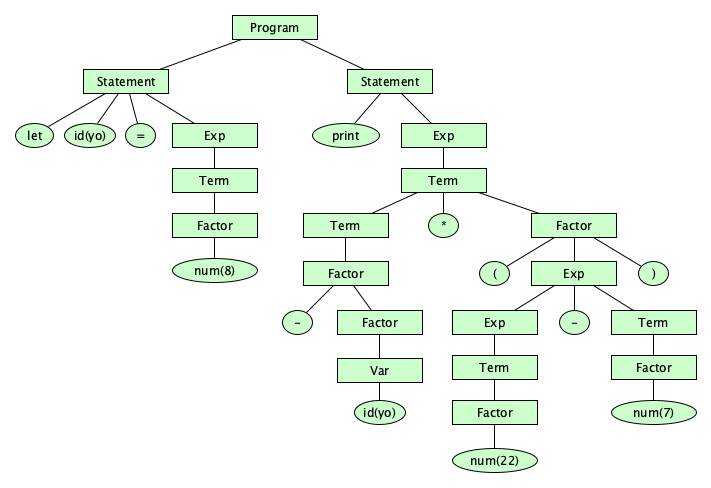
The static semantics is applied to the concrete syntax tree to produce the abstract syntax tree, namely: $$ \{ \mathsf{Times} \; \{ \mathsf{Negate} \; \{\mathsf{Numlit}\;8\} \} \{ \mathsf{Minus} \; \{\mathsf{Numlit}\;22\} \; \{\mathsf{Numlit}\;7\} \} \} $$
which might be a little easier to read like this: $$ \begin{array}{l} \{ \mathsf{Times} \\ \;\;\;\; \{ \mathsf{Negate} \; \{\mathsf{Numlit}\;8\} \} \\ \;\;\;\; \{ \mathsf{Minus} \; \{\mathsf{Numlit}\;22\} \; \{\mathsf{Numlit}\;7\} \} \} \end{array} $$
or even easier to read in tree form like this:
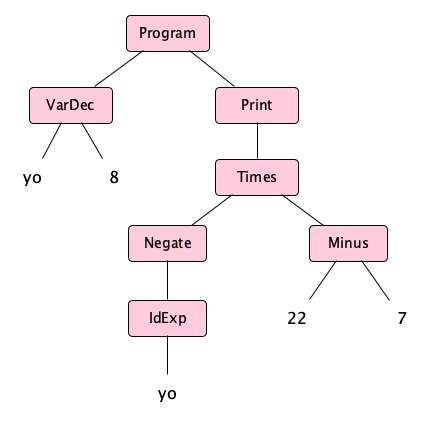
which, informally can be shortened to:
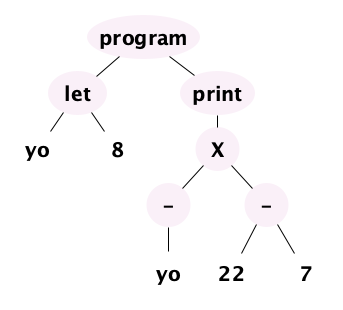
Notice how ASTs are way simpler than concrete trees. In fact in real compilers, unless the language is extraordinarily simple, you never see a concrete tree! Parsers generally go straight to the abstract syntax tree (though there are exceptions).
Finally, we apply the dynamic semantics to the AST to compute the meaning: \[ \begin{array}{l} \mathscr{E} \{\mathsf{Times}\;\{\mathsf{Negate}\;\{\mathsf{Numlit}\;8\}\}\{\mathsf{Minus}\;\{\mathsf{Numlit}\;22\}\;\{\mathsf{Numlit}\;7\}\}\} \\ \;\;\;\; = \mathscr{E} \{\mathsf{Negate}\;\{\mathsf{Numlit}\;8\}\} \times \mathscr{E}\{\mathsf{Minus}\;\{\mathsf{Numlit}\;22\}\;\{\mathsf{Numlit}\;7\}\}\} \\ \;\;\;\; = -\mathscr{E}\,\{\mathsf{Numlit}\;8\} \times (\mathscr{E}\{\mathsf{Numlit}\;22\} - \mathscr{E}\{\mathsf{Numlit}\;7\}) \\ \;\;\;\; = -8 \times (22-7) \\ \;\;\;\; = -8 \times 15 \\ \;\;\;\; = -120 \end{array} \]
98 * (247 - 6) / 3 / 100 - 701.
(* (- 8) (- 22 7)) is the actual way to write arithmetic expressions. Hint: several do exist. Why would anyone design a language this way?