Priority Queues

The Basics

A priority queue is a collection in which items can be added at any time, but the only item that can be removed is the one with the highest priority.

Operations

• add(x): add item x
• remove: remove the highest priority item
• peek: return the highest priority (without removing it)
• size: return the number of items in the priority queue
• isEmpty: return whether the priority queue has no items

Examples

• Patients in an emergency room
• Operating system scheduler
• Routing
• A* search
• Simulation
• Many more examples

Representations

Unsorted Array

• add is Θ(1) — just add the item at the end.
• peek is Θ(n) — must do linear scan to find.
• remove is Θ(n) — must find the element and compress the array.

Unsorted Linked List

• add is Θ(1) — just add the item at the end.
• peek is Θ(n) — must do linear scan to find.
• remove is Θ(n) — because the item must be found first.

Sorted Array

• add is Θ(n) — you can find where to insert in log time, but you have to make room in the array, which is linear.
• peek is Θ(1) — the value is at the end of the array.
• remove is Θ(1) — we can just whack the item off the end.

Sorted Linked List

• add is Θ(n) — you have to step through the chain to find the place to insert.
• peek is Θ(1) — the value is at the end of the array.
• remove is Θ(1) — we can just whack the item off the end.

Heap

• add is Θ(log n)
• peek is Θ(1)
• remove is Θ(log n)

What's a heap, anyway?

Heaps

A heap is a complete binary tree in which the value of a node is less than all the values in its subtrees. By convention, the smallest element is the one with the highest priority.

Peek

Therefore, the smallest element, the one with the highest priority, is always on top, so peek() is Θ(1).

Add

To insert, add the new item to the last slot in the array and sift it up.

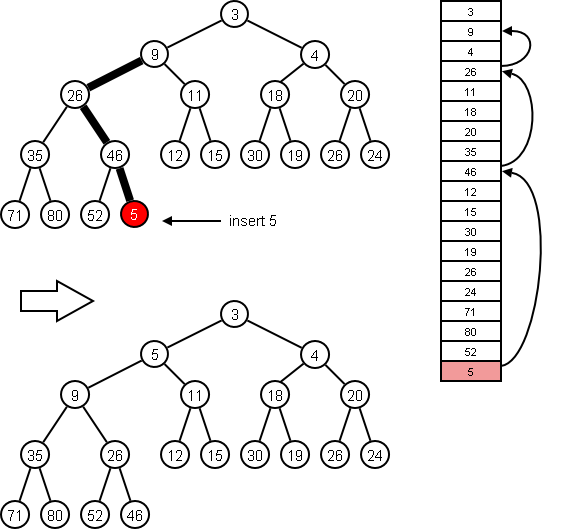
Since the tree is complete, it has minimum height, and the worst case number of moves up is logarithmic in the heap size. So cool.

Remove

To remove, return the value at the top, replace the top node with the value of the last slot, destroy the last slot, and sift down.

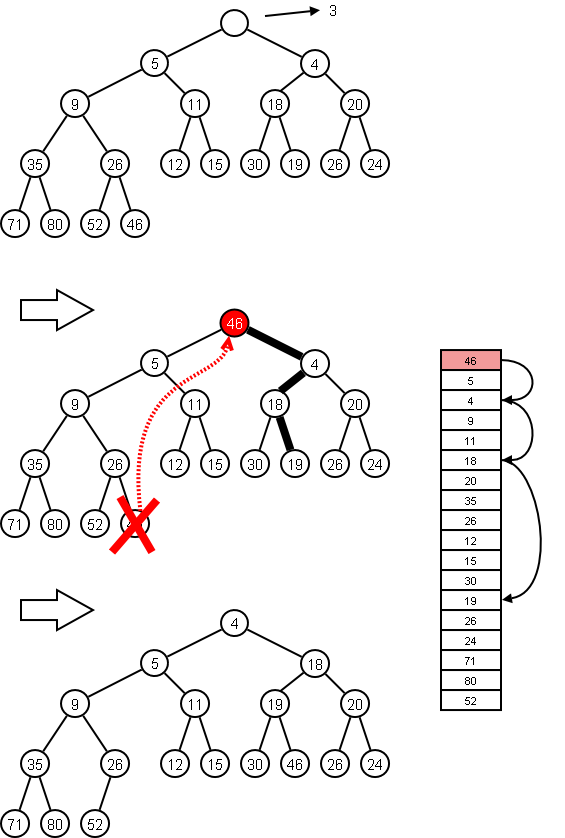
It should be pretty easy to prove that deletion is done in logarithmic time.

Heapify

A cool operation you'll sometimes see is called heapify — it turns a random array into a heap:

for (int i = a.length/2; i >= 0; i--) {
    siftdown(i);
}

More on Heaps

By the way...

• The heap described above is really a binary heap
• A binary heap is just a d-ary heap with d=2
• You might be interested in Fibonacci heaps, Pairing heaps, Skew heaps, Soft heaps, Binomial heaps, Leftist heaps, and Beaps.

Priority Queues in Java

There's already a PriorityQueue class in the Java Core API. It implements the Queue interface, and has the following characteristics:

• It is implemented with a heap
• It uses the element type's natural ordering or a comparator passed to the constructor
• The highest priority element is the smallest element
• add, offer, poll, and remove() run in Θ(log n) time
• peek, element, and size run in Θ(1) time
• The "convenience methods" remove(Object) and contains(Object) run in Θ(n) time
• It is not thread-safe

There's also the PriorityBlockingQueue class.

Implementation From Scratch

However we're going to write a PriorityQueue class from scratch because:

• This is the only way for you to really learn how priority queues work.
• You need coding practice.
• You need to know how to code things up when you find yourself in a very restrictive environment that doesn't have a collections library.

We'll develop this during class

Unit Testing

Here are some of the things we need to test:

• A queue is empty on construction
• A queue has size 0 on construction
• After n enqueues to an empty queue, n > 0, the queue is not empty and its size is n
• If the size is n, then after n dequeues, the stack is empty and has a size 0
• If one enqueues the values 1 through 50, in some random order, into an empty queue, then if 50 dequeues are done the values dequeued are 1 through 50, respectively
• Dequeueing from an empty queue does throw a NoSuchElementException
• Peeking into an empty queue does throw a NoSuchElementException

Here is a rough unit test:

We'll develop this during class

Priority Queues in Ruby

Here's a binary heap-based, non-thread-safe, non-blocking, implementation in Ruby:

# A priority queue class

class PriorityQueue
  def initialize
    @heap = []
  end

  # Add an element to the queue
  def add!(x)
    @heap << x
    sift_up(@heap.length - 1)
    self
  end

  # Return the smallest element in the queue
  def peek
    @heap[0]
  end

  # Remove the smallest element from the queue
  def remove!()
    raise RuntimeError, "Empty Queue" if @heap.length == 0
    if @heap.length == 1
      @heap = []
    else
      @heap[0] = @heap.pop
      sift_down(0)
    end
    self
  end

  private

  # Sift up the element at index i
  def sift_up(i)
    parent = (i - 1) / 2
    if parent >= 0 and @heap[parent] > @heap[i]
      @heap[parent], @heap[i] = @heap[i], @heap[parent]
      sift_up(parent)
    end
  end

  # Sift down the element at index i
  def sift_down(i)
    child = (i * 2) + 1
    return if child >= @heap.length
    child += 1 if child + 1 < @heap.length and @heap[child] > @heap[child+1]
    if @heap[i] > @heap[child]
      @heap[child], @heap[i] = @heap[i], @heap[child]
      sift_down(child)
    end
  end
end

And here's a unit test

require 'test/unit'
require 'priorityqueue'

class PriorityQueueTest < Test::Unit::TestCase

  def test_new
    q = PriorityQueue.new
    assert_equal(q.peek, nil)
    assert_raise(RuntimeError) {q.remove!}
  end

  # Add 1..100 in at random, they should come out in order
  def test_adds_and_removes
    q = PriorityQueue.new
    (1..100).to_a.sort_by {rand}.each {|x| q.add!(x)}
    1.upto(100) do |i|
      assert_equal(q.peek, i)
      q.remove!
    end
  end
end