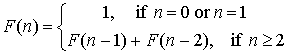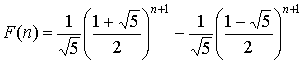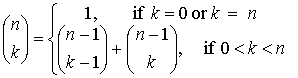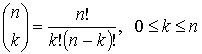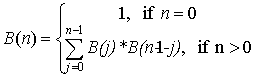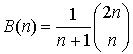Recursion

Recursive Definitions

Finite sets can be defined by enumerating their elements, but infinite sets cannot. Some infinite sets are "built up" by rules. These rules constitute a recursive, or inductive definition of the set. Examples:

Note the importance of the "nothing else" clauses; without them your definitions are not unique.

Be careful with these definitions! Self reference can get you into trouble.

x =_def cos(x)

You got lucky here; this uniquely defines x

x =_def x

ERROR: This is a circular definition, and therefore does not define anything!

x =_def x + 1

ERROR: There's no such x, assuming we're taking about finite numbers here

x =_def 6 - x²

DUBIOUS: x could be 2 or -3

Recursive Functions

Writing functions recursively usually results in smaller, more concise, more elegant and easier-to-understand code. It might be less efficient, though.

You MUST:

1. have a base case
2. ensure that each recursive call makes progress toward the base case.

Examples:

import java.math.BigInteger;

/**
 * A utility class with several examples of recursion. The example methods were
 * chosen because they are short and concise examples, not because they are good
 * code. In fact, nearly every method shown here is inferior to its iterative
 * counterpart.
 */
public class RecursionExamples {

    /**
     * Returns whether or not s is the same forwards and backwards. Directly
     * implements the inductive definition. INEFFICIENT: DO NOT USE IN PRACTICE.
     */
    public static boolean isPalindrome(String s) {
        return (s.length() <= 1)
                || (s.charAt(0) == s.charAt(s.length() - 1)
                        && isPalindrome(s.substring(1, s.length() - 1)));
    }

    /**
     * Returns the factorial of its argument INEFFICIENT: DO NOT USE IN PRACTICE.
     */
    public static long factorial(int n) {
        return (n <= 0) ? 1 : n * factorial(n - 1);
    }

    /**
     * Returns the log-base-2 of it argument. INEFFICIENT: DO NOT USE IN PRACTICE.
     */
    public static int log(int n) {
        if (n <= 0) {
            throw new IllegalArgumentException();
        } else if (n == 1) {
            return 0;
        } else {
            return 1 + log(n / 2);
        }
    }

    /**
     * Returns the sum of the digits of a given integer, e.g., sumOfDigits(538) = 5
     * + 3 + 8 = 16. INEFFICIENT: DO NOT USE IN PRACTICE.
     */
    public static int sumOfDigits(int n) {
        if (n < 0) {
            return sumOfDigits(-n);
        } else if (n < 10) {
            return n;
        } else {
            return sumOfDigits(n / 10) + (n % 10);
        }
    }

    /**
     * Returns the nth Fibonacci number. These numbers are the sequence f(0)=0,
     * f(1)=1, f(2)=1, f(3)=2, f(4)=3, f(5)=5, f(6)=8, f(7)=13, etc. Note that for
     * n>1, f(n)=f(n-1)+f(n-2). HORRIFICALLY INEFFICIENT: DO NOT USE IN PRACTICE.
     */
    public static BigInteger fibonacci(int n) {
        if (n < 0) {
            throw new IllegalArgumentException();
        }
        return n <= 1 ? BigInteger.valueOf(n) : fibonacci(n - 1).add(fibonacci(n - 2));
    }

    /**
     * Returns the greatest common divisor of a and b. This is tail recursive, so a
     * good compiler will generate code to make it run as fast as its iterative
     * cousin (except that the negative check will occur every time through the loop
     * unless the compiler is really, really smart.)
     */
    public static int gcd(int a, int b) {
        if (a < 0 || b < 0) {
            throw new IllegalArgumentException("No GCD of negative integers");
        }
        return b == 0 ? a : gcd(b, a % b);
    }
}

Understanding Recursive Functions

It is strongly suggested that you evaulate recursive functions by hand to get comfortable with them. Here are examples.

isPalindrome("racecar")
  = ('r' == 'r') && isPalindrome("aceca")
  = true && isPalindrome("aceca")
  = ('a' == 'a') && isPalindrome("cec")
  = true && isPalindrome("cec")
  = ('c' == 'c') && isPalindrome("a")
  = true && isPalindrome("a")
  = true

factorial(4)
  = 4 * factorial(3)
  = 4 * (3 * factorial(2))
  = 4 * (3 * (2 * factorial(1)))
  = 4 * (3 * (2 * (1 * factorial(0))))
  = 4 * (3 * (2 * (1 * 1)))
  = 4 * (3 * (2 * 1))
  = 4 * (3 * 2)
  = 4 * 6
  = 24

log(100)
  = 1 + log(50)
  = 1 + 1 + log(25)
  = 1 + 1 + 1 + log(12)
  = 1 + 1 + 1 + 1 + log(6)
  = 1 + 1 + 1 + 1 + 1 + log(3)
  = 1 + 1 + 1 + 1 + 1 + 1 + log(1)
  = 1 + 1 + 1 + 1 + 1 + 1 + 0
  = 6

sumOfDigits(-48729)
  = sumOfDigits(48279)
  = sumOfDigits(4827) + 9
  = (sumOfDigits(482) + 7) + 9
  = ((sumOfDigits(48) + 2) + 7) + 9
  = (((sumOfDigits(4) + 8) + 2) + 7) + 9
  = (((4 + 8) + 2) + 7) + 9
  = ((12 + 2) + 7) + 9
  = (14 + 7) + 9
  = 21 + 9
  = 30

fib(4)
  = fib(3) + fib(2)
  = (fib(2) + fib(1)) + fib(2)
  = ((fib(1) + fib(0)) + fib(1)) + fib(2)
  = ((1 + fib(0)) + fib(1)) + fib(2)
  = ((1 + 0) + fib(1)) + fib(2)
  = (1 + fib(1)) + fib(2)
  = (1 + 1) + fib(2)
  = 2 + fib(2)
  = 2 + (fib(1) + fib(0))
  = 2 + (1 + fib(0))
  = 2 + (1 + 0)
  = 2 + 1
  = 3

gcd 444 93
  = gcd 93 72
  = gcd 72 21
  = gcd 21 9
  = gcd 9 3
  = gcd 3 0
  = 3

When not to use Recursion

Don't recurse when a simple loop will do

Factorial should be written like this:

public static int factorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; i++) {
        result *= i;
    }
    return result;
}

Don't recurse when it causes duplication of work

Often needless recursion turns linear into EXPONENTIAL complexity!

// HORRIFIC CODE for computing the nth Fibonacci Number
static int fib(int n) {
    return n <= 1 ? 1 : fib(n-2) + fib(n-1);
}

The function above makes 25 calls to fib just to determine that the value of fib(6) is 13.

    fib(6)
        calls fib(5)
            which calls fib(4)
                which calls fib(3)
                    which calls fib(2)
                        which calls fib(1)
                        and fib(0)
                    and fib(1)
                and fib(2)
                    which calls fib(1)
                    and fib(0)
            and fib(3)
                which calls fib(2)
                    which calls fib(1)
                    and fib(0)
                and fib(1)
        and fib(4)
            which calls fib(3)
                which calls fib(2)
                    which calls fib(1)
                    and fib(0)
                and fib(1)
            and fib(2)
                which calls fib(1)
                and fib(0)

Here is another disastrous example:

/**
 * Horrific Code for determining the minimum number of coins
 * needed to make n cents where the coin values are stored in the
 * array denominations.  The denominations array must contain
 * a 1 in it, or the result of this method is undefined.
 */
static int minimumNumberOfCoins(int n, int[] denominations) {
    int minimumSoFar = n; // the most you could need is n
    for (int d : denominations)
        if (d == n) {
            return 1;
        } else if (d < n) {
            minimumSoFar = Math.min(minimumSoFar,
                minimumNumberOfCoins(n-d, denominations));
        }
    return minimumSoFar;
}

Memoization

One way to avoid duplicating work is simply to cache the partial results as you see them. Here is an example application that compares recursive and non-recursive ways of generating binomial coefficients

/**
 * An application that analyzes two algorithms for computing Binomial
 * Coefficients and displays a report to standard output. The first one is a
 * "fast" one which essentially fills out Pascal's triangle; the second
 * moronically applies the well-known recurrence relation. Each analysis
 * displays a table where each row is the value of n in a call of C(n,n/2)
 * followed by the result of C(n,n/2) followed by the ratio of the actual
 * running time to two candidate time complexity functions. (This is a standard
 * way to empirically determine a complexity class - just see if a column
 * remains pretty much constant.)
 */
public class BinomialCoefficientGenerator {

    private static class Slow {

        /**
         * Computes Choose(n,k) the slow way by directly implementing the recurrence
         * relation.
         */
        public static int C(int n, int k) {
            if (k < 0 || k > n) {
                throw new IllegalArgumentException("Can't do C(" + n + "," + k + ")");
            } else if (k == 0 || n == k) {
                return 1;
            } else {
                return C(n - 1, k) + C(n - 1, k - 1);
            }
        }

        /**
         * Times various runs of C(n,k) looking for whether n^2 or 2^n is the best
         * empirical estimate of the complexity.
         */
        public static void analyze() {
            System.out.println("\nAnalyzing Horrible Recursive Solution");
            System.out.println("Testing ratios for n^2 and 2^n");
            for (int n = 20; n < 30; n += 1) {
                long start = System.currentTimeMillis();
                int result = C(n, n / 2);
                long stop = System.currentTimeMillis();
                double duration = stop - start;
                System.out.printf("%5d%20d%20.14f%20.14f\n", n, result, duration / (n * n),
                        duration / Math.pow(2.0, n));
            }
        }
    }

    private static class Fast {

        /**
         * Computes Choose(n,k) by filling out Pascal's triangle.
         */
        public static int C(int n, int k) {
            if (k < 0 || k > n) {
                throw new IllegalArgumentException("Can't do C(" + n + "," + k + ")");
            }
            int[][] cache = new int[n + 1][n + 1];
            for (int i = 0; i <= n; i++) {
                cache[i][0] = cache[i][i] = 1;
                for (int j = 1; j <= i - 1; j++) {
                    cache[i][j] = cache[i - 1][j] + cache[i - 1][j - 1];
                }
            }
            return cache[n][k];
        }

        /**
         * Times various runs of C(n,k) looking for whether nlogn or n^2 is the best
         * empirical estimate of the complexity.
         */
        public static void analyze() {
            System.out.println("\nAnalyzing Dynamic Programming Solution");
            System.out.println("Testing ratios for n*log(n) and n^2");
            System.out.println("Note that overflow is ignored");
            for (int n = 500; n < 1500; n += 100) {
                long start = System.currentTimeMillis();
                int result = C(n, n / 2);
                long stop = System.currentTimeMillis();
                double duration = stop - start;
                System.out.printf("%5d%20d%20.14f%20.14f\n", n, result, duration / (n * Math.log(n)),
                        duration / (n * n));
            }
        }
    }

    /**
     * Runs each version.
     */
    public static void main(String[] args) {
        Fast.analyze();
        Slow.analyze();
    }
}

Useful Examples of Recursion

Recursion is most useful when

• You can't easily replace it with a simple loop because the structure is being processed "backwards"
• You need to do a multiway recursion but you are careful to avoid duplicating work
• You are implementing and algorithm using a known paradigm like backtracking or dynamic programming
• The recursion is a tail recursion which you know your compiler will optimize away

Here's an example of multi-way recursion without duplication:

import java.util.function.Consumer;

/**
 * Utility class containing a permutation generation method.
 */
public class Permuter {

    /**
     * Writes all permutations of the characters in s to standard output, separated
     * by newlines.
     */
    public static void permute(String string, Consumer<String> consumer) {
        permute("", string, consumer);
    }

    /**
     * Helper method: attaches all permutations of leftOver onto prefix and prints
     * them all.
     */
    private static void permute(String prefix, String leftOver,
            Consumer<String> consumer) {
        if (leftOver.isEmpty()) {
            consumer.accept(prefix);
        } else {
            for (var i = 0; i < leftOver.length(); i++) {
                permute(prefix + leftOver.charAt(i),
                        leftOver.substring(0, i) + leftOver.substring(i + 1), consumer);
            }
        }
    }

    /**
     * Invokes permute on the command line argument.
     */
    public static void main(String[] args) {
        if (args.length == 0) {
            System.out.println("Needs an argument string to permute");
        } else {
            permute(args[0], System.out::println);
        }
    }
}

Closed Forms

Some recursive functions have closed forms, though there is no guarantee computing the closed form will be any more efficient.

Inductive Proofs

Suppose you wanted to prove that every element in a recursively defined set had some property. You can't prove the property for each element because there are an infinite number of elements. But you can prove the property for the basis elements and then show that elements generated by the recursive rules maintain the property whenever the elements from which they were generated have the property. Example:

Prove: The successor of every odd number is divisible by 2.
Proof: Basis: The successor of 1 is 2 and 2 is divisible by 2. Step: Assume k is odd and k+1 is divisible by 2. We have to show under these assumptions that (1) the successor of k-2 is divisible by 2 and (2) the successor of k+2 is divisible by 2. To prove (1) we note that the successor of k-2 is k-1 which is divisible by 2 because k-1 = k+1-2. To prove (2) note that the successor of k+2 is k+3 which is divisible by 2 because k+3 = k+1+2. This completes the proof.

Recursive Datatypes

Often you'll have a datatype whose components are (references to) objects of the datatype itself. For example

which would look something like

class Person {
    String name;
    Date birthday;
    double height;
    Person mother;
    Person father;
    ...
}

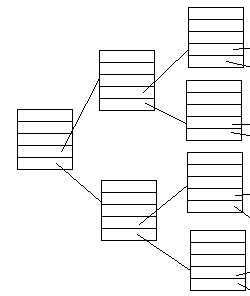
Most of the methods operating on such a class would naturally be recursive:

public int lengthOfKnownMaternalLine() {
    if (mother == null) {
        return 0;
    } else {
        return 1 + mother.lengthOfKnownMaternalLine();
    }
}