Trees

Motivation

Humans deal with complexity in several ways, most notably via abstraction (suppression of details), classification (grouping, naming, tagging), and hierarchy. Here are examples of hierarchical arrangements of objects, starting with an example from geography:

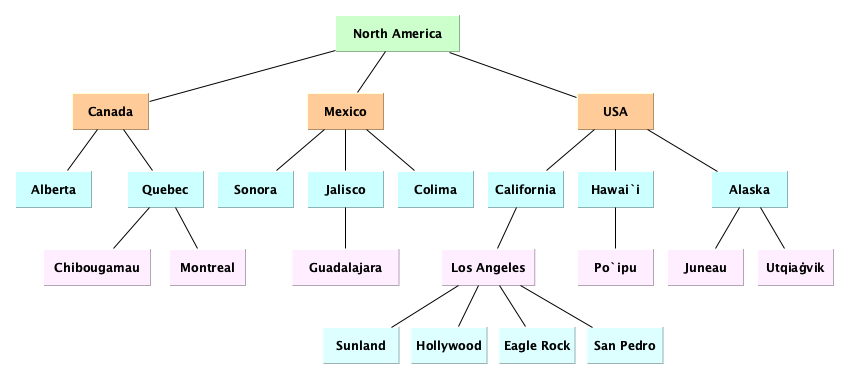
Here is an example showing that a book has a hierarchical structure:

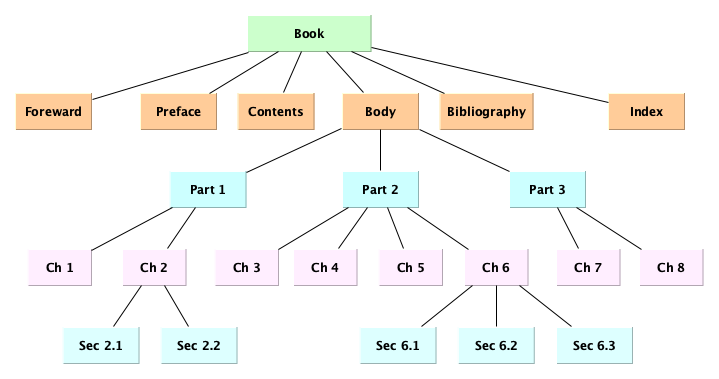
The structure of a computer program is often tree-shaped, for example:

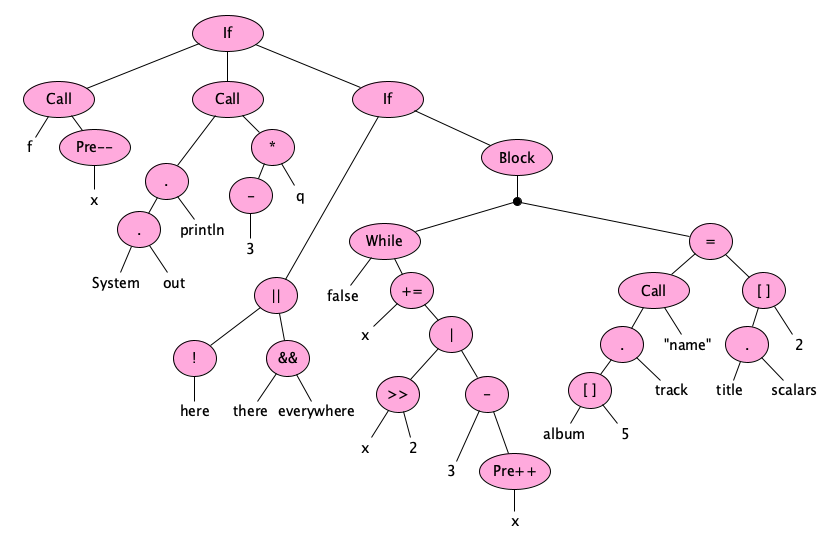
File systems are a classic example of hierarchy:

  /
  ├── Library
  │   ├── Fonts
  │   │   ├── Farisi.ttf
  │   │   ├── GillSans.ttf
  │   │   └── Sana.ttc
  │   └── Keychains
  │       └── System.keychain
  ├── Users
  │   ├── jessica
  │   │   ├── homework
  │   │   │   ├── hw1.py
  │   │   │   └── hw2.txt
  │   │   └── resume.pdf
  │   └── kimiko
  │       ├── IMG0001.jpg
  │       └── IMG0002.jpg
  └── bin
      ├── date
      ├── hostname
      ├── kill
      └── sleep

And if you’ve done any web development, you’ve worked with a DOM tree:

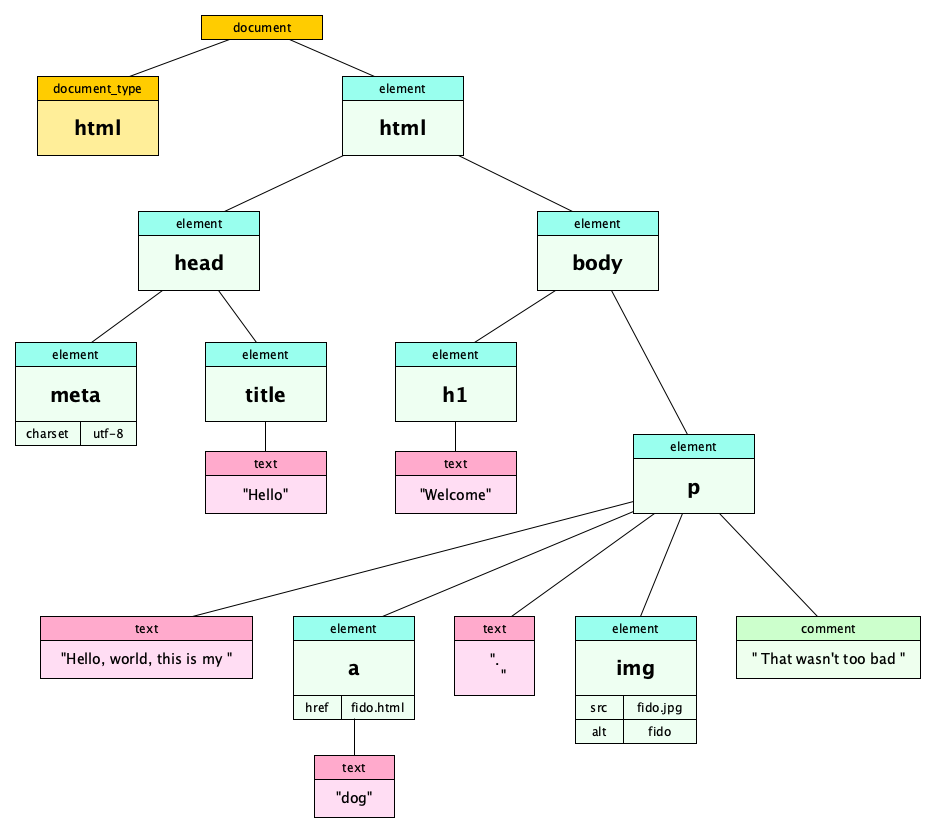
It’s important to know that this tree, known as the DOM, or Document Object Model is exactly the data structure used in web browsers. Knowledge of this tree is absolutely essential for web programmers as front-end web development involves the styling and manipulation of the DOM. The operations to manipulate the DOM all use the language of trees.

Spend some time making observations about these data arrangements. Here are a few to get you started: (1) There are no “cycles” among the nodes in a tree. (2) They are usually drawn upside down with the “root” at the top. (3) For some trees, the order of the “children” of a node seem significant (like in the book, expression, and HTML examples), but in other cases it does not (like in the geography and file system examples). What other observations can you make?

More Motivation

These hierarchies have an interesting “look” to them: the various objects are arranged with connectors between them in such a way that there are no cycles. This idea shows up in other places! When finding minimal connectivity in networks, we get this kind of structure:

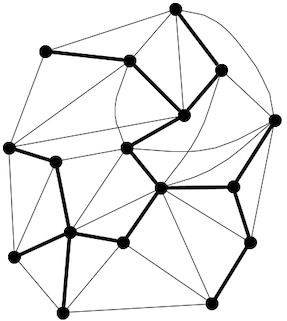
We can also arrange items this way to make it possible to do extremely efficient search, spell checking and autocomplete.

Looks like we are on to something here. The science in computer science gets us wondering if there is anything deeper here to study. These connected, cycle-free arrangements, remind us of trees, so that’s what we will call them. Now let’s build up a theory to get us primed to do great things.

Talking About Trees

It is good to have a vocabulary surrounding trees so we can talk about them precisely and start using them in computer programming. Let’s start with the basics.

Nodes and Edges

Here’s a tree:

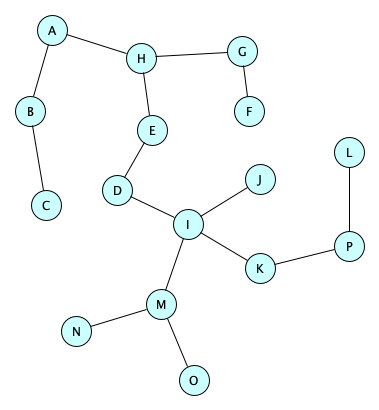
And here is some vocabulary:

Node

(a.k.a. vertex) A data element in the tree

Edge

(a.k.a. branch, or link) A connection between two distinct nodes

Tree

A collection of nodes and edges such that (1) there are no cycles, and (2) every node is reachable from every other node

Empty Tree

A tree with zero nodes

Singleton Tree

A tree with only one node

Size

The number of nodes in the tree

Paths

We are going to store data in trees, and so trees are a kind of data structure. And what do we do with data structures? We navigate through them. For trees, the way we navigate is through paths.

Path

A sequence $\langle n_0\,n_1\,n_2\,\ldots\,n_k\rangle$ where $k \geq 0$ and there exists an edge connecting $n_{i-1}$ and $n_i$

Start(p)

The first node in the path, $n_0$

End(p)

The last node in the path, $n_k$

Length(p)

The number of edge occurrences, $k$

Simple Path

A path in which all nodes are distinct

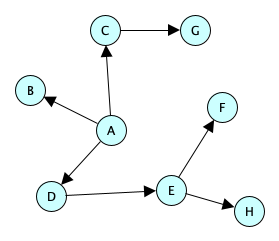
Oriented Trees

The tree above did not look like the pictures of hierarchies that came before. All of the hierarchies had a special node at the top and all the edges seemed to grow outward from it. Ah, so there are at least two different kinds of trees:

Free Tree

A tree with no distinguished nodes and no directions on the edges

Oriented Tree

A tree with a distinguished node, called the root, and with every edge directed away from the root.

Here is an oriented tree:

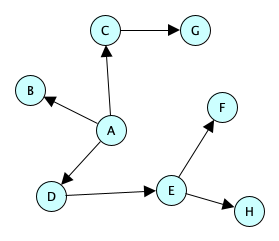
If drawn with the root at the top and all edges pointing downward (as is conventional) then the arrows are redundant and often omitted. Like so:

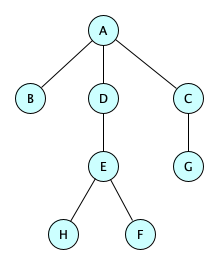
So yeah, sometimes the only way to tell if a particular picture of a tree is representing a free or an oriented tree is by context.

Oriented trees introduce a lot more vocabulary. Here are many of the important terms.

Rather than explicit definitions, we’re going to explain the terms relative to the example oriented tree we just saw.

Parent

$A$ is the parent of $B$ and $C$ and $D$

Children

The children of $A$ are $B$ and $C$ and $D$

Siblings

$B$ and $C$ are siblings

Root node

The only node without a parent

Leaf node

A node without children

Degree(n)

The number of children of $n$

Degree(t)

The greatest degree of the nodes in $t$

Level(n)

Level(n) = if $n$ is the root then 0 else 1 + Level(Parent($n$))

Depth(n)

Same as Level($n$)

Height(n)

Maximum length over all paths from $n$ to a leaf

Height(t)

The height of $t$’s root node

Width(t)

The size of its largest level of $t$

Ancestors(n)

Ancestors(n) = if $n$ is the root then $\varnothing$ else {Parent($n$)} $\cup$ Ancestors(Parent($n$))

Descendants(n)

The set of all nodes reachable from $n$ following the edges leaving it in the direction of the arrows

PathLength(t)

The sum of all the depths of all the nodes in $t$

Subtree(n)

The subtree rooted at $n$

$k$-node

A node with $k$ children. A 0-node is a leaf. A 1-node has exactly one child. A 2-node has exactly two children. And so on.

Ordered Trees

Remember in the examples above that int the book and HTML trees, the order mattered, but that in the geography and file system examples, it did not? We actually have a special word for the former, and some variations of interest.

Ordered Tree

An oriented tree in which the ordering of the children matters (strictly speaking, the children form a list, rather than a set)

$k$-ary Tree

An ordered tree in the children of each node have a unique index position $\in 0 \ldots k-1$ for some integer $k \geq 0$

Binary Tree

A 2-ary Tree

Trinary (a.k.a. Ternary) Tree

A 3-ary Tree

Fibonacci Tree

A tree from the set of trees defined inductively as: (1) $F_0$ is the empty tree, (2) $F_1$ is a tree with only one node, and (3) $F_{k+2}$ is a node whose left subtree is a $F_{k+1}$ tree and whose right subtree is a $F_k$ tree.

Binomial Trees

$B_k$ consists of a node with $k$ children: the first of which is the root of a $B_{k-1}$ tree, the second is the root of a $B_{k-2}$ tree, etc.

Uses of Trees

Earlier we mentioned three places where trees tended to show up. Let’s review them here and connect them to the kinds of trees we just defined:

Representations

Circles and lines are commonly used to show trees, but there are other ways. Here are a few notations people have used in the past for oriented trees. Maybe you can think up sone on your own, too.

Outline

This notation for oriented trees is hopefully self-explanatory:

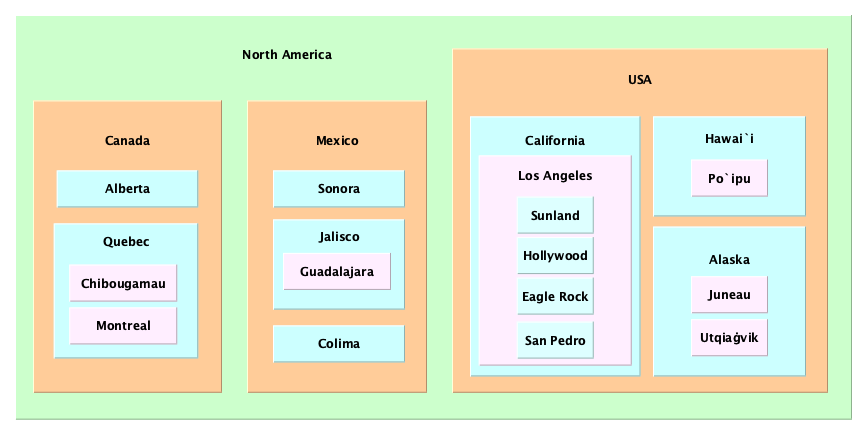
North America
    Canada
        Alberta
        Quebec
            Chibougamau
            Montreal
    Mexico
        Sonora
        Jalisco
            Guadalajara
        Colima
    USA
        California
          Los Angeles
              Sunland
              Hollywood
              Eagle Rock
              San Pedro
        Hawai`i
            Po`ipu
        Alaska
            Juneau
            Utqiaġvik

Table (Array)

Since every node in an oriented tree has zero or one parent, we can store a tree very compactly by keeping only the index of the parent together with the data in the node, for example:

    ┌───────────────┬────┐
  0 │               │    │
    ├───────────────┼────┤
  1 │ Mexico        │  5 │
    ├───────────────┼────┤
  2 │ Los Angeles   │ 17 │
    ├───────────────┼────┤
  3 │ Po`ipu        │ 15 │
    ├───────────────┼────┤
  4 │ Hollywood     │  2 │
    ├───────────────┼────┤
  5 │ North America │  0 │
    ├───────────────┼────┤
  6 │ Montreal      │  8 │
    ├───────────────┼────┤
  7 │ San Pedro     │  2 │
    ├───────────────┼────┤
  8 │ Quebec        │ 11 │
    ├───────────────┼────┤
  9 │ Alberta       │ 11 │
    ├───────────────┼────┤
 10 │ Chibougamau   │  8 │
    ├───────────────┼────┤
 11 │ Canada        │  5 │
    ├───────────────┼────┤
 12 │ Eagle Rock    │  2 │
    ├───────────────┼────┤
 13 │ Colima        │  1 │
    ├───────────────┼────┤
 14 │ Sonora        │  1 │
    ├───────────────┼────┤
 15 │ Hawai`i       │ 19 │
    ├───────────────┼────┤
 16 │ Guadalajara   │ 20 │
    ├───────────────┼────┤
 17 │ California    │ 19 │
    ├───────────────┼────┤
 18 │ Alaska        │ 19 │
    ├───────────────┼────┤
 19 │ USA           │  5 │
    ├───────────────┼────┤
 20 │ Jalisco       │  1 │
    ├───────────────┼────┤
 21 │ Juneau        │ 19 │
    ├───────────────┼────┤
 22 │ Utqiaġvik     │ 19 │
    ├───────────────┼────┤
 23 │ Sunland       │  2 │
    └───────────────┴────┘

Venn Diagram

Interestingly, nested structures exhibit a natural hierarchy, making it suitable for oriented trees:

String

The outline representation we saw earlier forces us to put each item on its own line. We can use parentheses to give us much more flexibility. Each node has the form (root subtree subtree ...)

(North America
    (Canada Alberta (Quebec Chibougamau Montreal))
    (Mexico
        Sonora
        (Jalisco Guadalajara)
        Colima)
    (USA
        (California
          (Los Angeles
              Sunland
              Hollywood
              Eagle Rock
              San Pedro))
        (Hawai`i Po`ipu)
        (Alaska Juneau Utqiaġvik)))

There are several variations on string representations. By way of example, the representation of the DOM tree we saw earlier can be expressed as a string in the Hypertext Markup Language, HTML, as follows:

<!doctype html>
<html>
  <head>
    <meta charset="utf-8">
    <title>Hello</title>
  </head>
  <body>
    <h1>Welcome</h1>
    <p>Hello, world, this is my <a href="fido.html">dog</a>.
      <img src="fido.jpg" alt="fido">
      <!-- That wasn't too bad -->
    </p>
  </body>
</html>

Representations of Free Trees

Free trees don’t have a root, so we pretty much treat them as graphs, and can use any one of the many known graph representations (adjacency list, adjacency matrix, incidence list), which we will study later when looking at graphs. For now, we’ll be focusing exclusively on oriented trees.

Operations on Oriented Trees

How many operations can we think of? Let’s see. For a tree $t$ and a node $n$, we can imagine:

• $t$.size $\longrightarrow$ an integer
• $t$.root $\longrightarrow$ an optional node
• $t$.height $\longrightarrow$ an integer
• $t$.width $\longrightarrow$ an integer
• $n$.parent $\longrightarrow$ an optional node
• $n$.children $\longrightarrow$ a set of nodes List if tree is ordered
• $n$.previousSibling $\longrightarrow$ an optional node Ordered Trees Only
• $n$.nextSibling $\longrightarrow$ an optional node Ordered Trees Only
• $n$.isRoot $\longrightarrow$ boolean
• $n$.isLeaf $\longrightarrow$ boolean
• $n$.height $\longrightarrow$ an integer
• $n$.depth $\longrightarrow$ an integer
• $n$.degree $\longrightarrow$ an integer
• $t$.frontier $\longrightarrow$ a set of nodes List if tree is ordered
• $n$.pathFromRoot $\longrightarrow$ a list of nodes
• $n$.ancestors $\longrightarrow$ a list of nodes
• $n$.isAncestorOf($n'$) $\longrightarrow$ a boolean
• $n$.isDescendantOf($n'$) $\longrightarrow$ a boolean
• $n$.pathTo($n'$) $\longrightarrow$ an optional list of nodes

Sometimes we will be traversing trees, performing operations on each node as we go. Two popular approaches to traversal are:

So we can add the operations:

• $t$.breadthFirst($consumer$) $\longrightarrow$ void
• $t$.depthFirst($consumer$) $\longrightarrow$ void

When traversing, it is assumed you always process the children in the proper order in ordered trees.

Implementations

Implementing trees is such a big topic, because there are so many kinds of trees. Let’s get a big picture before diving into programming.

• Free trees are really only used in graph applications, so we’ll wait until we study graphs to deal with these. In fact, free trees really are just a kind of graph, so there really aren’t any special representations of them apart from the usual graph implementations.
• The nodes of k-ary trees have a fixed-size array for their children, indexed from 0 through $k-1$. Generally we will have both an empty tree class and a tree node class, though sometimes you will see representations using nulls.
• General Oriented and Ordered trees (which are not $k$-ary) are generally identified with (or conflated with) their root nodes, or the designated root is simply held somewhere “outside” the tree. Each node holds some data and has a set, or list, of children. We rarely, if ever, care about empty trees, except in specialized cases.

In practice, $k$-ary trees are so prevalent, with so many applications and so many variations, that we have a whole separate page of notes on them.

For now, though, let’s take a quick peek at how a plain-old ordered tree (with no bounds on the number of children) would be represented in Java. Note that there’s no real distinction between the tree and its root: we just deal with nodes and just straight up treat a node as the root of “its” tree. We are only going to write a small number of methods; you can write the rest:

import java.util.List;
import java.util.Queue;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.function.Consumer;

public class TreeNode<T> {

    private T data;
    private List<TreeNode<T>> children = new ArrayList<>();

    public TreeNode(T data) {
        this.data = data;
    }

    public TreeNode<T> appendChild(T item) {
        var newNode = new TreeNode<>(item);
        children.add(newNode);
        return newNode;
    }

    public int size() {
        return 1 + children.stream().mapToInt(TreeNode::size).sum();
    }

    public boolean isLeaf() {
        return children.isEmpty();
    }

    public int height() {
        return isLeaf() ? 0
                : 1 + children.stream().mapToInt(TreeNode::height).max().orElse(0);
    }

    public void depthFirst(Consumer<T> consumer) {
        consumer.accept(data);
        children.forEach(node -> node.depthFirst(consumer));
    }

    public void breadthFirst(Consumer<T> consumer) {
        Queue<TreeNode<T>> queue = new LinkedList<>();
        queue.offer(this);
        while (!queue.isEmpty()) {
            var node = queue.remove();
            consumer.accept(node.data);
            for (var child : node.children) {
                queue.offer(child);
            }
        }
    }

    @Override
    public String toString() {
        var builder = new StringBuilder("(");
        builder.append(data);
        for (var child : children) {
            builder.append(child.toString());
        }
        builder.append(")");
        return builder.toString();
    }
}

How is the tree used? This gives you an idea:

public class TreeNodeExample {
    public static void main(String[] args) {
        var nodeA = new TreeNode<String>("A");
        var nodeB = nodeA.appendChild("B");
        var nodeC = nodeA.appendChild("C");
        nodeB.appendChild("D");
        nodeB.appendChild("E");
        nodeB.appendChild("F");
        var nodeG = nodeC.appendChild("G");
        nodeC.appendChild("H");

        System.out.printf("Here is a tree: %s%n", nodeA);
        System.out.printf("It has size %d%n", nodeA.size());
        System.out.printf("It has height %d%n", nodeA.height());
        System.out.printf("Is B a leaf? %b%n", nodeB.isLeaf());
        System.out.printf("Is G a leaf? %b%n", nodeG.isLeaf());
        System.out.println("Here are the nodes in depth first order:");
        nodeA.depthFirst(System.out::println);
        System.out.println("Here are the nodes in breadth first order:");
        nodeA.breadthFirst(System.out::println);
    }
}

$ javac TreeNodeExample.java && java TreeNodeExample
Here is a tree: (A(B(D)(E)(F))(C(G)(H)))
It has size 8
It has height 2
Is B a leaf? false
Is G a leaf? true
Here are the nodes in depth first order:
A
B
D
E
F
C
G
H
Here are the nodes in breadth first order:
A
B
C
D
E
F
G
H
[/Users/ray/git-repos/personal-site/code/java/collections] 

Summary