Uninformed Search

Just do it.

Overview

An uninformed (a.k.a. blind, brute-force) search algorithm generates the search tree without using any domain specific knowledge.

The two basic approaches differ as to whether you check for a goal when a node is generated or when it is expanded.

Checking at generation time:

if start_state is a goal state return the empty action list
fringe := [make_node(start_state, null, null)]
while fringe is not empty
    n := select and remove some node from the fringe
    for each action a applicable to n.state
        s := succ(n.state, a)
        n' := make_node(s, a, n)
        if s is a goal state, return n'.actionListFromRoot()
        add n' to fringe
return failure

Checking at expansion time:

fringe := [make_node(start_state, null, null)]
while fringe is not empty
    n := select and remove some node from the fringe
    if n.state is a goal state return n.actionListFromRoot()
    for each action a applicable to n.state
        add make_node(succ(n.state, a), a, n) to fringe
return failure

Breadth-First Search

Strategy: expand the shallowest unexpanded node. Implementation: The fringe is a FIFO queue.

For this search tree

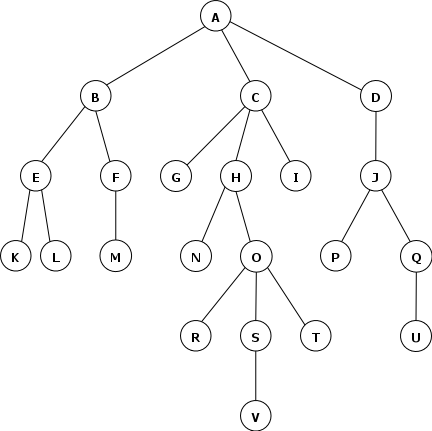
The queue evolves like this

    A
    B C D
    C D E F
    D E F G H I
    E F G H I J
    F G H I J K L
    G H I J K L M
    H I J K L M
    I J K L M N O
    J K L M N O
    K L M N O P Q
    L M N O P Q
    M N O P Q
    N O P Q
    O P Q
    P Q R S T
    Q R S T
    R S T U
    S T U
    T U V
    U V
    V

That is, the order of generation is ABCDEFGHIJKLMNOPQRSTUV and the order of expansion is the same.

If the goal nodes were M, V, and J, Breadth-First search would find J, the shallowest.

BFS

is complete (if $b$ is finite)
is optimal if all path costs are the same (because it always finds the shallowest node first)
Time complexity (worst case, goal at rightmost end of level $d$):
- Test at generation: $1 + b + b^2 + ... + b^d = O(b^d)$
- Test at expansion: $1 + b + b^2 + ... + b^d + (b^d-1)b = O(b^{d+1})$
Space complexity is same as time complexity because every node has to say in memory. (Why?) That’s right: EXPONENTIAL SPACE.

Depth-First Search

Strategy: expand the deepest unexpanded node. Implementation: The fringe is a LIFO queue (stack)

For the search tree above:

A
B C D
E F C D
K L F C D
L F C D
F C D
M C D
C D
G H I D
H I D
N O I D
O I D
R S T I D
S T I D
V T I D
T I D
I D
D
J
P Q
Q
U

Exercise: Give the order of generation and the order of expansion for this example.

If the goal nodes were M, V, and J, the Depth-First search above would find M.

DFS

is not complete (because of infinite depth and loops)
is not optimal
Time complexity (worst case: solution is at m): O(b^m) — regardless of whether we test at generation or expansion time. (Why?)
- If $m \geq d$, that sucks
- Can be better than BFS for dense solution space
Space complexity is $O(bm)$ — linear space

Depth-Limited Search

This is just a depth-first search with a cutoff depth. Here is the algorithm (for the test-at-expansion-time case)

fringe := [make_node(start_state, null, null)]
reached_limit := false
while fringe is not empty
    n := fringe.pop()
    if n.state is a goal state return n.actionListFromRoot()
    if n.depth == limit
        reached_limit := true
    else
        for each action a applicable to n.state
            fringe.push(make_node(succ(n.state, a), a, n))
return reached_limit ? cutoff : failure

DLS

Won’t run forever unless $b$ is infinite
is not complete because a goal may be below the cutoff
is not optimal
Time complexity (worst case: every path reaches cutoff): $O(b^c)$ — regardless of whether we test at generation or expansion time. (Why?)
Space complexity is $O(bc)$ — linear space.

Depth-First Iterative Deepening

Algorithm:

for i in 1..infinity
    run DLS to level i
    if found a goal at level i, return it immediately

DFID

is complete for finite b
is optimal in terms of the solution depth (and optimal in general if path cost is non-decreasing function of depth)
has asymptotic time complexity $O(b^d)$ in the worst case, ironically better than that of plain depth-first search!
has very modest memory requirements $O(bd)$ if expansion-based or $O(d)$ if backtracking-based.
generates fewer nodes than the version of BFS that checks for goals at expansion time
is asymptotically optimal in terms of time and space among brute-force tree searches that find optimal solutions!

Exercise: Show that the number of nodes generated by DFID is less than $b^d(\frac{1}{(1-\frac{1}{b})^2})$.

Uniform Cost Search

Strategy: Expand the lowest cost node. Implementation: the fringe is a priority queue: lowest cost node has the highest priority. In order to be optimal, must test at expansion, not generation, time.

Backwards Chaining

Run the search backwards from a goal state to a start state. Obiously this works best when the actions are reversible, and the set of goal states is small.

Bidirectional Search

Run a search forward from the start state and simulatneously. Motivation is that $b^{\frac{d}{2}} + b^{\frac{d}{2}}$ is much, much less than $b^d$. Works best when the backwards search is feasible. Problem is space complexity: one of the trees has to be kept in memory so we can test membership for a node generated in the other tree.