Foundations of Mathematics

Wait What is Math?
You’re not going to find an official definition of mathematics that everyone will agree on, but most people agree that it involves reasoning about quantity, change, structure, chance, causality, and space by both (1) finding abstract patterns and (2) creating models. Math aims to help us (1) both explain real phenomena and (2) discover truths that transcend the physical world. It’s such a well-known human activity that Wikipedia has an article on it!
Where does it come from?
Hmmm, well, no one knows for sure, but there’s a great book on the topic that might be right. If you look at the evolution of life and consciousness you might get some ideas. The earliest life forms that needed to move toward their food probably randomly bumped into food and survived. Natural selection likely led to sensing abilities enabling organisms to move toward the food. Next, lifeforms capable of making “models of their surroundings” so they could swerve around obstacles and remember where the food was, gained an evolutionary advantage.
This may explain how everyone can make models, and hence do Math!
Was it invented or discovered?
This question has been asked millions of times. Seriously.
The answer is probably both!
The question is so popular we can even question the question:

Whatever your take on this question is, Math has proven to be unreasonably effective in the natural sciences.
What are some of its branches?
Math is a big field of study. Here’s how Wikipedia breaks it down (this is just one way, and it’s not going to please everyone):
| Branch | Topics |
|---|---|
| Foundations | Philosophy of Mathematics • Mathematical Logic • Information Theory • Set Theory • Type Theory • Category Theory |
| Algebra | Abstract • Commutative • Elementary • Group Theory • Linear • Multilinear • Universal • Homological |
| Analysis | Calculus • Real Analysis • Complex Analysis • Hypercomplex Analysis • Differential Equations • Functional Analysis • Harmonic Analysis • Measure Theory |
| Discrete | Combinatorics • Graph Theory • Order Theory • Combinatorial Game Theory |
| Geometry | Algebraic • Analytic • Differential • Discrete • Euclidean • Finite |
| Number Theory | Arithmetic • Algebraic Number Theory • Analytic Number theory • Diophantine Geometry |
| Topology | General • Algebraic • Differential • Geometric • Homotopy Theory |
| Applied | Control theory • Operations Research • Probability • Statistics • Game Theory |
Another organization of topics can be found at Quanta Magazine’s Map of Mathematics. There’s also a cool Map of Mathematics video by Dominic Walliman, from which this poster can be found:
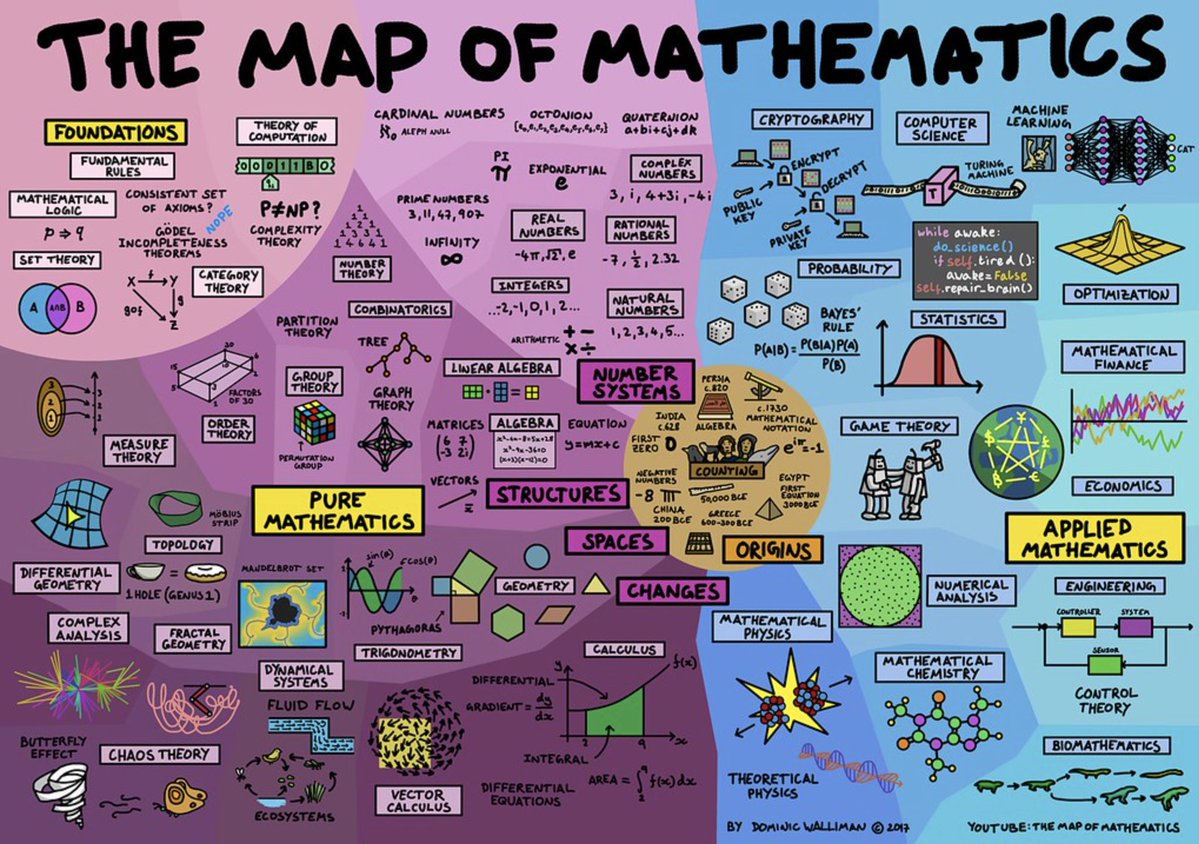
Why study foundations?
Good question! Many mathematicians don’t pursue a deep understanding of the foundations of math because they don’t need it in their daily work. But the field turns out to be really useful for computation, theoretical computer science, formal verification of program correctness (used in computer security), and proving complex theorems with the aid of a computer. In other words, it’s important for computer science, particularly in the study of programming languages.
What is page about?
This page is a light, very incomplete, sketch of topics within the area of the foundations of mathematics, focusing on the application of the concepts. There’s also a bit on numbers, too, since they play a role in foundations. The topics here are chosen because they are useful in theoretical computer science.
A Note About NotationMathematical reasoning benefits from concise, symbolic notation. It wasn’t always this way—until the 17th century or so math was mainly done in prose. Today we have some widely accepted notation for mathematical ideas, but there is still a surprising amount of variation. In fact, you are free to choose your own notation, as long as you are consistent.
Foundational Theories
There are many theories within mathematics. But there are three kinds of theories that can be viewed as providing a “foundation” for (all of) math: set theories, type theories, and category theories.
See the Wikipedia page on Foundations of Mathematics and the SEP article on Philosophy of Mathematics for a history of the subject.
Here is a table that Chat GPT helped me write:
| Set Theory | Type Theory | Category Theory | |
|---|---|---|---|
| Philosophy and Approach | Math is about classifying elements by putting them into sets. Everything is a set or an element of a set. Set theory requires logic (generally a classical one) to already exist. | Math is about types that allow you to construct terms that inhabit those types. All objects have a type. Logic emerges from the theory. Usually constructive in nature (though classical type theories do exist). Concerned more with evidence than truth. | Math is about structures and the relationships between them, without worrying about internal details. |
| Key Features | Sets are built up from smaller sets, with rules to avoid paradoxes. Pretty much everything is a set, which is both a strength and a weakness. | Terms have types. Types can depend on other types as well as on terms. Propositions are types. Proofs are programs. | Categories have objects and morphisms (arrows or relationships). Functors map between categories. Commutative diagrams are used a lot. |
| Concepts | Elements, membership, subsets, power sets, tuples, sequences, partitions, relations, equivalence relations, orders, cardinality. | Types, terms, inductive types, sums ($+$), products ($\times$), dependent types ($\Pi$ and $\Sigma$), propositions as types, proofs as programs, equality types, universes. | Objects, morphisms, functors, natural transformations, limits, colimits, adjunctions, monads, categories, monoids, topoi. |
| Characteristic Notation | $x \in S$ means $x$ is an element of set $S$. | $x : A$ means the term $x$ is of type $A$. | $X \xrightarrow{f} Y$ means $f$ is a morphism from category $X$ to category $Y$. |
| Applications | Used pretty often, kind of assumed you know it. | Computer science, formal verification, proof assistants. | Abstract algebra, topology, geometry, mathematical logic. |
| Exemplars | Some set theories are: ZF and ZFC, NBG, NF and NFU, MK, KP, CST. | Some type theories are: Simply-Typed $\lambda$ calculus, MLTT, System F, DTT, CoC, HoTT. | Some category theories are: ETCS, Topos Theory, Abelian, Monoidal. |
Math and LogicMath and logic are related, but not the same thing. Mathematicians do quite a lot of logic. If interested, I have more extensive notes that get into logic in more detail, with coverage of non-bivalent, intuitionistic, paraconsistent, fuzzy, non-monotonic and a bunch of other types of logic. They get into metalogical notions of soundness and completeness, too.
Individuals
In math, we are interested in objects and the relationships between them. The most primitive objects are called atoms, or individuals. Examples include 5, $\pi$, a, b, California, Chennai, Juneau, 🧶, Neptune, Zeus, false, and Minnie Mouse.
In Set Theory, individuals are just assumed to already exist. Actually it’s weird: many set theories (including the most popular one, ZFC) don’t even have individuals: they make everything a set! But some set theories have them, and call them urelements.
In Type Theory, we first create a type then define rules to populate the types. These definitions bring the individuals into existence. Here is a definition of the type $\textsf{nat}$ of natural numbers:
We’ll use $1$ for $s0$, $2$ for $ss0$, $3$ for $sss0$ and so on. Because we can!
Here is the type $\textsf{bool}$:
Here is a type for binary trees of natural numbers:
Tuples
Objects such as $()$, $(21,3)$, $(a,a,b,a,b,a,b,b)$, or $(do, re, mi, fa, so, la, ti, do)$ are called tuples. Sometimes they are called sequences. The elements of a tuple are ordered. Given a tuple $t$, you access the $i$th element with the notation $\:t\!\downarrow\!i$. You can start with $0$ or $1$. I like to start with $0$.
Examples: Let $\,t = (8, F, (2,5))$. Then:
| $t\!\downarrow\!0 = 8$ |
| $t\!\downarrow\!1 = F$ |
| $t\!\downarrow\!2 = (2,5)$ |
| $t\!\downarrow\!3\;$ has no value |
Please note that $(a,(a,a))$ is not the same thing as $((a,a),a)$.
In Type Theory, the type of two-element tuples, also called pairs, whose first element has type $A$ and the second has type $B$ is the product type $A \times B$:
Tuples can be generalized to have any number of components, even 0:
A tuple with $n$ components is called an $n$-tuple. The special value $()$, the one and only $0$-tuple, has its very own type, called unit:
Sequences can be concatenated. If $t_1$ is an $m$-tuple and $t_2$ is an $n$-tuple then $t_1 • t_2$ is an $(m+n)$-tuple:
| $(a_1, \ldots, a_m) • (b_1, \ldots, b_n) = (a_1, \ldots, a_m, b_1, \ldots, b_n)$ |
We do not bother distinguishing one-element tuples from the contained element, that is, $a = (a)$. So it is fine to say $(a,b) • c = (a,b,c)$, and even $a • b = (a,b)$.
In Set Theory, tuples are constructed rather unnaturally. We’ll see how later.
Sets
A set is an unordered collection of unique elements. Sets model properties of things. To say that $x$ is a member of the set $S$ means that $x$ has a certain property (the property expressed by the set).
Examples:
Membership
This is perhaps the most fundamental notion of set theory.
| $x \in A \textrm{ means } x \textrm{ is a member of set } A$ |
| $x \notin A \textrm{ means } \neg (x \in A)$ |
Examples:
| $3 \in \mathbb{N}$ |
| $\textrm{Manitoba} \notin \textrm{AustralianStates}$ |
What does it mean to be a member? It can vary.
- For crisp sets, you’re either in or you’re out. No in-between. This is the most common kind of set.
- For fuzzy sets, membership can be partial. For example, you might be 0.8 in the set of tall people.
Comprehension
We can write a set by describing its characteristic property. This form is called a set comprehension. Examples:
Avoiding Paradoxes
Comprehension is not unrestricted! You cannot just make stuff up when using a set comprehension. Not everything you can write is a set. In particular, $\{x \mid x \notin x\}$ is not considered to be a set. Do you see why? Call that set $r$ and ask whether $r \in r$. Oops! Nice antinomy!
Different set theories avoid the paradox in different ways. Some theories make self-containing sets impossible to write. NF allows such sets but gets around the root problem with stratification. NBG distinguishes sets and classes. Somehow or another, what is and what is not a set requires a rigorous definition.
Some Famous Sets
Here are some sets that are universally used in the world of math:
Set Operators
Definitions:
| $A \subseteq B$ | $=$ | $\forall x. x \in A \supset x \in B$ | (subset of) |
| $A = B$ | $=$ | $A \subseteq B \wedge B \subseteq A$ | (equal to) |
| $A \neq B$ | $=$ | $\neg (A = B)$ | (not equal to) |
| $A \cup B$ | $=$ | $\{x \mid x \in A \vee x \in B \}$ | (union) |
| $A \cap B$ | $=$ | $\{x \mid x \in A \wedge x \in B \}$ | (intersection) |
| $A \setminus B$ | $=$ | $\{x \mid x \in A \wedge x \notin B\}$ | (minus (alt. $A - B$)) |
| $A \vartriangle B$ | $=$ | $(A \cup B) \setminus (A \cap B)$ | (symmetric difference (alt. $A \ominus B$)) |
| $A \times B$ | $=$ | $\{(x,y) \mid x \in A \wedge y \in B\}$ | (cross product) |
| $\mathcal{P}(A)$ | $=$ | $\{P \mid P \subseteq A\}$ | (powerset) |
| $\bigcup A$ | $=$ | $\{x \mid x \in P \textrm{ for some } P \in A\}$ | (union) |
| $\bigcap A$ | $=$ | $\{x \mid x \in P \textrm{ for all } P \in A\}$ | (intersection) |
| $A^n$ | $=$ | $\{ (a_1, \ldots, a_n) \mid n \geq 0 \wedge \forall i. a_i \in A \}$ | (n-element sequence) |
| $A^*$ | $=$ | $\bigcup_{i \geq 0}\,A^i$ | (sequence) |
Examples: Let $A = \{a, b, c\}$ and $B = \{b, f\}$. Then:
| $A \cup B = \{a, b, c, f\}$ |
| $A \cap B = \{b\}$ |
| $A \setminus B = \{a, c\}$ |
| $A \vartriangle B = \{a, c, f\}$ |
| $A \times B = \{(a,b), (a,f), (b,b), (b,f), (c,b), (c,f)\}$ |
| $B^1 = B = \{b, f\}$ |
| $B^2 = B \times B = \{(b,b), (b,f), (f,b), (f,f)\}$ |
| $B^3 = B \times B \times B = \{(b,b,b), (b,b,f), (b,f,b), (b,f,f), (f,b,b), (f,b,f), (f,f,b), (f,f,f)\}$ |
| $\mathcal{P}(B) = \{\varnothing, \{b\}, \{f\}, \{b,f\}\}$ |
| $(6, T, 7.3) \in \mathbb{N} \times \mathbb{B} \times \mathbb{R}$ |
| $(2, 3, 8) \in \mathbb{N}^3$ |
| $\{a,b\}^* = \{(), a, b, (a,a), (a,b), (b,a), (b,b), (a,a,a), \ldots\}$ |
Tuples in Set Theory
In everyday math and computer science, sets are unordered collections of unique elements; tuples are ordered and can have duplicates. Completely different beasts.
We saw how to make tuples in Type Theory earlier. How are they treated in Set Theory?
Well, in Set Theory, everything comes from sets, so there are mechanisms to define tuples as sets, and even numbers as sets. A set theorist would say that $(x,y)$ “is” the set $\{ x, \{x,y\} \}$. But don’t worry about it. Take the everyday approach and decree that tuples are a distinct primitive mathematical construct.
Tuples in Set Theory are weirdWeird indeed! With $(5, 3)$ being $\{ 5, \{5, 3\}\}$, we have $5 \in (5,3)$ but $3 \not\in (5,3)$. Wat.
Disjointness and Partitions
Sometimes we want to separate out the elements of a set into non-overlapping groups. Two concepts are useful here.
$A$ and $B$ are disjoint iff $A \cap B = \varnothing$
$\Pi = \{P_1, P_2, \ldots, P_n\} \subseteq \mathcal{P}(A)$ is a partition of $A$ iff:
- $\varnothing \notin \Pi$
- $\forall x\:i\:j. (x \in P_i \wedge i \neq j) \supset x \notin P_j$
- $\bigcup \Pi = A$
Example: $\{ \textrm{EVEN}, \textrm{ODD} \}$ is a partition of $\mathbb{Z}$.
Some Set Theorems
Assuming you already know first-order classical logic, you can use the definitions above to prove some interesting theorems about sets. The following are theorems in any of the major set theories (ZFC, NFU, etc.):
| $A \cup A = A$ | (idempotency) |
| $A \cap A = A$ | (idempotency) |
| $A \cup B = B \cup A$ | (commutativity) |
| $A \cap B = B \cap A$ | (commutativity) |
| $A \cup (B \cup C) = (A \cup B \cup C)$ | (associativity) |
| $A \cap (B \cap C) = (A \cap B \cap C)$ | (associativity) |
| $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ | (distributivity) |
| $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ | (distributivity) |
| $A \cup (A \cap B) = A$ | (absorption) |
| $A \cap (A \cup B) = A$ | (absorption) |
| $A \setminus (B \cup C) = (A - B) \cap (A - C)$ | (DeMorgan) |
| $A \setminus (B \cap C) = (A - B) \cup (A - C)$ | (DeMorgan) |
| $\varnothing \subseteq A$ |
| $A \subseteq A$ |
| $A \subseteq A \cup B$ |
| $A \cap B \subseteq A$ |
| $A \cup \varnothing = A$ |
| $A \cap \varnothing = \varnothing$ |
| $A \setminus \varnothing = A$ |
| $\varnothing \setminus A = \varnothing$ |
| $A \subseteq B \Leftrightarrow A \cup B = B$ |
| $A \subseteq B \Leftrightarrow A \cap B = A$ |
| $A \subseteq B \supset A \cup C \subseteq B \cup C$ |
| $A \subseteq B \supset A \cap C \subseteq B \cap C$ |
| $A \times \varnothing = \varnothing$ |
| $A \times (B \cup C) = (A \times B) \cap (A \times C)$ |
| $A \times (B \cap C) = (A \times B) \cap (A \times C)$ |
| $(A \times B) \cap (C \times D) = (A \cap C) \times (B \cap D)$ |
| $(A \times B) \cup (C \times D) \subseteq (A \cup C) \times (B \cup D)$ |
Relations
A relation is a subset of a cross product. That’s it. That’s the whole definition.
For the relation $R \subseteq A \times B$, we say $A$ is the domain and $B$ is the codomain. If $(a,b) \subseteq R$ we write $aRb$. The inverse $R^{-1} \subseteq B \times A$ is $\{(b,a) \mid aRb\}$.
Examples:
| $\leq\;\subseteq \mathbb{N} \times \mathbb{N}$, and $(5,7) \in\;\leq$, so we can write $5 \leq 7$. |
| If $R = \{ (1,2), (3,4), (5, 5), (6,7) \}$ then $R^{-1} = \{ (2,1), (4,3), (5,5), (7,6) \}$. |
Note that because a relation is a subset of $A \times B$, the set of all relations over $A$ and $B$ is $\mathcal{P}(A \times B)$.
For $R \subseteq A \times A$ we define:
- $R$ is reflexive iff $\forall a. aRa$
- $R$ is irreflexive (a.k.a anti-reflexive) iff $\forall a. \neg aRa$
- $R$ is symmetric iff $\forall a\:b. aRb \supset bRa$
- $R$ is asymmetric iff $\forall a\:b. aRb \supset \neg bRa$
- $R$ is antisymmetric iff $\forall a\:b. aRb \wedge bRa \supset a=b$
- $R$ is transitive iff $\forall a\:b. aRb \wedge bRc \supset aRc$
- $R$ is total iff $\forall a\:b. aRb \vee bRa$
More definitions:
- $R$ is an equivalence relation iff it is reflexive, symmetric, and transitive
- $R$ is a partial order iff it is reflexive, antisymmetric, and transitive
- $R$ is a total order iff it is asymmetric, transitive, and total
If $R \subseteq A \times B$ and $S \subseteq B \times C$ then the composition of $R$ and $S$ is $S \circ R$ = $\{(a,c) \mid \exists b. aRb \wedge bSc\}$.
Example:
Let $R = \{(1,2),(2,5),(1,1)\}$ and $S = \{(5,10),(2,8),(9,2)\}$. Then:
- $R \circ S = \{(9,5)\}$
- $S \circ R = \{(1,8), (2,10)\}$
Even though relations are sets, the superscript notation on relations means something different than it does for regular sets. This seems infuriating until you realize that math notation is very contextual and changes depending on what you are talking about. Anyway, here is what the superscripts mean for relations:
| $R^2 = \{ (a,b) \mid \exists c. aRc \wedge cRb \}$ |
| $R^3 = \{ (a,b) \mid \exists c. \exists d. aRc \wedge cRd \wedge dRb \}$ |
| $R^4 = \{ (a,b) \mid \exists c. \exists d. \exists e. aRc \wedge cRd \wedge dRe \wedge eRb \}$ |
| $\ldots$ |
| $R^* = \bigcup_{i \geq 0}\,R^i$ |
Those definitions imply $R^2 = R \circ R$, $R^3 = R \circ R \circ R$, and so on.
These forms turn out to be very useful in computation theories, as we frequently use relations that represent a single computation step, so the * form of the relation will mean any number of steps.
Example:
Let $\;\longmapsto\;= \{ (x,y) \mid y = 2x\}$. Then:
| $5 \longmapsto 10$ | (one step) |
| $5 \longmapsto^2 20$ | (two step) |
| $8 \longmapsto^3 64$ | (three step) |
| $2 \longmapsto^* 131072$ | (any number of steps 🤯) |
Ambiguous Notation AlertAgain, $R^2$ is ambiguous, because since a relation is a set, $R^2$ could mean $R \times R$, but it is much more common to interpret it as $R \circ R$. You should probably supply context when talking about this stuff.
Functions
A function maps an input to an output, such that given any input (called the argument), you get the same output every time you apply the function.
In Type Theory, functions are basic objects, so they have types. The type of a function whose input is $A$ and whose output is $B$ is the type $A \rightarrow B$. We define a function by providing an expression that produces the result of applying the function. Examples:
| $(\lambda x. x^2 - x + 5)\!:(\mathsf{int \rightarrow int})$ |
| $(\lambda n. n \log_2 n)\!:(\mathsf{nat \rightarrow real})$ |
| $(\lambda x. x \bmod 2 = 0)\!:(\mathsf{nat \rightarrow bool})$ |
| $(\lambda x. \lambda y. 5x + 2y - 7)\!:(\mathsf{real \rightarrow real \rightarrow real})$ |
| $(\lambda (x, y). 5x + 2y - 7)\!:(\mathsf{real \times real \rightarrow real})$ |
| $(\lambda \theta. \lambda (x, y). (x \cos\theta - y \sin\theta, x\sin\theta + y\cos\theta))\!:(\mathsf{real \rightarrow (real \times real) \times (real \times real)})$ |
It is customary to show the types of the parameter and the body. You can attach the types with a colon or to save space you can make the types as subscripts:
| $\lambda x\!:\!\textsf{int}. (x^2 - x + 5)\!:\!{\textsf{int}}$ |
| $\lambda x_{\small \textsf{int}}. (x^2 - x + 5)_{\small \textsf{int}}$ |
| $\lambda n_{\small \textsf{nat}}. (n \log_2 n)_{\small \textsf{real}}$ |
| $\lambda x_{\small \textsf{nat}}. (x \bmod 2 = 0)_{\small \textsf{bool}}$ |
| $\lambda x_{\small \textsf{real}}. \lambda y_{\small \textsf{real}}. (5x + 2y - 7)_{\small \textsf{real}}$ |
| $\lambda (x, y)_{\small \mathsf{real} \times \mathsf{real}}. (5x + 2y - 7)_{\small \textsf{real}}$ |
| $\lambda \theta_{\small \mathsf{real}}. \lambda (x, y)_{\small \mathsf{real} \times \mathsf{real}}. (x \cos\theta - y \sin\theta, x\sin\theta + y\cos\theta)_{\small \mathsf{real} \times \mathsf{real}}$ |
Often the type of the function can be inferred from context, in which case we can leave off the type annotations. Things may look “untyped” but they’re not, as long as you can infer them. If you can’t infer them, write them down!
| $\lambda x. x^2 - x + 5$ |
| $\lambda n. n \log_2 n$ |
| $\lambda x. x \bmod 2 = 0$ |
| $\lambda x. \lambda y. 5x + 2y - 7$ |
| $\lambda (x, y). 5x + 2y - 7$ |
| $\lambda \theta. \lambda (x, y). (x \cos\theta - y \sin\theta, x\sin\theta + y\cos\theta)$ |
The typing rule for functions is simple:
Here’s a fun one. What is the type of $\lambda f. \lambda x. f(f(x))$?
Well, $(\textsf{int} \rightarrow \textsf{int}) \rightarrow \textsf{int} \rightarrow \textsf{int}$ works.
But so does $(\textsf{real} \rightarrow \textsf{real}) \rightarrow \textsf{real} \rightarrow \textsf{real}$. And so does $(\textsf{bool} \rightarrow \textsf{bool}) \rightarrow \textsf{bool} \rightarrow \textsf{bool}$. And so on. We can generalize the type by introducing type variables.
The type is $\forall \alpha. (\alpha \rightarrow \alpha) \rightarrow \alpha \rightarrow \alpha$. You don’t have to write the $\forall$ though. But it is a nice way to say, “you can substitute any type you like for the type variable $\alpha$.”
Functions are sets in Set Theory
In set theory, a function $f \subseteq A \times B$ is just a relation in which every element of $A$ appears exactly once as the first element of a pair in $f$.
If $f$ is a function and $(a,b) \in f$ we write $f a = b$, or $f(a) = b$, and say $b$ is the value of $f$ at $a$. The range of $f$ is $\{b \mid \exists a. b = f a\}$.
The set of all functions from $A$ to $B$ is denoted $A \rightarrow B$. Looks just like the type theory notation! Though set theorists sometimes write $B^A$.
Since functions are relations and therefore sets, we can write them in set notation, but it’s totally fine to use the $\lambda$ notation from Type Theory. It’s fine to share notation between theories!
| $\{...(-1,7), (0,8), (1,9), (2,10), ...\}$ |
| $\{(x, y) \mid x \in \mathbb{Z} \wedge y = x + 8\}$ |
| $\{(x, x+8) \mid x \in \mathbb{Z}\}$ |
| $\lambda x_\mathbb{Z} . x+8$ |
Note that sometimes we don’t make the domain explicit when we write functions. We often infer it from context.
Sets are functions in Type Theory
So how about this? If you start with Type Theory and you want sets, you can represent a set as a function returning a bool. Return $T$ if the input should be in the set and $F$ otherwise.
Example: The set $\{ x \mid x \bmod 2 = 0\}$ is the function $\lambda x. x \bmod 2 = 0$.
Basically the set $\{ x \mid e \}$ is really just $\lambda x. e$.
Also, the expression $x \in A$ is just $Ax$. Do you see why?
Some Syntax
While you could use nothing but lambdas everywhere, there are a bunch of forms that make things much easier to read. The first is the amazing let-notation:
- Example: $\;\mathsf{let}\;x=3\;\mathsf{in}\;x+5$ evaluates to $8$
- Because: $\;\mathsf{let}\;x=3\;\mathsf{in}\;x+5$ is the same as $(\lambda x . x+5)(3)$
- In general: $\;\mathsf{let}\;x=E\;\mathsf{in}\;E'$ is the same as $(\lambda x . E')(E)$
Where-notation
- Example: $\;x+5\;\mathsf{where}\;x=3$ evaluates to $8$
- Because: $\;x+5\;\mathsf{where}\;x=3$ is the same as $(\lambda x . x+5)(3)$
- In general: $\;E'\;\mathsf{where}\;x=E$ is the same as $(\lambda x . E')(E)$
If-notation:
- $\mathsf{if}\;b\;\mathsf{then}\;x\;\mathsf{else}\;y = \begin{cases} x & b = T \\ y & b = F\end{cases}$
Substitution:
- $f[b/a] = \lambda x. \mathsf{if}\;x=a\;\mathsf{then}\;b\;\mathsf{else}\;f(x)$
Function iteration:
- $f^0(x) = x$
- $f^1(x) = f(x)$
- $f^2(x) = f(f(x))$
- $f^3(x) = f(f(f(x)))$
- ...
- $f^{n+1}(x) = f(f^n(x))$
Ambiguous Notation AlertMany mathematicians purposefully blur the distinction between $\sin^2\theta$ and $(\sin \theta)^2$, leaving you, the poor reader, to figure out what they mean by context.
It appears that for trig functions, people tend to use the iterative form for the power form, but for other functions the iterative form usually means iteration? Maybe?
Don’t worry too much. It’s all a consequence of the fact everyone is allowed to invent their own notation. Just remember, all things are contextual.
Ambiguous Language AlertIf $f$ is a function, do not say “the function $f(x)$” unless the function $f$, when applied to $x$, actually yields a function. Also do not say things like “the function $n^2$” because $n^2$ is a number. The function you probably have in mind is $\lambda n. n^2$. That doesn’t stop people from abusing the notation, though.
The -jections
Time for more definitions! For $f: A \rightarrow B$:
- $f$ is a surjection (i.e., $f$ maps $A$ onto $B$) iff $\forall b. \exists a. f a = b$
- $f$ is an injection (i.e., $f$ maps $A$ one-to-one to $B$) iff $\forall a . \forall b. a \neq b \supset f a \neq f b$
- $f$ is a bijection, a.k.a. a one-to-one correspondence iff $f$ is a surjection and an injection

If $f$ is a bijection from $A$ to $B$, then:
- $f^{-1}$ is a bijection from $B$ to $A$
- $\forall a. f^{-1}(f\,a) = a$
- $\forall b . f(f^{-1}\,b) = b$
Partial Functions
We defined a function as a relation where every element of the domain appears exactly once as the first element of a pair. If we relax this to every element of the domain appearing at most once then we have a partial function. Think of a partial function as not being able to compute a value for every element, or one in which the value at some inputs is “undefined.”
The set of all partial functions from $A$ to $B$ is denoted $A \rightharpoonup B$.
If $f \in A \rightharpoonup B$ then:
- $f \in C \rightarrow B$ for some $C \subseteq A$, where $C$ is precisely the set of elements from $A$ at which $f$ is defined.
- $f \in A \rightarrow B \cup \{\bot\}$, where $\bot$ is a representation of the undefined value.
Partial functions are useful in computer science because they allow us to model programs that might not terminate or might throw an error.
If you are talking about partial functions, you might want to call out regular functions (that are defined at all points in the domain) as being total functions.
Maps
Sometimes it’s convenient to think of partial functions as maps where the inputs are the keys and the outputs are the values. When we do, we tweak the notation a bit. Here’s a partial function, $m \in \textsf{Unicode}^* \rightharpoonup \mathbb{N}$:
$(\lambda s. \bot)[1/\texttt{a}][2/\texttt{b}][3/\texttt{c}]$
The function substitution notation is perfect here, as it says that the value at every input is $\bot$ unless explicitly overwritten. But we said above that functions are just sets. Which set is this? We can say it’s this:
$\{ (\texttt{a}, 1), (\texttt{b}, 2), (\texttt{c}, 3) \} \cup \{ (s, \bot) \mid s \in \textsf{Unicode}^* \setminus \{\texttt{a}, \texttt{b}, \texttt{c}\} \}$
It’s a bit hard to read, though, so in these cases, we do better writing the function in map notation:
$\{ \texttt{a}\!: 1, \texttt{b}\!: 2, \texttt{c}\!: 3 \}$
We will consider the latter just syntactic sugar for the former, rather than defining maps as a primitive type. So don’t forget, because maps are just functions, the substitution notation works for them too. If $m$ is the map above, we can write things like $m[4/\texttt{d}]$ for the map just like $m$ with the additional key-value pair mapping $d$ to $4$, and $m[0/\texttt{b}]$ for the map like $m$ except $\texttt{b}$ now maps to $0$.
Numbers
Numbers are so useful. They are the way we capture quantity and dimension.
We saw how to define the natural numbers in Type Theory earlier. In Set Theory, numbers are, um, sets. The natural numbers are defined like this: $0 = \varnothing$, $1 = \{ 0 \}$, $2 = \{ 0, 1 \}$, $3 = \{ 0, 1, 2 \}$, etc. That does mean that $2 \in 3$ which is weird but ok. In these notes, we’re going to be pragmatic and distinguish numbers from sets. Remember there’s a difference between being in the would of foundations and doing your everyday work.
Here are some famous sets of numbers from set theory:
| Kind | Symbol | Notes |
|---|---|---|
| Natural Numbers | $\mathbb{N}$ | $\{0, 1, 2, 3, \ldots\}$ |
| Integers | $\mathbb{Z}$ | $\{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}$ |
| Rational Numbers | $\mathbb{Q}$ | $\{\frac{a}{b} \mid a, b \in \mathbb{Z} \wedge b \neq 0\}$ |
| Real Numbers | $\mathbb{R}$ | (See the Wikipedia article) |
| Complex Numbers | $\mathbb{C}$ | Has 2 real components, written ($a+bi$) |
| Quaternions | $\mathbb{H}$ | Has 4 real components, written ($a+bi+cj+dk$) |
| Octonions | $\mathbb{O}$ | 8 real components, with units $e_0 ... e_7$ |
| Sedenions | $\mathbb{S}$ | 16 real components |
In set theory, sets of numbers can be subsets of each other. For example, the integers can be defined as $\mathbb{Z} = \mathbb{N} \cup \{-n \mid n \in \mathbb{N}\}$.
Did you know about algebraic vs. transcendental numbers? This amazing diagram by Keith Enevoldsen shows how they fit in:
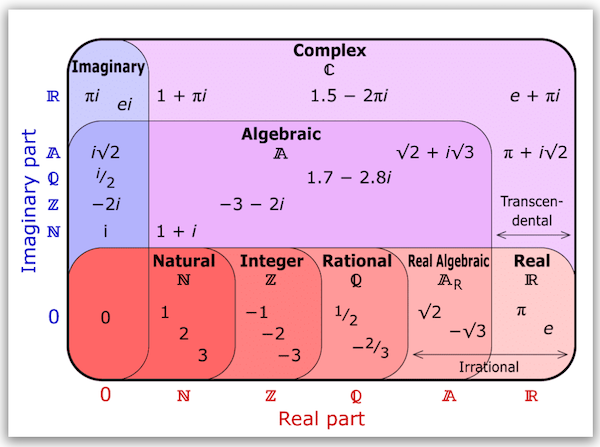
Things get interesting when you go beyond the reals. What isn’t “real” by the way? Imaginary perhaps? Not a good name, as Jade shows:
Operations
For natural numbers:
- Addition: $x^{(1)}y = x + y = \underbrace{\:s\: \ldots \:s\:}_{y}\;x$
- Multiplication: $x^{(2)}y = x \times y = \underbrace{\:x + x + \ldots + x\:}_{y}$
- Exponentiation: $x^{(3)}y = x \uparrow y = \underbrace{\:x \times x \times \ldots \times x\:}_{y}$
- Tetration: $x^{(4)}y = x \uparrow\uparrow y = \underbrace{\:x \uparrow x \uparrow \ldots \uparrow x\:}_{y}$ (also called hyper4 or power-tower)
- Pentation: $x^{(5)}y = x \uparrow\uparrow\uparrow y = \underbrace{\:x \uparrow\uparrow x \uparrow\uparrow \ldots \uparrow\uparrow x\:}_{y}$
- And on and on....
Addition, multiplication, and exponentiation work for real numbers too. There are also inverses:
- Subtraction: $x - y$ = the $z$ such that $y + z = x$
- Division: $x \div y$ = the $z$ such that $y \times z = x$
- Logarithm: $\log_y(x)$ = the $z$ such that $y^z = x$
- And there are “inverses” of the operators beyond exponentiation as well
Got all that? Do you have a good sense of these numbers and operations? Whether you do or don’t, watch Vi Hart’s piece:
Also important:
- The floor of a real number $x$, denoted $\lfloor x \rfloor$, is the largest integer less than or equal to $x$.
- The ceiling of a real number $x$, denoted $\lceil x \rceil$, is the smallest integer greater than or equal to $x$.
Cardinal Numbers
A cardinal number tells of how many of something there are. An ordinal number gives the position of something in an ordered sequence.
So how many elements are there in a given set? We’d need a cardinal number for that. In fact the number of elements in a set is called the cardinality of the set. The cardinality of set $A$ is denoted $|A|$ and obeys these axioms:
- $|A| = |B|$ iff there exists a bijection between $A$ and $B$. That is, for each element in $A$ there is a matching value in $B$ and vice-versa.
- $|A| \leq |B|$ iff there exists an injection from $A$ to $B$. That is, for each element of $A$ there is a matching element in $B$, but not necessarily vice-versa.
- $|A| < |B|$ iff $|A| \leq |B|$ and $|A| \neq |B|$
Did you notice something about bijections? They are important! They tell us when two sets are the same size, without having to count them. Matching is more fundamental than counting.
Think about this
Matching is more fundamental than counting. Imagine yourself without words for what we now call numbers. You could still come up with ideas of greater than or less than, and allocate resources, and even trade. Counting is an advanced concept!
AGAIN, MATCHING IS MORE FUNDAMENTAL THAN COUNTING.
If there exists a bijection between a set $A$ and the set $\{1, 2, ... k\}$ for some $k \geq 0$, we say that A is finite and that $|A| = k$. So for example:
- $|\varnothing| = 0$
- $|\{a, b, c\}| = 3$
- $|\{8, 7, \{6, 2, 4\}, 3, \textsf{true} \}| = 5$
- $|\{\varnothing\}| = 1$
But what about $\mathbb{N}$? We can’t find a bijection between that and $\{1, 2, ... k\}$ for any natural number $k$. That set must not be finite.
Infinity
A set is infinite iff there is a bijection between it and a proper subset of itself. A set is finite iff it is not infinite.
So there are just as many even numbers as there are natural numbers. Here’s a video explanation, together with some additional historical context:
Okay so what is the cardinality of $\mathbb{N}$?
We define it to be $\aleph_0$. This is a cardinal number. Not a natural number, but definitely a cardinal, because it tells you how many of something there is. In principle you can count, or at least list, all the natural numbers. The list will go on literally forever, but if you had forever, you would get them.
A set $A$ is countable (a.k.a. listable) iff $A$ is finite or $|A| = \aleph_0$.
Examples:
| $| \varnothing | = 0$ |
| $| \{a, b, c\} | = 3$ |
| $| \{8, 7, \{6, 2, 4\}, 3\} | = 4$ |
| $| \{\varnothing\} | = 1$ |
| $| \mathbb{Z} | = \aleph_0$ |
$\mathbb{Z}$ is countable because $\lambda n.(\textsf{if}\;\textit{even}(n)\;\textsf{then}\;\frac{-n}{2}\;\textsf{else}\;\frac{n+1}{2})$ is a bijection from $\mathbb{N}$ to $\mathbb{Z}$.
$\mathbb{N} \times \mathbb{N}$ is countable, too:
(0,0) (0,1) (1,0) (0,2) (1,1) (2,0) (0,3) (1,2) (2,1) (3,0) (0,4) (1,3) (2,2) (3,1) (4,0) (0,5) (1,4) (2,3) (3,2) (4,1) (5,0) ...
By a similar argument, $\mathbb{Q}$, $\mathbb{N}^i$, and any countable union of countable sets are all countable.
Here’s Vi Hart again, if you want to see more about these infinities:
You can keep going on and on with these infinities, thanks to the power of the power set.
Cantor’s Theorem: For any set $A$, $|A| < |\mathcal{P}(A)|$. Proof: Clearly $|A| \leq |\mathcal{P}(A)|$, so we only have to show $|A| \neq |\mathcal{P}(A)|$. Proceed by contradiction. Assume $|A| = |\mathcal{P}(A)|$, which means there is a function $g$ mapping $A$ onto $\mathcal{P}(A)$. Consider $Y = \{x \mid x \in A \wedge x \notin g(x)\}$. Since $g$ is an onto function, there must exist a value $y \in A$ such that $g(y)=Y$. If we assume $y \in Y$ then by definition means that $y \notin Y$. But if we assume $y \notin Y$, then that means $y \in Y$. This is a contradiction, so the assumption that a surjectve $g$ exist cannot hold. Therefore $|A| \neq |\mathcal{P}(A)|$. Slay.
Similar arguments to this proof of Cantor’s theorem show that the following sets are uncountable:
- $\{x \mid x \in \mathbb{R} \wedge 0 < x < 1\}$
- $\mathbb{N} \rightarrow \mathbb{N}$
Fun fact. Okay so $\{x \mid x \in \mathbb{R} \wedge 0 < x < 1\}$ is uncountable. But is its cardinality equal to, or strictly less than, $\mathbb{R}$ itself? Turns out it’s equal! The bijection you are looking for is: $\lambda x. \frac{1}{\pi}tan^{-1}x + \frac{1}{2}$ is a bijection to $<0,1>$.
The fact that $\mathbb{N}\rightarrow\mathbb{N}$ is uncountable means that there are functions for which no computer program can be written to solve, because programs are strings of symbols from a finite alphabet and thus there are only a countably infinite number of them.
Notable Numbers
Don’t miss Robert P. Munafo’s numbers pages.
Big Numbers
Don’t miss Robert P. Munafo’s big numbers pages.
Seriously, don’t miss it!
Bigger and Bigger and Bigger
Vsauce takes us through lots of lots of infinities and more! After this video you will know the difference between cardinals and ordinals.
Foundations and Computation
Much of mathematics is aided by the use of computers. Computers speed up time, allowing us to think previously unthinkable thoughts. Science and mathematics are qualitatively different with the augmentation and amplification of human thought. In math, complex proofs can be found, or at least checked, by an automated proof assistant. Generally, these proof assistants are based on Type Theory, not Set Theory, for various reasons (many taken from these slides by Sergey Goncharov):
- In Type Theory, functions are primitive. They are not just special kinds of sets of pairs. Functions compute things, and thus feel dynamic. Why look at them like static relations?
- Set Theory purports to be simpler, in that it has fewer basic notions, as in everything is a set. But this really isn’t the case, as the axioms of Set Theory are really complex and few people know them all. The axioms are arguably arbitrary and don’t help much in finding proofs. Set Theory is just too theoretical.
- Set Theory’s “everything is a set” approach is actually too simple. We want to distinguish tuples and functions and relations and numbers. Mathematicians naturally think in terms of different types of objects. Why treat them all as sets? This leads to silliness like $2 \in 3$ and $\pi \cap \mathbb{R}$.
- In Set Theory, logic and objects come first, then we use sets to group the objects. In type theory, types come first, then we construct objects to inhabit the types, and logic emerges. Thus Type Theory does not decouple logic from the structures it defines the way Set Theory does.
- Most type theories are constructive! There’s no excluded middle, for one thing. To prove existentials, you have to supply a witness. To prove disjunctions, you have to show one of the disjuncts. Computation feels constructive. In contrast, most set theories are classical.
- Set Theory’s underlying logic has debatable principles such as the Excluded Middle, the Axiom of Choice, and Impredicativity, which get in the way of automation.
Beyond Foundations
This page is focused on foundations. But there’s much more to math that is useful in computer science. You might want to check out:
- Counting principles (pigeonhole, addition, multiplication)
- Permutations
- Combinations
- Probability, for which you really need to see the amazing Seeing Theory: A Visual Introduction to Probability and Statistics
- Recurrence Relations
- Type Theory
- Category Theory
- Information Theory
- Algebraic Structures
- Linear Algebra
- Geometry
- Topology
- Analysis
- Formal Proofs
- Numerical Analysis
- Optimization
Does Math Describe the World?
Did you watch the Vsauce video above? Kind of cool how Michael says we can do math that isn’t science and just invent things that we declare to be true, like transfinite infinities, and yeah, as long as we don’t have contradictions, let’s go. The first two frames of the famous XKCD Every Major’s Terrible has fun with this idea:

Sometimes our inventions do give us good models. Cohl Furey explains it in two minutes:
Intrigued? Watch her entire Division Algebras And the Standard Model playlist. Or checkout this article on her work.
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- What are some things that are reasoned about within mathematics? Quantity, structure, change, chance, causality, and space.
- Mathematic reasoning involves finding abstract ________________ and constructing ________________ of real and imaginary phenomena. patterns, models.
- Was math invented or discovered? Probably both.
- What are some of the main branches within mathematics? Foundations, algebra, analysis, discrete, geometry, number theory, topology, applied mathematics.
- What are three theories that claim to be able to formalize “all of mathematics”? Set Theory;
Type Theory;
Category Theory. - What is perhaps the main difference between set theory and type theory? In set theory, everything is a set. In type theory, types come first, and objects are constructed to inhabit the types.
- What are the rules for inhabiting the type of natural numbers? $\dfrac{}{0\!:\textsf{nat}}$$\dfrac{n\!:\textsf{nat}}{sn\!:\textsf{nat}}$
- What does a tuple look like?
$(a, b, c)$- What is $(10, 20, 30)\downarrow 1$?
$20$- What kind of a type do tuples belong to?
A product type.- What is the unit type?
The type with only one inhabitant, $()$.- What is $(2, 8, 3) \bullet (5, 1)$?
$(2, 8, 3, 5, 1)$- Why are sets so effective at formalizing mathematics?
A set expresses the very fundamental notion of an object having a property.- How do sets differ from tuples?
Sets are unordered and do not contain duplicates.- What is the difference between a crisp set and a fuzzy set?
A crisp set is a set where an element is either in the set or not. A fuzzy set is a set where an element can be partially in the set.- How do we denote that $x$ is a member of the set $A$?
$x \in A$- Why isn’t $\{ x \mid x \not\in x \}$ considered a set?
Considering it a set ruins everything because if it were a set, assuming it was a member of itself would imply it was not and assuming it was not a member of itself would imply that it was.- How is set subtraction $A \setminus B$ defined?
$\{x \mid x \in A \wedge x \notin B\}$- What is the difference between $A-B$ and $A \setminus B$?
Nothing, they are the same.- What is the difference between $A \setminus B$ and $A \vartriangle B$?
The first is the set of all elements in $A$ but not in $B$. The second, the symmetric difference, is the set of elements that are in exactly one of $A$ or $B$.- What is $\mathcal{P}(\{a,b,c\})$?
$\{\varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\} \}$- What is $\bigcup \{ \mathbb{Q}, \mathbb{R}, \mathbb{N}\}$?
$\mathbb{R}$- What is $\bigcap \{ \mathbb{Q}, \mathbb{R}, \mathbb{N}\}$?
$\mathbb{N}$- What is $\varnothing \times \varnothing$?
$\varnothing$- What is $\{1,2\}^*$?
$\{(), (1), (2), (1,1), (1,2), (2,1), (2,2), (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), \ldots \}$- What is $\{1, 2\}^0$?
$\{ () \}$- What are the distinct partitions of $\{ a, b \}$?
- $\{ \{a\}, \{b\} \}$
- $\{ \{a,b\} \}$
- What are the distinct partitions of $\{ a, b, c \}$?
- $\{ \{a\}, \{b\}, \{c\} \}$
- $\{ \{a,b\}, \{c\} \}$
- $\{ \{a,c\}, \{b\} \}$
- $\{ \{b,c\}, \{a\} \}$
- $\{ \{a,b,c\} \}$
- Are the set of all even integers and the set of all prime numbers disjoint?
No, they share the number $2$.- Given a relation $R$ defined as a subset of $A \times B$, what are $A$ and $B$ called?
The domain and codomain of $R$.- How do we denote the set of all relations over $A$ and $B$?
$\mathcal{P}(A \times B)$- What is the inverse of the relation $\{(1, 2), (3, 4)\}$?
$\{(2, 1), (4, 3)\}$- Give an example of a relation over $\{a, b, c\}$ that is neither reflexive nor irreflexive.
$\{(a, a), (b, c)\}$ is not reflexive because it does not contain $(b, b)$, and it is not irreflexive because it does contain $(a, a)$.- What is the difference between “asymmetric” and “antisymmetric”?
An asymmetric relation can never have a member of the form $(x,x)$, but an antisymmetric relation can.- What three properties characterize a partial order?
Reflexivity, antisymmetry, transitivity.- Let $R_1 = \{(3,1),(9,8),(2,5)\}$ and $R_2 = \{(8,8),(10,2),(1,7)\}$. What is $R_1 \circ R_2$?
$\{ (10,5) \}$- Let $R = \{ (3, 5), (5, 8), (1, 2), (8, 1) \}$. What are $R^2$ and $R^3$?
$R^2 = \{ (3, 8), (5, 1), (8, 2) \}$
$R^3 = \{ (3, 1), (5, 2) \}$- How do we denote the type of a function from $A$ to $B$?
$A \rightarrow B$- What is another way to show the types on the expression $(\lambda x. x \bmod 2 = 0)\!:(\mathsf{nat \rightarrow bool})$
$\lambda x_{\small \textsf{nat}}. x \bmod 2 = 0$, is sufficient, because we can infer the body has type $\textsf{bool}$.- What is the type of $\lambda x. x$?
$\alpha \rightarrow \alpha$- How do we denote the set of all functions from $A$ to $B$?
$A \rightarrow B$- How do we represent the set $\{ (x, y) \mid x \in \mathbb{N} \wedge y \in \mathbb{N} \wedge x > y \}$ as a function in Type Theory?
$\lambda (x, y)_{\small \mathsf{nat \times nat}}. x > y$- Is $\{ (x, y) \mid x \in \mathbb{Z} \wedge y \in \mathbb{Z} \wedge x = y^2 \}$ considered a function in Set Theory?
No, because both $(1, 1)$ and $(1, -1)$ are in the relation, so that’s two distinct pairs with the same left element.- The set $\mathbb{Z} \times \{ 0 \}$ is a function. Write it in lambda notation.
$\lambda x_{\small \textsf{int}}. 0$- How do you write let $x = 8$ in $2^x - 1$ without the “let”?
$(\lambda x. 2^x - 1)(8)$- How do you write $(\lambda x. x + 3)(5)$ in where-notation?
$x + 3\;\textsf{where}\;x = 5$- The set $\{ (x, y) \mid x \in \mathbb{N} \wedge \textrm{x is even} \wedge y = \frac{x}{2} \} \cup \{ (x, y) \mid x \in \mathbb{N} \wedge \textrm{x is odd} \wedge y = \frac{3x+1}{2} \}$ is a function. Write it in lambda notation, using an if expression.
$\lambda x_{\small \textsf{nat}}. \textsf{if}\;\textit{even}(x)\;\textsf{then}\;\frac{x}{2}\;\textsf{else}\;\frac{3x+1}{2}$- Suppose $f = \lambda x. x^2$ and $g = \lambda x. x + 3$. What are $f \circ g$ and $g \circ f$?
$f \circ g = \lambda x. (x + 3)^2$
$g \circ f = \lambda x. x^2+3$- Suppose $f = \lambda x. 5x + 2$ and $g = f[2/1]$. What are $g(8)$ and $g(1)$?
$g(8) = 42$
$g(1) = 2$- How do you write the function that maps
"x"to 21,"y"to 8,"z"to 55, and every other input to 0, in both lambda notation and as a map?$(\lambda x. 0)[21/\texttt{"x"}][8/\texttt{"y"}][55/\texttt{"z"}]$
$\{ \texttt{"x"}\!: 21, \texttt{"y"}\!: 8, \texttt{"z"}\!: 55 \}$- Let $f = \lambda x. 3x + 5$. What are $f^{-1}$, $f^0$, $f^1$, and $f^2$?
$f^{-1} = \lambda x. \frac{x-5}{3}$
$f^0 = \lambda x. x$
$f^1 = \lambda x. 3x + 5$
$f^2 = \lambda x. 9x + 20$.- What is an injection?
A function that maps distinct inputs to distinct outputs. Also known as a one-to-one function.- What is a surjection?
A function that maps to every element in the codomain. Also known as an onto function.- What is the difference between a function and a partial function?
A function maps every element of the domain to an element of the codomain. A partial function maps every element of the domain to either zero or one element of the codomain.- How do we denote the set of all functions from $A$ to $B$? All partial functions from $A$ to $B$?
$A \rightarrow B$; $A \rightharpoonup B$- If a partial function $f$ has no value at $x$, what do we say $f(x)$ is?
$\bot$- How to we write the partial function mapping the vowels of the English alphabet to their 1-based position in the alphabet in map-notation?
$\{ \texttt{a}\!: 1, \texttt{e}\!: 5, \texttt{i}\!: 9, \texttt{o}\!: 15, \texttt{u}\!: 21 \}$- What kind of number is this: $3 + 8i - 5j + k$?
A quaternion.- What kind of a number is $2 - 5e_0 * 8e_6$?
An octonion.- What do we call $\uparrow$, $\uparrow\uparrow$, and $\uparrow\uparrow\uparrow$?
Exponentiation, tetration, pentation.- How do you conventionally write $5 \uparrow\uparrow 3$?
$5^{5^5}$- Perform “one-step” in the simplification of $8 \uparrow\uparrow\uparrow 5$. That is, write the expression in terms of the $\uparrow\uparrow$ operator alone.
$8 \uparrow\uparrow\uparrow 5 = 8 \uparrow\uparrow (8 \uparrow\uparrow (8 \uparrow\uparrow (8 \uparrow\uparrow 8)))$- What are the ”inverses” of addition, multiplication, and exponentiation?
Subtraction, division, logarithm.- What is $\log_2 1024$ and why?
$10$, because $2^{10} = 1024$- What is $\log_{2} 0.125$ and why?
$-3$, because $2^{-3} = \frac{1}{2^3} = \frac{1}{8} = 0.125$- What is cardinal number?
A number that tells you how many of something there is.- ________________ is more fundamental than counting.
Matching- What are the cardinalities of $\varnothing$, $\{a, b, c\}$, and $\mathbb{Z}$?
0, 3, $\aleph_0$- What is an infinite set?
A set for which there exists a bijection between it and a proper subset of itself.- What is a countable set?
A set for which there exists a bijection between it and $\mathbb{N}$.- Which of the following sets are countable and which are not: $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$, $\mathbb{C}$?
$\mathbb{N}$, $\mathbb{Z}$, and $\mathbb{Q}$ are countable. $\mathbb{R}$ and $\mathbb{C}$ are uncountable.- What does Cantor’s Theorem say?
For any set $A$, $|A| < |\mathcal{P}(A)|$.- Who is the guy that made that freaking amazing set of web pages on big numbers?
Robert P. Munafo- (From the Cohl Furey video) What branches of physics do the complex numbers and the quaternions, respectively, play a central role in?
Quantum mechanics; Special relativity.Summary
We’ve covered:
- What mathematics is concerned with
- Logic notation (just the basics)
- Sets (and relations and functions)
- Numbers
- What else is out there in math world
- Philosophical musings about math and reality
- What does a tuple look like?