Binary Trees
Why Care?
A binary tree is just a $k$-ary tree with $k = 2$. Because $k$ is only 2:
- Binary trees are a bit simpler and easier to understand than trees with a large or unbounded number of children
- There are special traversals besides the usual breadth-first and depth-first traversals
- It is fun (or at least a valuable brain exercise) to generate the formula for the number of distinct binary tree shapes for a given number of nodes
- Binary tree nodes have an elegant linked representation with left and right subtrees
- Binary trees form the basis for efficient representations of sets, dictionaries, and priority queues
These notes present binary trees abstractlyThis page lays out a some basic theory, terminology, and even some mathematics surrounding binary trees. If you need examples first, You could check out the notes on binary search trees and come back to this presentation later.
The material here is still important, as it covers the traversal mechanisms so common on job interviews.
Special Traversals
Like all oriented trees, breadth-first and depth-first traversals exist for binary trees, but there are others:
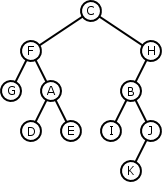
- Preorder: C F G A D E H B I J K
- Inorder: G F D A E C I B K J H
- Postorder: G D E A F I K J B H C
Binary Trees as Strings
In our previous notes on trees awe saw that trees could be represented as strings of the form (root child1 child2 ... childn). But this won’t work for binary trees, since we have to make clear exactly whether a tree with one child has a left child or a right child! So let’s put the root in the middle.
We can make our representation with three simple rules:
- Write the empty tree as:
() - Write a non empty tree as:
(leftSubtree root rightSubtree) - An empty subtree can be, and usually is, omitted.
So for example:
- The tree with one element A is:
(()A()), or just(A) - The tree with A as the root and B as the left child is:
((()B())A()), or just((B)A) - The tree with A as the root and B as the right child is:
(()A(()B())), or just(A(B)) - The tree in the previous section is:
(((G)F(D(A)E))C(((I)B((K)J))H))
How Many Binary Trees Are There?
There are five distinct shapes of binary trees with three nodes:
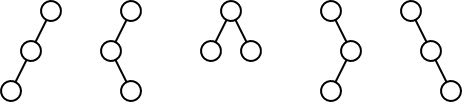
But how many are there for $n$ nodes?
Let $C_n$ be the number of distinct binary trees with $n$ nodes. This is equal to the number of trees that have a root, a left subtree with $j$ nodes, and a right subtree of $(n-1)-i$ nodes, for each $i$. That is:
$C_n = C_0C_{n-1} + C_1C_{n-2} + \cdots + C_{n-1}C_0$
which is:
$C_0 = 1$ and $C_{n+1} = \sum_{i=0}^n C_iC_{n-i}$
The first few terms:
$\begin{array} \\ C_0 = 1 \\ C_1 = C_0C_0 = 1 \\ C_2 = C_0C_1 + C_1C_0 = 2 \\ C_3 = C_0C_2 + C_1C_1 + C_2C_0 = 5 \\ C_4 = C_0C_3 + C_1C_2 + C_2C_1 + C_3C_0 = 14 \end{array}$
You can prove:
$C_n = \frac{1}{n+1}{2n \choose n}$
Here's the number of 8-node binary trees:
$C_8 = \frac{1}{9} \times \frac{16!}{8!8!} = \frac{16 \times 15 \times 14 \times 13 \times 12 \times 11 \times 10}{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} = 13 \times 11 \times 10 = 1430$
Also see Wikipedia's article on the Catalan Numbers.
A Starter Implementation
A binary tree is either empty or is a node with a left subtree and a right subtree.
Since these are the only two choices, let’s go with a sealed interface for our binary tree:
import java.util.function.Consumer;
public sealed interface BinaryTree permits EmptyTree, BinaryTreeNode {
int size();
void preOrder(Consumer<String> consumer);
void inOrder(Consumer<String> consumer);
void postOrder(Consumer<String> consumer);
}
final class EmptyTree implements BinaryTree {
public int size() {
return 0;
}
public void preOrder(Consumer<String> consumer) {
// Nothing to do in an empty tree
}
public void inOrder(Consumer<String> consumer) {
// Nothing to do in an empty tree
}
public void postOrder(Consumer<String> consumer) {
// Nothing to do in an empty tree
}
@Override
public String toString() {
return "()";
}
}
final class BinaryTreeNode implements BinaryTree {
private String data;
private BinaryTree left;
private BinaryTree right;
public int size() {
return left.size() + right.size() + 1;
}
@Override
public String toString() {
return "(" + left + data + right + ")".replace("()", "");
}
public void preOrder(Consumer<String> consumer) {
consumer.accept(data);
left.preOrder(consumer);
right.preOrder(consumer);
}
public void inOrder(Consumer<String> consumer) {
left.inOrder(consumer);
consumer.accept(data);
right.inOrder(consumer);
}
public void postOrder(Consumer<String> consumer) {
left.postOrder(consumer);
right.postOrder(consumer);
consumer.accept(data);
}
}
Here’s an app that uses them:
TODO
As usual, it is good practice to write tests:
TODO
Summary
We’ve covered:
- Why binary trees are interesting
- Preorder, postorder, inorder
- String representations
- Some totally gratuitous math to help exercise your brain
- A basic implementation