Theories in Computer Science
What is a Theory?
We’ll begin with this definition from an actual respected dictionary:
theory (n.)
- A set of statements or principles devised to explain a group of facts or phenomena, especially one that has been repeatedly tested or is widely accepted and can be used to make predictions about natural phenomena.
- The branch of a science or art consisting of its explanatory statements, accepted principles, and methods of analysis.
Sure, sometimes folks use the word “theory” for a hunch or a supposition, but in the arts and sciences, a theory is an organized body of knowledge with explanatory and predictive powers.
Why Study Theory?
We build a theory to organize our knowledge and develop a vocabulary that we can use to reason about things, communicate with others, make predictions, and generate new knowledge.
Without a theory, we can still do things, but not as well: there’s a lot of improvisation, difficulty in communicating ideas, guess work, and flailing around. Your practice will not be as strong, and your insights may be limited. Let’s see how David Bennett expertly makes this point. The key ideas are expressed from 17:21-18:42 (though the whole video is interesting):
Music theory can be helpful in creating music, but can it help us enjoy music more? Certainly! After all, theoretical knowledge adds to our awe of that which we study, allowing us to appreciate the beauty of something at more than just one level:
Theories of Computation
The field we now call Computer Science has a long and fascinating history. Several theories emerged as the discipline took shape. A computer scientist has a working knowledge of these theories and employs them to not only create useful applications and systems, but to advance the state of the art. There are four major theories under the umbrella term “The Theory of Computation.” Two are rather fundamental:
Language Theory
How are computations expressed?
Automata Theory
How are computations carried out?
The third and fourth get into certain specifics but have deep and fascinating philosophical roots:
Computability Theory
What are the fundamental limits of computation?
Complexity Theory
What resources are required to perform certain computations?
To study and apply these theories, we need some context.
Computation augments and amplifies human thought. Modern computers speed up time to such an extent that our reasoning powers are at a qualitatively different level than what we had before these machines. These computational theories help us qualify and quantify how exactly this augmentation occurs. They enable us to ask and answer questions such as
- What even is computation?
- What can and cannot be known through computation?
- What can and cannot even be computed?
- What can and cannot be computed under certain time and space constraints?”
In order to be accepted and useful, these theories must be grounded with practical axioms that match our intuition of what computations actually are. We will take as given that a computer is a finite device and a program is a finite set of instructions.
Language Theory
Language Theory is concerned with how information and computation are expressed. It begins with the question “What is information?” and approaches the question with the hypothesis that any piece of (human-usable) information can be represented as a string of symbols. To see why this hypothesis is useful, note these examples:
91772.3e-8Stay behind the yellow line!ᐊᐃᖓᐃ ᓄᓇᕐᔪᐊᖅ/Pecs/Los Angeles/Berlin/Madrid//1 2/3 0/2 2/2 0/3 2///(* (+ 4 3) (- 9 7))int average(int x, int y) {return (x + y) / 2;}<dog id="30024"><name>Lisichka</name><age>13</age></dog>{"type": "dog", "id": "30024", "name": "Lisichka", "age": 13}∀α β. α⊥β ⇔ (α•β = 0)1. f3 e5 2. g4 ♛h4++
Symbols are chosen from some finite alphabet, such as $\{0,1,2,3,4,5,6,7,8,9\}$ for the language of natural numbers, or $\{0,1,2,3,4,5,6,7,8,9,\textrm{e},\textrm{E},+,-\}$ for the language of floating-point numbers. What is a language? A language (in Formal Language Theory) is a set of strings over an alphabet; that is, some strings are in-the-language and some are not. For example, in the language-of-floating-point-numbers, 3.55E+21 is in the language, but +-9-E...2 is not. Beyond formal language theory, we consider a language to also contain an assignment of “meaning” to each string in the language.
Here’s an obvious, but important, point worth stating: strings in a language represent not only numbers and text and complex data structures, but also abstractions of computations known as functions, which produce output information from input information. Examples:
double, which takes a number and returns twice that numberplus, which takes a pair of numbers and returns their sumnextMove, which takes a game state and returns the next (best?) move that should be madeupperCase, which takes a piece of text and returns a string like it in every way except all letters are in upper casesorted, which takes a list of things and returns a new list containing the same values in sorted ordereven, which takes a number and returns true or false depending on whether the number is eventwice, which takes a function and a value and applies the function to the result of applying the function to the valuejavac, which takes a string in the Java programming language and returns an executable class filejava, which takes a class file and returns (the effect of) its executionpython, which takes a string in the Python programming language and returns (the effect of) its execution
Functions are applied to arguments to produce their results. (The application is sometimes called a invocation or a call.) For example:
double(3.5)$\Longrightarrow$7plus(4, -3)$\Longrightarrow$1upperCase("Please don’t shout!")$\Longrightarrow$"PLEASE DON’T SHOUT!"sorted([4, 7, 1])$\Longrightarrow$[1, 4, 7]even(797)$\Longrightarrow$falsetwice(double, 5)$\Longrightarrow$double(double(5))$\Longrightarrow$double(10)$\Longrightarrow$20python("print(8 * 5 - 2 / 1)")$\Longrightarrow${stdout: "38"}
Functions can be expressed in so many ways. Alonzo Church invented the Lambda Calculus to show that function definition and application could serve as a foundation for mathematics. Here are example functions:
λx. not (equal (mod x 2) 0)λp. λn. λr. λt. times p (power (plus 1 (divide r n)) (times n t))
Abbreviations are okay:
- $\lambda x\,.\,x\:\textrm{mod}\:2 \neq 0$
- $\lambda (p,n,r,t)\,.\,p \times (1 + \frac{r}{n})^{nt}$
There are other notations, too:
(LAMBDA (x) (NOT (EQUAL (MOD x 2) 0)))(Lisp)lambda x: x % 2 != 0(Python)x => x % 2 != 0(JavaScript)(x) -> x % 2 != 0(Java)->(x) {x % 2 != 0}(Ruby)#(not= (mod % 2) 0)(Clojure){$0 % 2 != 0}(Swift)|x| { x % 2 != 0 }(Rust)
In Language Theory, particularly in Programming Language Theory, we study how to express these functions, as well as the data upon which they operate, and the modules, objects, and control structures which house these functions. We study how syntax definitions can be written to define which strings belong to the language, and how semantic definitions can give meaning to these strings. We even study how these languages are used by human beings, something we call pragmatics. But how can we actually compute (or “carry out”, or “evaluate”) these functions? For that we turn to automata theory.
Automata Theory
In Automata Theory, we build and study formal models of computational devices (i.e., computers). Historically, the theory evolved by first examining computing devices through history, then coming up with primitive actions that could capture any kind of computation.
Early Computing Machines
People have designed or built calculating machines for centuries. Notable examples include:
- Abacus
- Antikythera
- Astrolabe
- Pascal’s adder
- Babbage’s Analytical Engine
- Jacquard’s Loom
- and more
“Babbage never foresaw the terrible consequences of his invention—a machine that would autocorrect his name to ‘cabbage’ every single time.” —Philomena Cunk
These were all amazing feats of engineering and human ingenuity in their own right, but Turing was one of the first to capture the essence of computation in a theoretical computing device.
Turing Machines

When Turing was in his early 20s, he set out to prove Hilbert wrong by solving the Entscheidungsproblem in the negative. To do so, he needed to define, formally, what was meant by computation, so he created a simple machine model, or automaton, to capture the essence of computation (or algorithm, or effective procedure). He called machines derived from this model a-machines, but we know them today as Turing Machines. Turing Machines are by no means the only kind of automaton that can carry out computations, but they are special, for a variety of reasons.
Turing set out to formalize what (human) computers did: they followed a set of instructions in which they examined some portion of their paper worksheet, wrote something down or erased something, then moved somewhere else or finished with their result. The actual instructions were based on the human’s state of mind and what was already on the paper. He realized the contents of a two-dimensional sheet of paper could be just as easily represented as a one-dimensional sequence of symbols. So he then reduced the idea to a machine operating on an unbounded sequential paper tape with a read-write head initially pointing to the leftmost symbol of the input. At each step, the machine reads the current symbol, and depending on its current state, possibly rewrites it with a different symbol, moves one square to the left or right, and possibly enters a new state.
Turing’s StoryHistory is important in understanding just about anything. The story of what motivated Turing to work on the foundations of computing and how he arrived at these fascinating machines, and his brilliant insights into the nature of computation are told very well in the book Turing's Vision: The Birth of Computer Science
That book is well worth a read.
Let’s build a Turing Machine to multiply a binary number by four. How would we do this? Well, we just append two zeros to the end of the input! But how can we describe these steps more rigorously? What might the machine’s instructions look like? We might say:
- Begin in the Scanning state, where our job is to look for the end of the input. In this state, we keep moving right until we encounter our first blank, which we replace with a 0 then move right, entering the Doubled state.
- In the Doubled state, we replace the blank with our second zero, entering the Quadrupled state.
Here is how our machine operates with the number five (binary 0101) initially on the tape (And oh, following convention, we use # for blank squares, just because it is easier to see!):
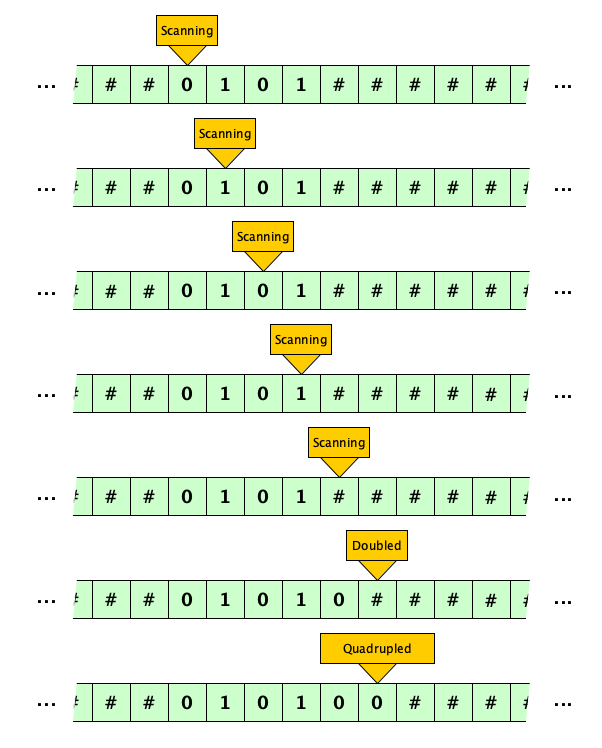
Nice! 5 × 4 is indeed 20 (binary 010100). Now let’s capture the the multiply-by-four machine in all its glorious generality:
| When in state | Looking at | Perform these actions | And go to state |
|---|---|---|---|
| Scanning | 0 | Move right | Scanning |
| Scanning | 1 | Move right | Scanning |
| Scanning | # | Print 0, Move right | Doubled |
| Doubled | # | Print 0 | Quadrupled |
This says: starting in the Scanning state, while you see a 0 or 1, just move right, but if you see a blank, replace with a 0, move right, and go to the Doubled state. In this state, if you see a blank, replace with a 0 and go to the Quadrupled state. There is no place to go from here, so we’re done.
We can give a pictorial representation of the TM program as a state diagram:
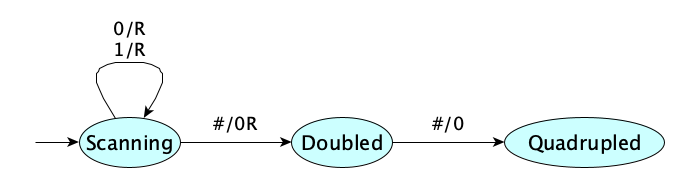
Turing’s original design allowed any number of actions, but folks realized that you could make each action be a print and a move only. Print-less moves in the original machine could be handled by just printing the input symbol. So our multiply-by-four machine could have this table:
| When in state | Looking at | Move | And go to state | |
|---|---|---|---|---|
| Scanning | 0 | 0 | Right | Scanning |
| Scanning | 1 | 1 | Right | Scanning |
| Scanning | # | 0 | Right | Doubled |
| Doubled | # | 0 | Right | Quadrupled |
(Ok, yeah, wait, having to do that last move is annoying perhaps but it does not hurt.)
This “standardized form” leads to the more conventional state diagram:

And, if you like, you can even change up the table a bit! See if you can make sense out of this:
| 0 | 1 | # | |
|---|---|---|---|
| S | 0RS | 1RS | 0RD |
| D | — | — | 0RQ |
| Q | — | — | — |
We will generate Turing Machines to (a) floor-divide by four, (b) increment a binary number by 1, (c) compute the two’s complement of a binary number, and (d) compute the value of a binary number modulo 2.
Turing Machines are not the only kind of machine that we can use as a model of computation, but they have become the most popular. When we study automata theory and Turing Machines more formally, we’ll encounter some really cool ideas:
- Turing Machines that output boolean results are essentially language recognizers, so there is this fascinating connection between language theory and automata theory.
- Turing Machines can be encoded as strings and processed by other Turing Machines.
- There exists one particular Turing Machine, called the Universal Turing Machine $U$, that, when run starting with the encoding of a machine $M$ and a string $w$ on its tape, will compute exactly what $M$ would compute with input $w$!
- Researchers have used Turing Machines as the basis for studying computability and complexity theory.
We‘ll cover Turing Machines later in the course, but for the impatient, here’s a video (note that Jade uses the standard form labels in her state diagrams):
Other Kinds of Automata
Turing Machines are not the only model of what we think of as computation (though they might be the most famous). Other models that have been created include:
- Register Machines
- The Lambda Calculus
- Post Systems
- Partial Recursive Functions
- Analytic Grammars
- Queue Automata
- Stack Automata
- String Rewriting Systems
- Cellular Automata
Some have equivalent “computability and recognition power” as Turing Machines, while others do not. But none have greater computing power! What do we mean by “computability and recognition power”? That’s the domain of our next theory, computability theory.
Computability Theory
Now for our next philosophical question. Can every function be represented as a string of symbols that we can process with a machine? In other words, is there a program for every function?
It turns out that the answer to this is no.
Here’s why. Programs are just strings, so we can list them in increasing alphabetic order. Programs can be thought of as representing functions in $\mathbb{N} \rightarrow \mathbb{N}$ (since all data can be encoded in binary). Call the enumeration $f_0, f_1, f_2, \ldots$. But $\lambda n. f_n(n)+1$ isn’t in the list! Bottom line:
There exist functions that cannot be computed by a computing machine.
Hey, this is philosophically interesting.
That explanation of why uncomputable functions exist was given rather nonchalantly. Did it make sense? It might not have right away because it is an instance of a very powerful proof technique called diagonalization which was at first somewhat controversial. Carry out this proof by sketching the hypothetical list of all functions as a matrix: each row is a function and each column is the argument, and each cell is the result of applying the function (row) to the argument (column). Look at how $\lambda n. f_n(n)+1$ is generated. Do you see why the technique is called diagonalization? Do you see why it works? 🤯
So which functions can be computed? People have, over the years, created many models of computation—the Lambda Calculus, Post Production Systems, Phrase Structure Grammars, Partial Recursive Functions, Random Access Machines, and more. But get this: all have turned out to be equal in power, in terms of what they can compute, to the Turing machine! Even enhancing the basic Turing Machine design with non-determinism or even multiple tapes won’t increase its computing power. These facts suggest the class of computable functions is fundamental. The Church-Turing Thesis claims that what we intuitively understand as the “computable functions” are precisely those for which a Turing Machine can be given, i.e.,
A function $f$ is computable if and only if a there exists a Turing Machine that outputs $f(x)$ for any input $x$.
Remember that Universal Turing Machine briefly mentioned above? It is “universal” because it can simulate any Turing Machine. If the Church-Turing Thesis is true, it’s really universal: it can compute any computable function.
Computability Theory is concerned with figuring out which functions are and are not computable.
Turing Complete
Because Turing Machines capture that which is computable, any computational model that can simulate a Turing Machine is called Turing Complete. Being Turing-Complete is a badge of honor, as it means your model can compute anything that is computable.
Read more at Wikipedia.
How about an example? We’ll use JavaScript rather than TMs to simplify the explanation. Let’s write a function called halts that will determine if a function halts on a given input. So we would like:
halts(Math.sqrt, 100) ⟶ true
halts(x => {while (x) {}}, true) ⟶ false
The idea is simple. Just analyze the input and see if it will halt. But it turns out to be logically impossible to write this function. Why? Assume you can write it. Then consider:
function fox(f) {
if halts(f, f) while (true) {}
}

Now consider the expression halts(fox, fox). Woah. We have an antinomy. The assumption you could write halts leads to a contradiction, so you can not write this function to work for all inputs. Interestingly, you can write:
function halts(f, x) {
f(x);
return true;
}

So if f(x) halts, you’ll eventually know it, but if it doesn’t, we may never know.
Complexity Theory
Computability theory gives us theoretical limits on what can and cannot be computed, but doesn’t tell us what is practically computable. (A problem requiring 2100 years to complete is not worth running.) The question “What resources are required to perform certain computations?” or in other words “How much time and memory is needed to solve this problem?” give rise to Complexity Theory.
Complexity Theory gives us results such as “This function requires ________________ to compute”:
- only a single step
- only a fixed number of steps
- logarithmic time
- linear time
- quadratic time
- polynomial time
- exponential time
- no more than a single cell of scratch memory
- scratch memory in the form of a stack (which is very efficient)
- logarithmic space
- linear space
- polynomial space
- exponential space
It gets (massively) more interesting, because the theory deals with time and space performance on non-deterministic machines, and parallel machines, and interactive machines, and quantum computers, too. It even considers probabilistic algorithms. Interested? Check out the amazing Complexity Zoo.
Complexity Theory has philosophical as well as practical use. Make sure you are familiar with one of the most famous open questions in all of complexity theory, and perhaps even all of computer science, namely: Does $P = NP$? (Solve it and you will win a million dollars!)
Oh, wait! Here’s Jade again with another great explainer:
There is so, so, much information out there about the P vs. NP question as it really seems to captivate the public. Not unlike Gödel’s Incompleteness Theorems.
I, Scott Aaronson, hereby formally disown my statement about how “everyone who could appreciate a symphony would be Mozart” if P=NP.
In 2014, he wrote a new post on the scientific case for P≠NP. Read the later post. What do you think?Working With These Theories
We’ve only briefly introduced the major concerns of four computer science theories without any real depth (or breadth). We’ll have a chance to see each theory in more detail later, covering aspects such as:
- Formal, mathematical, definitions of languages (via grammars) and automata
- Restricted grammars and automata that capture specific kinds of computation
- Language hierarchies capturing both computability and complexity concerns
- Models of computation other than the Turing Machine
- More examples of non-computable functions (beyond the “Halting Problem” we saw above)
- How to construct a Universal Turing Machine
- Examples of languages in many of the common complexity classes
- How to determine the complexity of a problem
- How to create grammars for realistic programming languages
- Why non-trivial programming languages require both a static and dynamic semantics
- Extending these ideas into the much larger Programming Language Theory (PLT)
- How to run a program given its source code (interpret)
- How to translate one programming language into another (compile)
Theories and Creativity, Again
In much the same way that Bennett pointed out that music theory can expand your abilities in music composition, and Feynman spoke of theoretical knowledge in science only expanding and enhancing the feelings of awe and beauty when contemplating nature, might computer science theory enhance one’s imagination for creating new worlds that Booch talks about here?

Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- What exactly is a theory, in the context of art and science? An organized body of knowledge with explanatory and predictive powers.
- Why are theories important? They provide us with a vocabulary to communicate ideas, test hypotheses, and generate new knowledge.
- What are the four major computation theories and what are they concerned with?
- Language Theory: expressing computations
- Automata Theory: carrying out computations
- Computability Theory: What can and cannot be computed?
- Complexity Theory: Resources required for certain computations
- What is a language, in formal language theory? A set of strings over some finite alphabet.
- What is the lambda calculus seemingly most concerned with representing and manipulating? Functions
- Who came up with the idea of formalizing computing via the Lambda Calculus? Alonzo Church
- Who came up with the idea of formalizing computing via the Turing Machine? Alan Turing
- What was Turing trying to do when he realized he would have to do no less than formally define the very notion of an algorithm (or computational process)? He was trying to show Hilbert’s Entscheidungsproblem did not have a solution
- On what did Turing more-or-less base his fundamental idea of how a formal (abstract mechanical) computing device should work? (Human) computers, calculating on paper by moving through mental states looking at symbols, adding new symbols, and erasing existing ones.
- What are the main components of a Turing Machine?
- A control unit made up of states and a transition relation, and
- An infinite one-dimensional tape with cells that can each hold a single symbol or be blank.
- Why is Turing’s discovery/invention of the Universal Turing Machine so profound? It means that truly general-purpose, programmable computing machines exist (i.e., we don’t need specialized machines for all computations).
- How can we prove there are functions that cannot be computed? By diagonalizing over an assumed enumeration of all functions.
- What does the Church-Turing Thesis say? That the Turing Machine lines up exactly with our notion of what is intuitively computable.
- What are the language classes P and NP? P is the set of languages decidable in polynomial time on a deterministic TM; NP is the set of languages decidable in polynomial time on a nondeterministic TM.
- Does P = NP?
- Did Scott Aaronson really write “everyone who could appreciate a symphony would be Mozart”? How does he feel about writing that these days? He did indeed write that but he regrets writing it now.
- What are some variations we can make to Turing Machines that possibly affect complexity (if not computability)? Randomized machines, probabilistic machines, quantum machines.
- How does Grady Booch distinguish the work in material domains (physics, chemistry, biology, etc.) from that of computer science? Scientists in material domains observe the cosmos and reduce it to simple principles; computer scientists start with simple principles and from them create new worlds bound only by the imagination.
Summary
We’ve covered:
- What a theory is
- Why study theory?
- Theories within computer science
- What Language Theory is
- What Automata Theory is
- What Computability Theory is
- What Complexity Theory is
- Where we can go from here