Syntax

Motivation

A language gives us a way structure our thoughts. Utterances in a language (called programs in a programming language) have a kind of internal structure, for example:

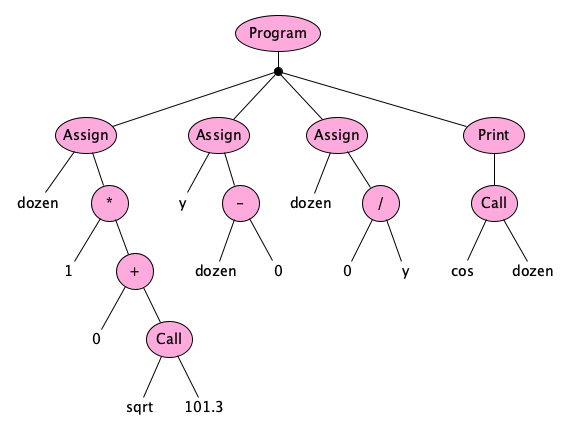
We generally capture this structure as a sequence of symbols; for example, the structure above might appear as:

dozen = 1 * (0 + sqrt(101.3));
y = dozen - 0;   // TADA 🥑
dozen = 0 / y;
print cos(dozen);//

or even:

MOVE PRODUCT OF 1 AND (SUM OF 0 AND SQRT OF 101.3) INTO DOZEN.
MOVE DIFFERENCE OF DOZEN AND 0 INTO Y.
COMMENT TADA 🥑
MOVE QUOTIENT OF 0 AND Y INTO DOZEN.
PRINT COSINE OF DOZEN.
COMMENT

or even:

(program 
  (assign dozen (* 1 (+ 0 (call sqrt 101.3))))
  (assign y (- dozen 0))            ; TADA 🥑
  (assign dozen (/ 0 y))
  (print (call cos dozen))          ;

Of course, we don’t have to use strings! Visual languages do exist:

Text vs. Pictures

Text is more dense than pictures, and more directly machine readable at times (no computer vision machine learning necessary). Even if your language was expressed with pictures, there will be an underlying byte-array, or string, representation for storage and transmission.

So our focus from now on will be on text.

If you were a language designer, you’d deal with questions such as:

• Is code expressed in terms of blocks? Visual graphs? Text?
• If text, which characters are allowed? Is whitespace significant? Is case significant?
• Is there a lot of punctuation? Symbols? Or is it mostly words? If words, what natural language are you biased toward?
• How do we do comments? Pragmas? Directives?
• Do we express structure with indentation, curly-braces, terminating-end, or nested parentheses?
• Should operations have a functional (length(a)) or message-oriented (a.length) feel?
• What kind of shorthands and idioms should be made available?
• How do program units map to files or other physical containers?

Definition

The syntax of a programming language is the set of rules that define which arrangements of symbols comprise structurally legal programs—and for each structurally legal program, what its structure actually is.

Syntactic rules should be able to tell us that these sentences are not well-formed in English:

• telescope a they the With hit saw.
• yqvfe.,--)AO7%;;;;;;;; ; !dogs

but that these are:

• They hit the telescope with a saw.
• They saw the hit with a telescope.

and so is this famous one, due to Chomsky:

• Colorless green ideas sleep furiously.

Learning by Doing

Let’s learn about syntax by going through the process of designing a syntax for a small language.

We’ll assume the preliminary phases of language design—identifying the purpose (education), scope (simple arithmetic computation), audience (students), and name (Astro) of our language—have been done, and now it is time for the technical work to begin.

We first sketch a program to illustrate the syntactic features we want:

// A simple program in Astro

radius = 55.2 * (-cos(2.8E-20) + 89) % 21;    // assignment statement
the_area = π * radius ** 2;                   // a built-in identifier
print hypot(2.28, 3 - radius) / the_area;     // print statement

Next, we put our ideas into words. A first pass: “Programs are structured as a sequence of one or more statements, each of which is an assignment or print statement, with expressions formed with numbers, variables, function calls, and the usual arithmetic operators, which can have parentheses when needed. Comments look like the slash-slash comments of C-like languages.”

Natural language isn’t super precise, so as we sometimes do in design, we’ll next turn thoughts into pictures.

A program is a sequence of one or more statements:

There will be two kinds of statements: assignments and print statements:

Assignments and print statements look like this:

An identifier is the computer science word for a name you attach to an entity (a variable, constant, function, type, parameter, or similar thing). A keyword is a special word in your language, like let or if or while—these words generally do not name things—they are just used to structure the code. If a keyword is not allowed to be an identifier, we call it a reserved word. Astro has one reserved word: print.

Identifiers in Astro begin with a letter, and can have letters, digits, and underscores (examples: x, last_attempt, p1, p2, overTheLimit, bot8675309_jEnNy). We will call letters, digits, and underscores identifier characters (idchars). But notice that print is not allowed to be an identifier:

How is the reserved word print specified? We have to be careful. It’s not just the five letters p, r, i, n, and t. If it were then the program:

    printy;

would be legal! It would be the five characters spelling print followed by a legal expression, namely the identifer $y$. We want the word print to not bleed into any following characters that might be part of an expression. In other words, print must not be immediately followed by an identifier character:

A statement performs an action (perhaps with a side effect), but expressions represent the computation of a value. Expressions can be numbers, identifiers (representing variables), function calls, or can be made up of operators applied to other expressions. We can put parentheses around any expression. This will do the trick (but spoiler alert: we will have to change it later):

We mentioned numerals here, so let’s define these. We’ll keep things in decimal only (no worries about hex or binary), and use the times-ten-to-the notation from popular programming languages:

What about letters and digits? Well digits are pretty easy:

For letters, well, there are tens of thousands of these in Unicode, so we’ll just say the rule for letter is “built-in.”

Lexical and Phrase Syntax

Did you notice that we used two kinds of nodes in our syntax diagrams? We used ovals for constructs that internally cannot have spaces in them; we call these lexical nodes, or tokens. We used rectangles for constructs whose components can have spaces between them; we call these phrase nodes, or phrases. The special category called space defines what can separate tokens within phrases.

In the little language Astro that we are designing, the separators are the space character, the tab character, the carriage return character, the linefeed character (the linefeed (U+000A) is pretty much universally accepted as the “newline”), and comments. Comments function as spaces, too! For comments, we chose to start with // and go to the end of the current line.

We also followed an accepted convention to start the names of lexical nodes with lowercase letters and capitalize the names of phrase nodes.

Another convention we will follow for programming language syntax is to take the following as predefined:

• letter, for any Unicode letter
• digit, for "0".."9"
• alnum, for letter | digit
• upper, for any Unicode uppercase letter
• lower, for any Unicode lowercase letter
• hexDigit, for digit | "a".."f" | "A".."F"
• any, for any Unicode character at all

and also allow these conveniences:

• \u{ and }, delimit a code point in hex and stands for the unicode character with that code point
• \n, for the LF character (same as \u{a})
• \r, for the CR character (same as \u{d})
• \t, for the tab character (same as \u{9})
• \", for the quote character (same as \u{22})
• \', for the apostrophe character (same as \u{27})
• \\, for the backslash character itself (same as \u{5c})

Note that any can be defined as \u{0}..\u{10ffff}.

Remember

The term space, though it looks like a lexical node, is something meta; it is treated specially.

Let’s spend some more time on the philosophical significance of the separation of lexical and phrase syntax.

The lexical syntax, with the exception of the special rule for space, show us how to combine characters into words and punctuation which we’ll call tokens. The phrase syntax show us how to combine words and symbols into phrases (where the words and symbols can, if you wish, be surrounded by spacing).

Now if we wanted to recognize whether a string is “in” a language, we can figure this out in two phases. The first phases uses the lexical rules to tokenize a stream of characters into a stream of tokens, and the second phase uses the phrase rules to parse the token stream into the parse tree. Here’s an example. The source string:

  print( // ⿇🌿
420 );

is made up of these characters:

SPACE SPACE LATIN SMALL LETTER P LATIN SMALL LETTER R LATIN SMALL LETTER I LATIN SMALL LETTER N LATIN SMALL LETTER T LEFT PARENTHESIS TAB SOLIDUS SOLIDUS SPACE KANGXI RADICAL HEMP HERB LINEFEED DIGIT FOUR DIGIT TWO DIGIT ZERO SPACE RIGHT PARENTHESIS SEMICOLON

When we follow the lexical rules to this character stream, skipping the spaces (and comments), we get the token stream:

print ( num(420) ) ;

Next, we follow the phrase rules allows us to uncover the parse tree:

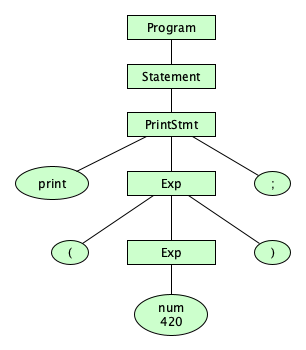
A very important thing to note: The frontier of the parse tree is the token stream.

The parse tree ends at tokens, not characters

Please take the time to consider how silly it would be if the parse tree expanded all of the lexical rules down to characters. Having the parse tree stop at tokens is a good example of what we would call “breaking a complex problem down into simpler parts.”

Dealing With Ambiguity

How are we doing so far? We are able to distinguish well-structured Astro programs from all other Unicode strings. But there are some things we haven’t dealt with yet. For one, we have some strings with multiple structural forms. For example, the phrase 9-3*7 can be parsed in two ways:

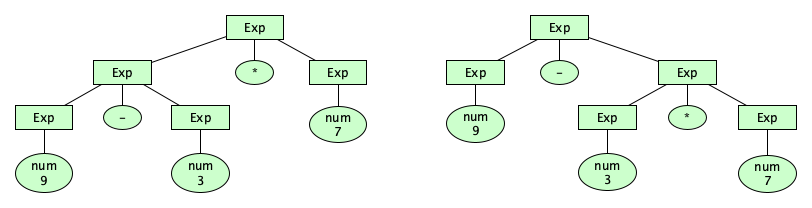
Having more than one parse tree for a given input string means that our syntax description is ambiguous. It’s possible to handle this particular kind of ambiguity in the syntax. Here’s how.

Precedence

We can create rules that force certain operators to be applied before others; that is, the precedence of operators can be enforced in our syntax definition. To do so, we define additional syntactic categories. We say:

• An expression is a sequence of one or more terms, separated by additive operators.
• A term is a sequence of one or more factors, separated by multiplicative operators.
• A factor is made up of primaries, separated by exponentiation operators, or a factor can just be a negated primary.
• A primary is the most basic expression possible: either a simple identfier, a numeral, a call, or a parenthesized expression. Parentheses allow unlimited nesting.

We can write:

Great! Now there is one and only one parse tree for that previously problematic expression:

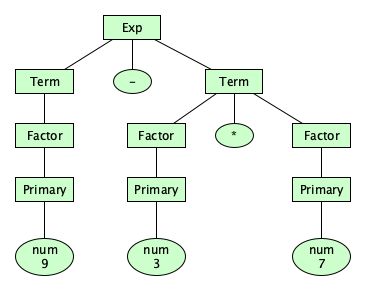
Note that the new syntax has forced the binary operators into a precedence hierarchy!

• + and - have the lowest precedence.
• *, /, and / have the next higher precedence.
• ** has the highest precedence.

Of course, you can think of parenthesized expressions as being done before anything else, though we don’t usually think of these as operators.

Associativity

Wait, we are not done with structuring our operators just yet. The way things stand now, the parse tree for 3-8-5 looks pretty flat:

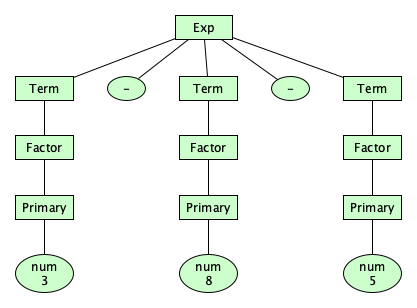
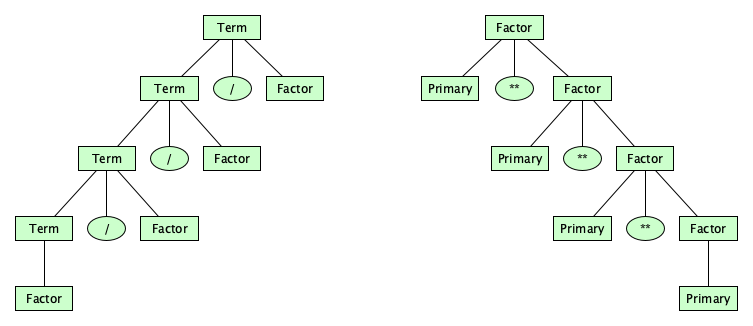
It doesn’t suggest whether we mean to compute (3-8)-5 (which would be -10) or 3-(8-5) (which would be 0). We can give a syntax that makes this clear. In our design, let’s make the additive and multiplicative operators left-associative and the exponentiation operator right-associative:

How the heck does this work? Study these parse trees, and hopefully the insight will come to you! (Hint: remember the syntax is designed to force the tree to “come out” a certain way.

Grammars for Programming Languages

Syntax Diagrams are fine for giving an overview of program structure, but, like all pictorial notations, they can take up a lot of space and are rather hard to process by a machine. If we could write a denser, text-based description of a syntax, we could write a program that checked a candidate program for conformance with the syntax! This is exactly what compilers, interpreters, and related tools do.

Let’s translate the syntax diagrams above into a grammar for Astro. We will use an analytic grammar, rather than a generative one, as we want to take advantage of negative lookahead to help describe our keywords and identifiers.

The Problem of Context

Question: Does the grammar we have defined above for Astro capture the following (desirable) rule:

“You can only use an identifier if it has been previously assigned to.”

Answer: It does not.

Enforcing this rule requires knowledge of context. That is, the syntactic rule for producing expressions such as calls and arithmetic operations would need to somehow know which identifiers appeared on the left hand side of some previous assignment statement. This turns out to be so hard that even designers of real programming languages omit enforcement of contextual rules from the grammar! In fact, while the official grammar for Java will not derive this program:

class A {2 / == {{;

and report a syntax error, a Java compiler will say that this program:

class A {int x = y;}

is structurally well formed according to the official syntax of the Java language! The compilation unit consists of a type declaration that is a class declaration whose body consists of a field declaration with a type, a name, and an initializing expression which is an identifier. But we know this program is not legal, since the identifier y has not been declared. It’s not only Java that has grammars overspecifying things: this C program has multiple problems despite being well-formed according to the C grammar:

/*
 * This program is derivable by the official grammar for C.
 */
int main() {
    f(x)->p = sqrt(3.3);
    return "dog";
}

This is because it’s really really really really really really really really hard and really really really really really really really really ugly to define contextual rules grammatically! Capturing an “all identifiers must be declared before use” constraint would require that a grammar rule for expressions not just generate any identifier, but only certain identifiers known from some outside context. Context! In general, capturing context in a grammar leads to grammars that:

• are incredibly difficult for humans to figure out,
• are nearly impossible for humans to read (they’re ridiculously long and incredibly weird),
• look nothing at all like the way we would check these rules in a compiler,
• give rise to trees that are weird since expansion of nodes is based on sibling nodes, not just the parent, which makes semantics hard to define, and
• horribly expensive even for a computer to parse.

Try the following exercise if you’re not convinced:

Sometimes there are constraints that we can (theoretically) capture in a context-free syntax, but that we might not want to. Try the following two exercises:

Defining Contextual Constraints

So many programming language rules require context. Here’s a small sampling from various languages:

• Identifiers must not be redeclared within a scope
• Identifiers may not be used in a place where they might not have been initialized
• Types of all subexpressions must be consistent in an expression
• The correct number of arguments must appear in a call
• Access modifiers (private, protected, public) must be honored
• All execution paths through a function must end in a return
• All possible arms of a match or switch or discriminated union must be covered
• All abstract methods must be implemented or declared abstract
• All declared local variables must be used
• All private methods in a class must be used
• ...and so many more

For our running example language, Astro, our constraints are:

1. The following identifiers are built-in:
   • π, a number
   • sqrt, a function of exactly one argument
   • sin, a function of exactly one argument
   • cos, a function of exactly one argument
   • hypot, a function of exactly two arguments
2. An identifier cannot be used in an expression unless it is one of the built-in identifiers or has been previously assigned to.
3. All function calls must accept the proper number of arguments.
4. The built-in identifiers cannot be assigned to.
5. Identifiers declared as functions can only be called, not used in any other context. Identifiers declared as numbers cannot be called.

That’s informal prose. Can we capture the rules in a formal notations? Well, context sensitive grammars are too hard to write, too hard to understand, and too hard to parse, so we need other options. There are at least two:

• Use a completely new kind of grammatical formalism. Some of these do exist, including Attribute Grammars and Two-Level Grammars.
• Push contextual constraints into the world of semantics. Let the syntax be happy with undeclared identifiers appearing in expressions (as long as the expressions are otherwise well formed). With this approach, we say that using undeclared identifiers is ”meaningless,” you know, a semantic problem. And because the meaning (ahem, semantics) is computed before the program is run, we would call constraint violations static semantic errors.

Which take do you prefer? Slonneger and Kurtz take the former approach, writing:

The classification of such an error entails some controversy. Language implementers, such as compiler writers, say that such an infraction belongs to the static semantics of a language since it involves the meaning of symbols and can be determined statically, which means solely derived from the text of the program. We argue that static errors belong to the syntax, not the semantics, of a language. Consider a program in which we declare a constant:

    const c = 5;

In the context of this declaration, the following assignment commands are erroneous for essentially the same reason: It makes no sense to assign an expression value to a constant.

    5 := 66;
    c := 66;

The error in the first command can be determined based on the context-free grammar (BNF) of the language, but the second is normally recognized as part of checking the context constraints. Our view is that both errors involve the incorrect formation of symbols in a command—that is, the syntax of the language. The basis of these syntactic restrictions is to avoid commands that are meaningless given the usual model of the language.

Though it may be difficult to draw the line accurately between syntax and semantics, we hold that issues normally dealt with from the static text should be called syntax, and those that involve a program’s behavior during execution be called semantics. Therefore we consider syntax to have two components: the context-free syntax defined by a BNF specification and the context-sensitive syntax consisting of context conditions or constraints that legal programs must obey.

Indentation-Sensitive Syntax

In addition to the context issues that exist between a language’s syntax and its static semantics, similar issues exist between the lexical syntax and phrase syntax in languages that are indentation-sensitive. Traditionally, lexical analysis proceeds as if the size of whitespace runs don’t matter very much. But in languages like Python and Haskell, they do. A lot. We cannot just skip any whitespace between tokens the way we’ve done so above!

The way to handle indentation sensitivity is, during lexical analysis, keep track of indentation levels (in some sort of context object), and replace certain runs of whitespace with INDENT and DEDENT tokens.

The process isn’t too hard. For complete details, read the section on indentation in the Lexical Analysis chapter of the Python Language Reference.

Abstract Syntax

Parsing is a lot of work. Specifying programs as strings of characters requires extra tokens (parentheses) and extra categories (Term, Factor, and Primary) in order to capture precedence, and crazy rule writing to get associativity correct. We have semicolons to terminate statements. Real languages have lots and lots of punctuation as well. Parse trees can get huge!

Dealing with spaces, comments, tokens, punctuation, precedence, and associativity is important in the early stages of language processing (the thing that interpreters, compilers, syntax highlighters, debuggers, and performance monitoring systems do). But once source code is parsed and the internal structure is uncovered, we can simplify the parse tree into something much simpler for the later stages of language processing (e.g., semantic analysis, optimization, translation, code generation, or execution). These later stages don’t really need that much from a parse tree. We can abstract away a lot of the messy stuff, and translate our parse tree into an abstract syntax tree:

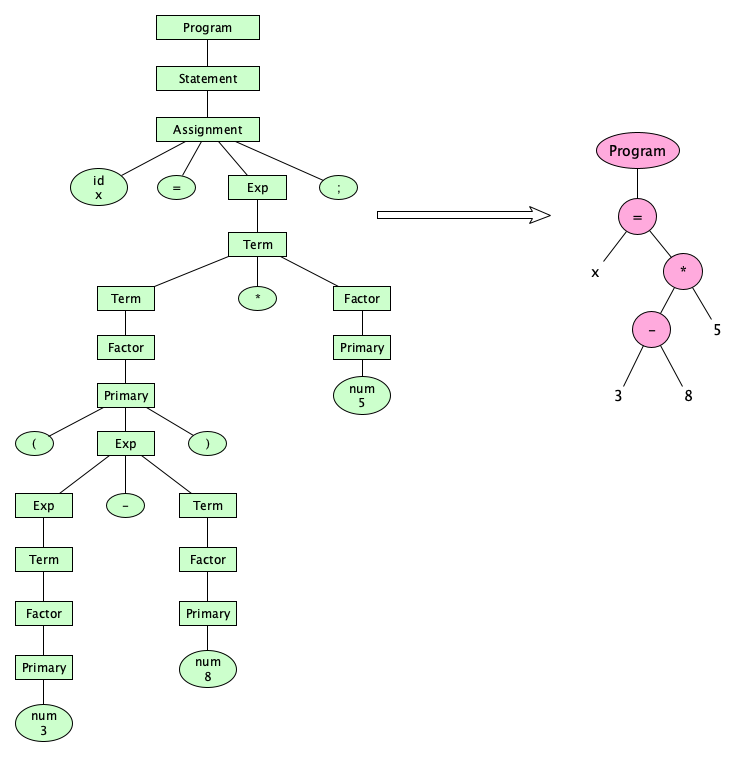
So much simpler! And by the way, since these simpler trees have become known as abstract syntax trees (ASTs), it turns out that, yes, parse trees have become known as concrete syntax trees (CSTs).

How do we come up with an abstract syntax? Focus on what a program is trying to express, without worrying about punctuation. You don’t even have to worry about precedence and associativity (or even parentheses) because that stuff was already “taken care of” earlier. So cool! Here’s how we think about it for Astro:

• A program is a sequence of statements
• A statement is either an assignment or a call
• An assignment is an identifier being assigned an expression
• A call has an identifier for the function name and a list of expressions for its arguments
• An expression can be a number, identifier, a unary operator applied to an operand, two expressions with a binary operator, or a call.

If you want to formalize this, you can write a tree grammar:

$ \begin{array}{llcl} n: & \mathsf{Nml} & & \\ i: & \mathsf{Ide} & & \\ e: & \mathsf{Exp} & = & n \mid i \mid -e \mid e+e \mid e-e \mid e\,\texttt{*}\,e \mid e\,/\,e \mid e\,\texttt{\%}\,e \mid e\,\texttt{**}\,e \mid i\;e^*\\ s: & \mathsf{Stm} & = & i = e \mid \texttt{print}\;e\\ p: & \mathsf{Pro} & = & \texttt{program}\;s^+\\ \end{array}$

Some people like to write tree grammars another way:

$\mathsf{Program} \rightarrow \mathsf{Stmt}+$
$\mathsf{Assign: Stmt} \rightarrow \mathsf{id}\;\mathsf{Exp}$
$\mathsf{Print: Stmt} \rightarrow \mathsf{Exp}$
$\mathsf{num: Exp}$
$\mathsf{id: Exp}$
$\mathsf{Negate: Exp} \rightarrow \mathsf{Exp}$
$\mathsf{Plus: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Minus: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Times: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Divide: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Remainder: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Power: Exp} \rightarrow \mathsf{Exp}\;\mathsf{Exp}$
$\mathsf{Call: Exp} \rightarrow \mathsf{id}\;\mathsf{Exp}*$

When translating to an abstract syntax, we not only get rid of intermediate syntax categories, but we also drop parentheses, commas, semicolons, brackets, and pretty much all punctuation. Some of the smaller keywords that you see in larger programming languages (in, to, of) also are not needed. Punctuation really only exists to give a “tree structure” to our linear program text. Once we have uncovered the tree structure in the CST, we just carry it over naturally to the AST.

Don’t break down the tokens either

When writing an abstract syntax, you can assume that the tokens (the lexical syntax) is already done for you.All lexical categories (like identifiers and numeric literals in our example above) are primitive.

Multiple Concrete Syntax Trees

So ASTs allow us to focus on programming language capabilities without worrying about syntactic details that people can reasonably have different preferences about. Take a look at this AST (in some hypothetical language, not Astro):

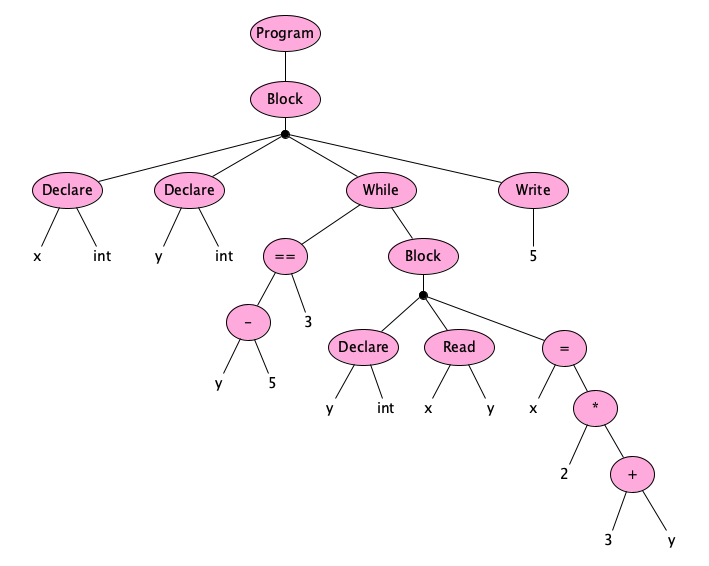
Stop! Don’t scroll by! Study this tree! What is this program “saying”?

It appears to be a program in a language whose tree grammar probably looks like this:

$ \begin{array}{llcl} n: & \mathsf{Nml} & & \\ i: & \mathsf{Ide} & & \\ t: & \mathsf{Type} & = & \mathtt{int} \mid \mathtt{bool} \\ e: & \mathsf{Exp} & = & n \mid i \mid -e \mid e+e \mid e-e \mid e\,\mathtt{*}\,e \mid e\,/\,e \mid e\,\mathtt{**}\,e \\ & & & \mid\; e < e \mid e \leq e \mid e\mathtt\,{==}\,e \mid e \neq e \mid e > e \mid e \geq e \mid i\;e^*\\ s: & \mathsf{Stmt} & = & i = e \mid \mathtt{read}\;i^+ \mid \mathtt{write}\;e^+ \mid \mathtt{while}\;e\;b \\ d: & \mathsf{Dec} & = & \mathtt{declare}\;i\;t\\ b: & \mathsf{Block} & = & d^* \;s^+\\ p: & \mathsf{Pro} & = & \mathtt{program}\;b\\ \end{array}$

But what does the actual concrete syntax look like? There’s no specific answer. There are an infinite number of possibilities! Here is just a small sampling of programs that could have generated that AST:

program:
    var x, y: int
    // In this language, indentation defines blocks
    while y - 5 == 3:
        var y: int
        get(x)
        get(y)
        x = 2 * (3 + y)
    put(5)

int x, y;
while y - 5 = 3 {
    int y;
    STDIN -> x;
    STDIN -> y;
    x <- 2 * (3 + y);
}
STDOUT <- 5;

COMMENT THIS LOOKS LIKE OLD CODE
DECLARE INT X.
DECLARE INT Y.
WHILE DIFFERENCE OF Y AND 5 IS 3 LOOP:
    DECLARE INT Y.
    READ FROM STDIN INTO X.
    READ FROM STDIN INTO Y.
    MOVE PRODUCT OF 2 AND (SUM OF 3 AND Y) INTO X.
END LOOP.
WRITE 5 TO STDOUT.

(program
  (declare x int)
  (declare y int)
  (while (= (- y 5) 3)
    (define (y int))
    (read x y)
    (assign x (* 2 (+ 3 y)))
  )
  (write 5)
)

<program>
  <declare var="x" type="int"/>
  <declare var="y" type="int"/>
  <while>
    <equals>
      <minus><varexp ref="y"/><intlit value="5"/></minus>
      <intlit value="3"/>
    </equals>
    <declare var="y" type="int"/>
    <read vars="x y"/>
    <assign varexp="x">
      <times>
        <intlit value="2"/>
        <plus>
          <intlit value="3"/>
          <varexp ref="y"/>
        </plus>
      </times>
    </assign>
  </while>
  <write>
    <intlit value="5"/>
  </write>
</program>

More AST Examples

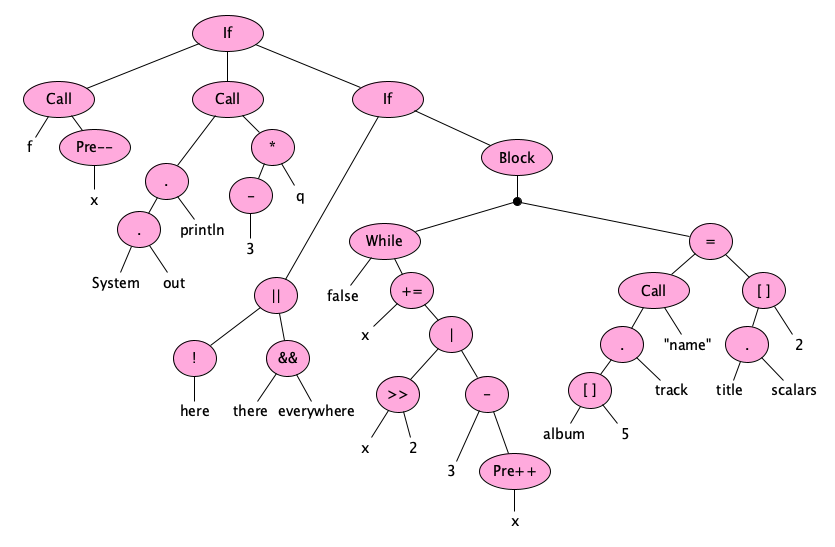
Getting a good feel for abstract syntax naturally takes practice. Here are a couple examples to study to get a feel for how abstract we need to get. Here’s a fragment of Java:

if (((f(--x)))) {
    System.out.println(- 3*q);
} else if (!here||there    &&everywhere) {
    while (false) {
        x += x >> 2 | 3  -++  x;
    }
    album[5].track("name") = title.scalars[2];
}

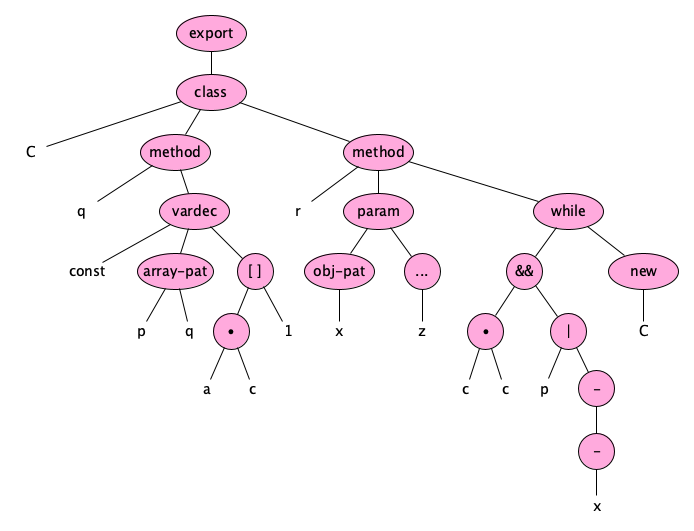
And here’s a little JavaScript program:

export class C {
  q() { const [p, q] = a.c[1]}
  r({x}, ...z) { while (c.c&&p|- -x) new C() }
}

Exploring Abstract Syntax

I’ve built an interactive application for you to explore JavaScript abstract syntax trees. Please try it out!. Hopefully you can get a sense of the connection between concrete and abstract syntax by doing so.

Syntax in the Real World

These notes were very much just an introduction to some of the theory surrounding syntax and syntax definitions. There is so much more to study. For example, you would do well to see how much work goes into writing a grammar for a real-world programming language. Here are a few to check out. Note the wide variety of notations:

• Python
• Java
• JavaScript
• Kotlin
• Go
• Swift
• C++
• C

Alternate Syntactic Descriptions

Hey, before we finish up, there’s one last thing to cover.

So far, we’ve seen two approaches to syntax definition: Syntax Diagrams and a form of analytic grammar based strongly on Parsing Expression Grammars. It turns out there are dozens of published notations out there! You can use whatever you like, but there are some standardized forms that you should be aware of. The following four (CFG, BNF, EBNF, ABNF) are historically significant and very good to know. (You might even be expected to know these if you have a Computer Science degree.)

These notations may not be as formal as you think!

These traditional syntax notations generally do not make distinctions between the lexical and phrase syntaxes. You have to infer by context, or by side notes in a language definition, how tokens are formed and where spaces are allowed to go.

This is why you should stick to analytic grammars!

Context-Free Grammars

Chomsky discovered (or invented?) his Type-2 grammars, which he called Context-Free Grammars, as a minimalistic formalism for studying languages that do not have context. They are by design very “mathematical” and far too low-level to be used in real life. They just use individual symbols. They have no special operators for alternation or repetition. They are too hard to read and are never used directly in practice. A CFG is a 4-tuple $(V,\Sigma,R,S)$, where $V$ is the set of variables, $\Sigma$ is the alphabet (of symbols in the language), $V \cap \Sigma = \varnothing$, $R \subseteq V \times (V \cup \Sigma)*$ is the rule set, and $S \in V$ is the start symbol. For the language of simple arithmetic expressions over natural numbers, a CFG is:

$\begin{array}{l}( \\ \;\;\; \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, *, /, (, )\}, \\ \;\;\; \{E, T, F, N, D\}, \\ \;\;\; \{ \\ \;\;\;\;\;\;\; (D, 0), (D, 1), (D, 2), (D, 3), (D, 4), (D, 5), (D, 6), \\ \;\;\;\;\;\;\; (D, 7), (D, 8), (D, 9), (N, D), (N, ND), (E, T), (E, E+T), \\ \;\;\;\;\;\;\; (E, E-T), (T,F), (T, T*F), (T, T/F), (F,N), (F, (E)) \\ \;\;\; \}, \\ \;\;\; E \\ )\end{array}$

Rather than writing them in tuple form, we often just list the rules, making sure the start symbol appears first, and making the variables and alphabet symbols inferrable by context:

E → E + T
E → E - T
E → T
T → T * F
T → T / F
T → F
F → ( E )
F → N
N → N D
N → D
D → 0
D → 1
D → 2
D → 3
D → 4
D → 5
D → 6
D → 7
D → 8
D → 9

A pure CFG is a super-minimal notation great for studying properties of formal, made-up, simple, languages. But when defining the syntax of real languages we want more expressiveness! It’s nice to have ways to specify things like keywords and spacing, which get super messy if you stick to the pure CFG notation.

BNF

With BNF, we add the ability to have our variables and alphabet symbols be written in a more readable form. To distinguish the two, we quote the variables with angle brackets. One special operator, | (meaning “or”), is permitted.

<expression> ::= <term>
              |  <expression> + <term>
              |  <expression> - <term>
<term>       ::= <factor>
              |  <term> * <factor>
              |  <term> / <factor>
<factor>     ::= <number>
              |  ( <expression> )
<number>     ::= <digit> | <number> <digit>
<digit>      ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Better than a CFG, but there’s still not built-in way to do keywords and spaces.

EBNF

EBNF, or Extended Backus Naur Form, quotes the alphabet symbols instead of the variables, and adds operators for alternation (|), optionality (?), zero-or-more (*), and one-or-more (+).

EXP    = TERM (('+' | '-') TERM)*
TERM   = FACTOR (('*' | '/') FACTOR)*
FACTOR = NUMBER | '(' EXP ')'
NUMBER = ('0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9')+

Now we’re getting more concise. Pure EBNF still doesn’t have any mechanism for distinguishing lexical and phrase variables, so folks using EBNF will either write two grammars (one for the tokens, and one for the phrases), or use some other convention.

ABNF

ABNF, or Augmented Backus Naur Form, is the specification used to describe all the Internet Protocols. It features tools for repetition, alternatives, order-independence, and value ranges.

exp    = term *(("+" / "-") term)
term   = factor *(("*" / "/") factor)
factor = number / "(" exp ")"
number = %x30-39

Recall Practice

Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.

1. What are the utterances of a programming language called?
   Programs
2. What is syntax and how does it differ from semantics?
   Syntax is a specification of the structure of a language, while semantics specifies its meaning.
3. What are some spectra of syntactic forms in common programming languages?
   Pictures vs. text
   Symbols vs. words
   Whitespace significance vs. insignificance
   Indentation vs. curly braces vs. ends vs. parentheses
   Prefix vs. infix vs. postfix
4. What does a syntax diagram for a function call look like, assuming the function being called must be a simple identifier?
5. What does the syntax diagram for a typical floating-point literal look like?
6. What are entities and identifiers?
   An entity is something that is manipulated by a program, such as a variable, literal, function, class, or module. An identifier is a name you can bind to an entity.
7. What is the difference between a statement and an expression?
   An expression is a construct that evaluates to a value, while a statement is a construct that performs an action.
8. What do we call words that look like identifiers but cannot be used as identifiers?
   Reserved words
9. What is a reserved word?
   A token that has the same lexical structure as an identifier but is not allowed to be used as one.
10. How do we, when defining a syntax, make sure reserved words cannot be used as identifiers?
    We start the rule for identifiers with a negative lookahead for reserved words. Also, we need a negative lookahead after each reserved word to make sure it doesn’t prohibit identifiers that may have a reserved word as a proper prefix.
11. What is the difference between the lexical and phrase syntax?
    The lexical syntax defines how individual characters are grouped into words, called tokens (such as identifiers, numerals, and punctuation); the phrase syntax groups words into higher level constructs (such as expressions and statements). These words can be separated by whitespace.
12. Why do grammars make a distinction between lexical and phrase syntaxes? Give two reasons.
    1. To avoid littering nearly every rule with whitespace sequences.
    2. To conceptually simplify the syntax, breaking it down into two manageable parts.
13. What convention are we using on this page to distinguish lexical and phrase variables?
    Lexical variables begin with a lowercase letter; phrase categories begin with an uppercase letter.
14. What exactly is a token?
    A primitive element for a grammar’s phrase structure, e.g., a keyword, identifier, numeric literal, boolean literal, simple string literal (without interpolation), or symbol.
15. What happens during tokenization? What kinds of language constructs are “eliminated” in this process?
    Characters in the source code are grouped into tokens. Comments and spaces between tokens are dropped. Spaces within string literals are kept of course.
16. Where do we generally cut off a parse tree?
    At the token level.
17. What does it mean for a grammar to be ambiguous? Answer in precise, technical terms.
    A grammar is ambiguous if there exists a string that has two distinct derivation trees in the grammar.
18. What kind of rule is a major source of ambiguity, one that is common for beginners to write?
    Rules with multiple components the same as the category being defined, e.g., $exp \longrightarrow exp\;op\;exp\;\mid\;\cdots$
19. How is operator precedence captured in a language definition?
    We use multiple syntactic categories for expressions; for example Expression, Term, Factor, Primary.
20. How do we capture the conventional precedences and associativities of binary arithmetic operators in an analytic grammar?
    $\begin{array}{lcl} \mathit{Exp} & \longleftarrow & (\mathit{Exp} \; \mathit{addop})? \; \mathit{Term} \\ \mathit{Term} & \longleftarrow & (\mathit{Term} \; \mathit{mulop})? \; \mathit{Factor} \\ \mathit{Factor} & \longleftarrow & \mathit{Primary} \; (\texttt{"**"} \; \mathit{Factor})? \\ \end{array}$
21. What is a good way to treat the expression -3**2 in a language definition?
    It should be made illegal by the grammar! This eliminates the possible confusion about whether it means (-3)**2 or -(3**2), since it requires programmers to use parentheses.
22. What kinds of rules about program legality are not context free? Find as many as you can.
    Some of them are:

    • Type checking
    • Redeclaration of identifiers within a scope
    • Use of an undeclared identifier
    • Matching arguments to parameters in a call
    • Access checks (public, private, etc.)
    • Identifiers must be used in all paths through their scope
    • A return must appear in all paths through a function
    • Pattern match exhaustiveness
    • In a subclass, abstract methods must be implemented or declared abstract
    • All private functions must be called within a module

    There may be more.
23. What are two formalisms that have been created to capture context-sensitive rules?
    Attribute Grammars and Two-Level Grammars
24. What do many language designers do in order to avoid the complexity of context-sensitive grammar rules?
    They push the rules into the world of semantics.
25. What kinds of rules about program legality can in principle be captured in a context-free syntax, but are generally not so captured in practice because the the required complexity of the rules?
    • Requiring break and continue in a loop (as this would require difference classes of statements)
    • Requiring return in a function body (as this would require difference classes of statements)
    • Enforcing ranges on certain numeric types.
26. In principle, can you capture the notion at all integer literals (in a hypothetical language) must be between -2147483648 and 2147483647? If so, why don’t we?
    Yes, you certainly can, but the resulting specification is ugly af and really hard to decipher and understand.
27. Draw the parse tree and the abstract syntax tree for the expression 8 * (13 + 5), assuming a grammar with categories named Exp, Term, Factor, Primary, and num.
    The parse tree is:

              Exp
               |
             Term
           /   |   \
      Term     *    Factor
       |           /   |   \
     Factor       (   Exp   )
       |            /  |  \
    Primary      Exp   +   Term
       |          |          |
      num       Term       Factor
                  |          |
               Factor     Primary
                  |          |
               Primary      num
                  |
                 num
    

    The abstract syntax tree is:

          *
        /   \
      8      +
            /  \
          13    5
    

28. Is indentation-sensitivity context-free?
    No
29. What is a concrete syntax?
    A precise specification of which strings (sequences of characters) are structurally legal programs.
30. What kinds of constructs appear in a concrete syntax but not in an abstract syntax? See how many items you can find.
    • Punctuation and delimiters
    • Intermediate expression categories, e.g. Exp1, Exp2, Term, Factor, ...
    • INDENT and DEDENT tokens
31. Given the expression 8 * (13   + 5), how many source code characters are there? When tokenized, how many tokens are there? How many nodes are there in the abstract syntax tree?
    14 characters, 7 tokens, 5 nodes.
32. What kind of formal notation can capture an abstract syntax?
    A tree grammar.
33. What does the tree grammar for Astro look like?
    $\begin{array}{lcl} n: \mathsf{Nml} & & \\ i: \mathsf{Ide} & & \\ e: \mathsf{Exp} & = & n \mid i \mid -e \mid e+e \mid e-e \mid e\,\mathtt{*}\,e \mid e\,/\,e \mid e\,\mathtt{**}\,e \mid i\;e^*\\ s: \mathsf{Stm} & = & i = e \mid \mathtt{print}\;e\\ p: \mathsf{Pro} & = & \mathtt{program}\;s^+\\ \end{array}$
34. What does the AST for the JavaScript expression while (x - 3 === y) { drop(p[5].q) } look like?

             while
            /      \
         ===        call
         / \       /    \
        -   y   drop     .
      /  \             /   \
    x     3          []     q
                    /  \
                   p    5
    

35. What are some notations that have been used to specify the syntax of programming languages?
    BNF, EBNF, ABNF.
36. What syntax notation is used for official Internet standards?
    ABNF

Summary