Language Theory
Why?
Why would we ever even want a theory of languages?
Languages are all about how we represent and communicate information and computations. A formal theory of language allows us to rigorously define what language is, and from that we can show exactly what various languages can represent and say.
Preliminaries
Theories of computation, including language theory, start from the idea that information can be represented as a string of symbols.
Information is that which informs. In information theory, it is the resolution of uncertainty. The more you know, the less uncertain you are.
Information theory and language theory both use a fair amount of logical and mathematical notation. If you need to brush up, see these logic notes and these math notes.
Symbols
A symbol is a primitive unit of data representation. Information can be represented with strings of symbols. For example:
91772.3e-8Stay behind the yellow line!ᐊᐃᖓᐃ ᓄᓇᕐᔪᐊᖅ/Pecs/Los Angeles/Berlin/Madrid//1 2/3 0/2 2/2 0/3 2///(* (+ 4 3) (- 9 7))int average(int x, int y) {return (x + y) / 2;}<dog id="30024"><name>Lisichka</name><age>13</age></dog>{"type": "dog", "id": "30024", "name": "Lisichka", "age": 13}∀α β. α⊥β ⇔ (α•β = 0)1. f3 e5 2. g4 ♛h4++
Alphabets
Symbols are chosen from an alphabet, such as $\{0,1,2,3,4,5,6,7,8,9\}$ for the language of natural numbers, or $\{0,1,2,3,4,5,6,7,8,9,.,\textrm{e},\textrm{E},+,-\}$ for the language of floating-point numbers.
Here are some examples of alphabets:
- $\mathsf{BinaryDigits} = \{ 0, 1 \}$
- $\mathsf{DecimalDigits} = \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \}$
- $\mathsf{HexDigits} = \mathsf{DecimalDigits} \cup \{ a,b,c,d,e,f,A,B,C,D,E,F \}$
- $\mathsf{Suits} = \{ ♠️,♥️,♦️,♣️ \}$
- $\mathsf{PropositionalLogicSymbols} = \{ p, q, r, \prime, (, ), \neg, \wedge, \vee, \supset, \equiv \}$
- $\mathsf{Unicode} = \{ \sigma \mid \sigma \textrm{ is a Unicode character} \}$
Strings
A string is a finite sequence of symbols over some alphabet.
Examples: For the alphabet $\{a,b,c\}$, three example strings are: $abbcbabb$, $b$, $aaa$.
When talking about strings, we might use variables to represent them. In this case the variable names should be, necessarily, outside the alphabet:
Examples: $w = abbcbabb$, $x = b$, $y = aaa$.
The length of a string is the number of symbol occurrences in the string.
Example: if $w = abbac$, then $|w| = 5$.
The empty string, denoted $\varepsilon$, is the (unique) string of length 0.
The concatenation of two strings $x$ and $y$ is the string obtained by appending $y$ to the end of $x$. We have a notation for repeated concatenation: $w^0 = \varepsilon$, $w^1 = w$, $w^2 = ww$, and $w^{k+1} = ww^k$.
Example: if $x = abb$ and $y = ca$ then $xy = abbca$.
Example: $w\varepsilon = \varepsilon w = w$.
Example: $(abc)^4 = abcabcabcabc$.
Tricky Notation?String concatenation looks like numeric multiplication, and string repetition looks like numeric exponentiation, but behaviorally, concatenation is like numeric addition and repetition is like numeric multiplication. If you’ve programmed in Python, you’ll see that is indeed true.
$ python >>> "abc" + "def" 'abcdef' >>> "abc" * 3 'abcabcabc'Guido got it right.
The reversal $w^R$ of a string $w$ is the string formed by reversing $w$; formally $\varepsilon^R = \varepsilon$ and $(\sigma w)^R = w^R \sigma$ for some symbol $\sigma$.
$x$ is a substring of $y$ iff $\exists v. \exists w. y = vxw$.
Because we are defining languages with an eye toward modeling computation, we almost always require alphabets to be non-empty and finite, and require all strings to have a finite (but unbounded) length. Even with a finite alphabet and finite-length strings, you can still have an infinite number of strings!
Example: The finite alphabet $\{0,1\}$ gives rise to the infinite number of strings $0$, $1$, $00$, $01$, $10$, $11$, $000$, $001$, etc.
Formal Languages
A formal language is a set of strings over some alphabet. That’s it. That’s the definition. If a string $w$ is a member of a language $L$ we say $w$ is an utterance of $L$.
Examples
Examples first! Here are some example languages:
- $\{ w \in \{ a, b \}^* \mid w \textrm{ has the same number of $a$’s as $b$’s} \}$
- $\{ w \in \{ a, b \}^* \mid w \textrm{ has more $a$’s than $b$’s} \}$
- $\{ w \in \{ a, b \}^* \mid \textrm{the first and last symbol of $w$ are the same} \}$
- $\{ a^nb^n \mid n \geq 0 \}$
- $\{ a^ib^j \mid j = 2^i \}$
- $\{ a^ib^jc^k \mid k = i + j \}$
- $\{ ww \mid w \in \{a,b\}^* \}$
- $\{ ww^R \mid w \in \{a,b\}^* \}$
- $\{ 1^n \mid \textrm{$n$ is prime} \}$
- $\{ w \in \{ 0, 1 \}^* \mid w \textrm{ is a binary numeral greater than 55} \}$
- $\{ w \in \{ 0, 1 \}^* \mid w \textrm{ is a binary numeral divisible by 5} \}$
- $\{ w \in \textsf{DecimalDigit}^* \mid w \textrm{ is a valid MasterCard number} \}$
- $\{ w \in \mathsf{Unicode}^* \mid w \textrm{ contains the substring } \textit{dog} \}$
- $\{ w \in \mathsf{Unicode}^* \mid w \textrm{ is a valid Python program} \}$
- $\{ w \in \mathsf{Unicode}^* \mid w \textrm{ is a valid JavaScript program} \}$
- $\{ w \in \mathsf{Unicode}^* \mid w \textrm{ is a valid Swift program} \}$
- $\{ w \in \mathsf{Unicode}^* \mid w \textrm{ is a valid Swift program that prints the integers from 1 to 10} \}$
Why are languages sets?A language as a set of strings is actually quite useful. It distinguishes strings “in” the language from those not in the language. A language is a set of (legal) utterances.
Now it’s true that this definition does not say anything about the “meaning” of each utterance. That has to be handled separately. But we are off to a good start.
Language Operations
Because languages are sets, $\varnothing$ is a language, and the union ($L_1 \cup L_2$) and intersection ($L_1 \cap L_2$) of languages make perfect sense. So does the cardinality of a language, $|L|$, the number of strings in the language. In addition:
- The concatenation of two languages $L_1$ and $L_2$ is $L_1L_2 = \{xy \;|\; x \in L_1 \wedge y \in L_2\}$. Also, we define $L^0 = \{\varepsilon\}$, $L^1 = L$, $L^2 = LL$, $...$, $L^{k+1} = LL^k$.
- The Kleene Closure of $L$ is $L^* = L^0 \cup L^1 \cup L^2 \cup ... = \{w_1w_2...w_k \;|\; w_i \in L \wedge k ≥ 0\}$.
- The Positive Closure of $L$ is $L^+ = L^1 \cup L^2 \cup L^3 \cup ... = \{w_1w_2...w_k \;|\; w_i \in L \wedge k > 0\}$.
Therefore, given an alphabet $\Sigma$, the following are languages over $\Sigma$:
- $\varnothing$, the empty language, the language of no strings
- $\{ \varepsilon \}$, the language containing the empty string and nothing else
- $\Sigma$, the language of all possible one-symbol strings
- $\Sigma^2$, the language of all possible two-symbol strings
- $\Sigma^3$, the language of all possible three-symbol strings
- $\Sigma^*$, the language of all possible strings over the alphabet $\Sigma$
The Infinite Library
The language $\Sigma^*$ (the language of all possible strings over an alphabet) is fascinating. It’s basically the infinite library, which contains every book that has ever been written and that could possibly ever be written, i.e., every single possible arrangement of symbols. It contains solutions to climate change and world hunger, the cures for all cancers, and all human histories and futures (yours included). It also contains an infinite amount of misinformation. The problem is, you can’t distinguish what is right from wrong.
When you “know” everything, you know nothing.
For any language $L$ over the alphabet $\Sigma$, we have $L \subseteq \Sigma^*$. Since we must specify an alphabet for each language, the complement of a language makes sense. It is defined as follows: $\overline{L} = \Sigma^* - L$
Let’s see the language operations in use. Suppose we are given the alphabet $\Sigma = \{a,b\}$, and two languages over $\Sigma$, which we’ll define as $L_1 = \{ba, b\}$ and $L_2 = \{abb, bb\}$.
Then:
- $\Sigma^* = \{\varepsilon,a,b,aa,ab,ba,bb,aaa,aab,aba,abb,baa,bab,...\}$
- ${L_1}^* = \{\varepsilon,ba,b,baba,bab,bba,bb,...\}$
- ${L_1}^+ = \{ba,b,baba,bab,bba,bb,...\}$
- $L_1L_2 = \{baabb, babb, bbb\}$
- $L_1 \cup L_2 = \{ba, b, abb, bb \}$
- $L_1 \cap L_2 = \varnothing$
Random Language Facts
Here are some interesting theorems about languages. Ready? Let $\Sigma$ be an alphabet and $A$, $B$, $C$, and $D$ be languages over $\Sigma$ (i.e., subsets of $\Sigma^*$). Then:
- $A\varnothing = \varnothing A = \varnothing$
- $A\{\varepsilon\} = \{\varepsilon\}A = A$
- $(AB)C = A(BC)$
- $(A \subseteq B) \wedge (C \subseteq D) \Rightarrow AC \subseteq BD$
- $A(B \cup C) = AB \cup AC$
- $(B \cup C)A = BA \cup CA$
- $A(B \cap C) \subseteq AB \cap AC$
- $(B \cap C)A \subseteq BA \cap CA$
- $A^* = A^+ \cup \{\varepsilon\}$
- $n ≥ 0 \Rightarrow A^n \subseteq A^*$
- $n ≥ 1 \Rightarrow A^n \subseteq A^+$
- $A \subseteq AB^*$
- $A \subseteq B^*A $
- $A \subseteq B \Rightarrow A^* \subseteq B^*$
- $A \subseteq B \Rightarrow A^+ \subseteq B^+$
- $AA^* = A^*A = A^+$
- $\{\varepsilon\} \in A$ iff $A^+ = A^*$
- $(A^*)^* = A^*A^* = A^*$
- $(A^*)^+ = (A^+)^* = A^*$
- $A^*A^+ = A^+A^* = A^*$
- $(A^*B^*)^* = (A \cup B)^* = (A^* \cup B^*)^*$
- $(C = AC \cup B) \Rightarrow (C = A^*B)$
Language Definition
Formal languages were developed to help us study the foundations of mathematics and computation. It’s true that in this context, languages are just sets, so we can communicate them in set notation, for example:
- $\{ w \mid w \textrm{ is a legal floating point numeral} \}$
But wait, even though that definition used mathematical symbols in part, there was a big informal piece between the curly braces. This can be a problem. Informal definitions lack precision. Like what even are floating point numerals? We can list as many examples as possible to get the idea. Maybe we can list them all, say something like { 0, 8, 3.5, 13.55, 3E8, 3.2E89, 5.111E+2, 21.34E-2, 1e-8, 2.55e+233, ...}. This is also not precise. Let’s try harder, with a definition:
- The set of all strings that begin with a sequence of one or more decimal digits,
- optionally followed by a dot then one or more decimal digits
- optionally followed by:
- an
Eor ane - then, optionally, a
+or- - then a sequence of one or more decimal digits
- an
Also not very satisfying: it is very verbose, kind of confusing, and hard to tell if it is even right. It is “precise” but it is still informal ! We need something better. Something formal. As it happens, we can do this! There are two major approaches:
- Definition by Generation
- We can give a formalized set of rules that systematically generate all and only those strings in the language. The language is then the set of all string generated by the language.
- Definition by Recognition
- We can give a formal definition of a process that determines, for a given string, whether or not it is in the language. The language is then the set of all strings recognized by the process.
Language Generation
The primary mechanism to define a language via generation is the generative grammar.
Generative Grammars
A generative grammar is a list of rules that generates all and only those strings in a particular language. The rules have variables that get replaced in order to generate the actual strings of the language. Here’s a grammar for our floating point numeral language. The alphabet for this language is $\{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ., E, e, +, – \}$. Our grammar will use four variables, $\{ \mathit{numeral}, \mathit{fractionalPart}, \mathit{exponentPart}, \mathit{digit} \}$:
$ \begin{array}{lcl} \mathit{numeral} & \longrightarrow & \mathit{digit}^+ \; \mathit{fractionalPart}? \; \mathit{exponentPart}?\\ \mathit{fractionalPart} & \longrightarrow & \texttt{"."} \; \mathit{digit}^+ \\ \mathit{exponentPart} & \longrightarrow & (\texttt{"E"} | \texttt{"e"}) \; (\texttt{"+"} | \texttt{"–"})? \;\mathit{digit}^+ \\ \mathit{digit} & \longrightarrow & \texttt{"0"} .. \texttt{"9"} \end{array} $
There are multiple grammar notations out there; the one used here features the following notation:
→means “can be replaced with”+means “one or more”*means “zero or more”?means “optional”|means “or”- Double quotes delimit the actual symbols in the language you are defining, while variables are unquoted
- Parentheses are for grouping
..makes a range over individual symbols (yeah, it’s kind of shorthand)
If $G$ is a grammar, then $L(G)$ is the language defined by the grammar $G$. A string is in $L(G)$ if it is derivable from $G$’s initial rule, repeatedly replacing instances of a rule’s left hand pattern with its right hand side, until you get completely rid of the variables and are left only with strings in the language’s alphabet. Here is an example derivation:
$ \begin{array}{lcl} \mathit{numeral} & \Longrightarrow & \mathit{digit}^+\;\mathit{fractionalPart}?\;\mathit{exponentPart}? \\ & \Longrightarrow & \texttt{338}\;\mathit{fractionalPart}?\;\mathit{exponentPart}? \\ & \Longrightarrow & \texttt{338.}\;\mathit{digit}^+\;\mathit{exponentPart}? \\ & \Longrightarrow & \texttt{338.253}\;\mathit{exponentPart}? \\ & \Longrightarrow & \texttt{338.253}\;(\texttt{"E"} | \texttt{"e"}) \; (\texttt{"+"} | \texttt{"–"})? \;\mathit{digit}^+ \\ & \Longrightarrow & \texttt{338.253e}\;(\texttt{"+"} | \texttt{"–"})? \;\mathit{digit}^+ \\ & \Longrightarrow & \texttt{338.253e}\;\mathit{digit}^+ \\ & \Longrightarrow & \texttt{338.253e18} \\ \end{array} $- 3
- 8.5501e-88
- 5E+11
and that the following are not in the language:
- -2.3E1
- 55.e+2
- ^^Dog!
By the way, note that there can be many grammars that specify the same language. For example, here’s another grammar for the floating-point numeral language:
$ \begin{array}{lcl} \mathit{numeral} & \longrightarrow & \mathit{digit}^+ \; (\texttt{"."} \; \mathit{digit}^+)? \; ((\texttt{"E"} | \texttt{"e"}) \; (\texttt{"+"} | \texttt{"–"})? \;\mathit{digit}^+)?\\ \mathit{digit} & \longrightarrow & \texttt{"0"} .. \texttt{"9"} \end{array} $
If the first grammar above was called $G_1$ and this grammar was called $G_2$, we would have $L(G_1) = L(G_2)$.
Practice with Grammars
If you think about it, coming up with a grammar for a language you have in mind is an endeavor similar to programming: you know what you want to end up with, but you need to create the very formal, precise steps to get you there. How do you get good at coming up with grammars? Certainly it helps to have a mentor and learn tricks of the trade over time with practice. Whether you have a mentor or not, it does help to start with a whole bunch of examples. So with that in mind, here are a handful of grammars for you to study:
The language of integer binary numerals divisible by 2:
$\begin{array}{lcl} \mathit{even} & \longrightarrow & \texttt{"–"}?\;(\texttt{"0"}\,|\,\texttt{"1"})^* \; \texttt{"0"} \\ \end{array}$
The language of integer decimal numerals divisible by 5:
$\begin{array}{lcl} \mathit{divisibleByFive} & \longrightarrow & \texttt{"–"}?\;\mathit{digit}^*\;(\texttt{"0"}\,|\,\texttt{"5"}) \\ \mathit{digit} & \longrightarrow & \texttt{"0"} .. \texttt{"9"} \end{array}$
The language $\{ \varepsilon, 0, 1, 01, 10, 010, 101, 0101, 1010, \ldots\}$ of alternating zeros and ones:
$\begin{array}{lcl} \mathit{alternating} & \longrightarrow & \mathit{startsWithZero} \;|\; \mathit{startsWithOne} \\ \mathit{startsWithZero} & \longrightarrow & \varepsilon\;|\;\texttt{"0"}\;\mathit{startsWithOne} \\ \mathit{startsWithOne} & \longrightarrow & \varepsilon\;|\;\texttt{"1"}\;\mathit{startsWithZero} \end{array}$
The language $\{0^i1^j \mid i \textrm{ is even} \wedge j \textrm{ is odd} \}$:
$\begin{array}{lcl} \mathit{evenZerosThenOddOnes} & \longrightarrow & (\texttt{"00"})^*\;\texttt{"1"}\;(\texttt{"11"})^* \end{array}$
The language $\{ a^nb^n \mid n \geq 0 \}$ = $\{ \varepsilon, ab, aabb, aaabbb, aaaabbbb, \ldots\}$:
$\begin{array}{lcl} \mathit{anbn} &\longrightarrow & \varepsilon \mid \texttt{"a"}\;\mathit{anbn}\;\texttt{"b"} \end{array}$
The language of palindromes over $\{a,b\}$:
$\begin{array}{lcl} \mathit{pal} & \longrightarrow & \varepsilon \;|\;\texttt{"a"}\;|\;\texttt{"b"}\;|\;\texttt{"a"}\;\mathit{pal}\;\texttt{"a"}\;|\;\texttt{"b"}\;\mathit{pal}\;\texttt{"b"} \\ \end{array}$
The language of parentheses, curly braces, and square brackets, in which everything is properly balanced and nested, for example ()[{()}[[]]()]:
$\begin{array}{lcl} \mathit{balanced} & \longrightarrow & (\texttt{"("}\;\mathit{balanced}\;\texttt{")"}\mid\texttt{"["}\;\mathit{balanced}\;\texttt{"]"}\mid\texttt{"\{"}\;\mathit{balanced}\;\texttt{"\}"})^*\\ \end{array}$
The language $\{ a^nb^nc^n \mid n \geq 0 \}$:
$\begin{array}{lcll} \mathit{s} & \longrightarrow & \varepsilon \mid \texttt{"a"}\;s?\;x\;\texttt{"c"} & \\ \texttt{"c"}\;x & \longrightarrow & x\;\texttt{"c"} & \textrm{—move $c$'s to the right of the $x$'s} \\ \texttt{"a"}\;x & \longrightarrow & \texttt{"ab"} & \textrm{—only make a $b$ after an $a$ ...} \\ \texttt{"b"}\;x & \longrightarrow & \texttt{"bb"} & \textrm{—... or after a $b$} \end{array}$
The language $\{ a^{2^n} \mid n \geq 0 \}$:
$\begin{array}{lcll} \mathit{aToTwoToN} & \longrightarrow & \mathit{double}^*\;\texttt{"a"}\;\mathit{right} & \textrm{—mark the end} \\ \mathit{double}\;\texttt{"a"} & \longrightarrow & \texttt{"aa"}\;\mathit{double} & \textrm{—move right, doubling $a$'s as you go} \\ \mathit{double}\;\mathit{right} &\longrightarrow & \mathit{right} & \textrm{—got to end, no more to double} \\ \mathit{right} & \longrightarrow & \varepsilon \\ \end{array}$
The language $\{ww \mid w \in \{a,b\}^* \}$:
$\begin{array}{lcll} \mathit{s} & \longrightarrow & \texttt{"a"}\;s\;x \mid \texttt{"b"}\;s\;y \mid \mathit{middle} & \\ \mathit{middle}\;x & \longrightarrow & \mathit{middle}\;\texttt{"a"} & \textrm{—an $x$ generates an $a$} \\ \mathit{middle}\;y & \longrightarrow & \mathit{middle}\;\texttt{"b"} & \textrm{—a $y$ generates a $b$} \\ \texttt{"a"}\;x & \longrightarrow & x\;\texttt{"a"} & \textrm{—move $a$'s to end} \\ \texttt{"a"}\;y & \longrightarrow & y\;\texttt{"a"} & \\ \texttt{"b"}\;x & \longrightarrow & x\;\texttt{"b"} & \textrm{—move $b$'s to end} \\ \texttt{"b"}\;y & \longrightarrow & y\;\texttt{"b"} & \\ \mathit{middle} & \longrightarrow & \varepsilon & \textrm{—drop midmarker when no longer needed} \\ \end{array}$
Why are we studying such silly languages?
Obviously we need to get to the point where we can design grammars for real programming languages. But studying the fundamentals of language and grammars with bite-size pieces helps us uncover patterns that we can use in designing our large grammars. It also gives insights into what is easy and what is hard. For example: some grammars above looked very straightforward and some required bizarre “marker” symbols that were passed around to...“compute” something it seems. The scientist in you should wonder if distinctions like that are fundamental in some sense, and if so, how can we capture this state of affairs formally.
We are going to do lots of derivations for many of the grammars above.
More Example Grammars
You can’t have too many examples, so let’s see more. To help us out a bit, we’re going to take the following variables a being previously defined:
- $\mathit{digit}$, for $\texttt{"0".."9"}$
- $\mathit{hexDigit}$, for $\mathit{digit}\;|\;\texttt{"A".."F"}\;|\;\texttt{"a".."f"}$
- $\mathit{letter}$, for any Unicode letter
- $\mathit{alnum}$, for $\mathit{letter}\;|\;\mathit{digit}$
Here is the language of words starting with a letter and containing letters, digits, and underscores only:
$\begin{array}{lcl} \mathit{id} & \longrightarrow & \mathit{letter}\;(\mathit{alnum}\;|\;\texttt{"_"})^* \end{array}$
The language of simple hex colors in HTML: Hash followed by 3 or 6 hex digits:
$\begin{array}{lcl} \mathit{simpleHexColor} & \longrightarrow & \texttt{"#" }\mathit{threeHexDigits}\;\mathit{threeHexDigits}? \\ \mathit{threeHexDigits} & \longrightarrow & \mathit{hexDigit}\;\mathit{hexDigit}\;\mathit{hexDigit} \end{array}$
Now let’s create a language for integer expressions with addition, subtraction, multiplication, division, exponentiation, negation, and parentheses. When languages start to get complex, it helps to see examples and non-examples:
| Examples | Non-Examples |
|---|---|
432 24*(31/899+3-0)/(54/-2+(5+2)*3) (2) 8*(((3-6))) |
43 2 24*(31////)/(5+---+)) [fwe]23re31124efr$#%^@ --2-- |
Here is a first pass. We say: “An expression is either (1) an integer, (2) a negated expression, (3) two expressions with a binary operator between them, or (4) a parenthesized expression.” This gives us:
$\begin{array}{lcl} \mathit{exp} & \longrightarrow & \mathit{digit}^+ \\ & | & \texttt{"–"} \; \mathit{exp} \\ & | & \mathit{exp} \; (\texttt{"+" | "–" | "*" | "/" | "%" | "**"}) \; \mathit{exp} \\ & | & \texttt{"(" }\mathit{exp}\texttt{ ")"} \end{array}$
How did we do? Let’s see if we can derive something interesting:
$ \begin{array}{lcl} \mathit{exp} & \Longrightarrow & \mathit{exp}\texttt{ + }\mathit{exp} \\ & \Longrightarrow & \texttt{– }\mathit{exp}\texttt{ + }\mathit{exp} \\ & \Longrightarrow & \texttt{– }\mathit{digit}\texttt{ + }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+ }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+ }\mathit{exp}\texttt{ * }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+ }\mathit{digit}\;\mathit{digit}\texttt{ * }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+5}\;\mathit{digit}\texttt{ * }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+55* }\mathit{exp} \\ & \Longrightarrow & \texttt{–8+55* }\mathit{digit} \\ & \Longrightarrow & \texttt{–8+55*3} \\ \end{array}$Derivations can get pretty long. Is there a better way to see how our strings are made?
Derivation Trees
Here’s a better way to “show” the derivation we just performed:
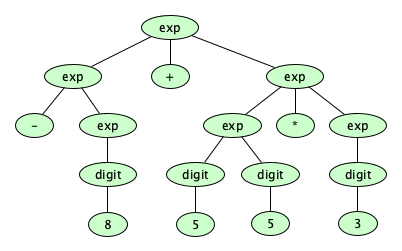
But wait! There can be more than one way to derive a string, and sometimes (but not always) the resulting derivation tree is different for different derivations:
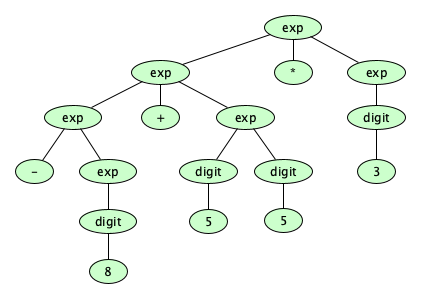
-5*(34/-55+(21-8)+233). How many distinct trees are there for this string?
Is having multiple derivation trees for a string a big deal?
Ambiguity
A grammar is ambiguous if there exists more than one derivation tree for a given string. Natural language grammars are often ambiguous.
- Lawyers give poor free advice.
- Teacher strikes idle kids.
- Seven foot doctors sue hospital.
- Stolen painting found by tree.
- Enraged cow injures farmer with ax.
- Two sisters reunited after 18 years at checkout counter.
- The train left the station crowded and dirty.
- Landmine claims dog arms company.
- Hershey bars protest.
- They cooked for the first time on the stove.
But for a programming language, we don’t really like ambiguity, since the derivation tree tells us the structure of a program (its syntax) from which we wish to assign a meaning (semantics). Under the widely accepted meanings of decimal integers and arithmetic operations, those two trees we saw earlier suggest meanings of 157 (multiply-then-add) and 141 (add-then-multiply). Yikes!
One way to get rid of ambiguity in our language is to force operator precedence and associativity in the grammar. The following convention has arisen:
- Expressions are terms separated by left-associative additive operators (
+,-) - Terms are factors separated by left-associative multiplicative operators (
*,/,%) - Factors are primaries separated by right-associative exponentiation operators (
**) - Primaries are numerals, negated primaries, or parenthesized expressions.
Because expressions are made up of terms and terms are made up of factors, the utterance 1+3*2 is made up of two terms, 1 and 3*2. Therefore we say multiplication has higher precedence than addition. This is the only way to make the derivation tree! There is no ambiguity here. Now what about (1+3)*2? This expression has a single term, which has two factors: (1+3) and 2. Note how the parentheses matter!
But what about the utterance 5-1-3? Should this be structured to do the leftmost subtraction first (yielding 1) or the rightmost first (yielding 7)? This is where associativity comes in. Tradition says subtraction is left-associative, so we want a structure with:
–
/ \
– 3
/ \
5 1
Exponentiation is traditionally right-associative, so 3**2**5 would desire a derivation structure as:
**
/ \
3 **
/ \
2 5
Do you know what else might be ambiguous? Expressions like -2**2. In Python, exponentiation is done before negation, so this expression produces -4. In Elm, negation happens first, so the expression evaluates to 4. JavaScript uses a grammar that prevents the expression from being derived by the grammar! This is a good thing. Let’s do it.
We are now ready to give the non-ambiguous grammar for our integer arithmetic expression language:
$ \begin{array}{lcl} \mathit{exp} &\longrightarrow& \mathit{exp} \;(\texttt{"+"}\,|\,\texttt{"–"})\; \mathit{term} \\ & | & \mathit{term} \\ \mathit{term} &\longrightarrow& \mathit{term} \;(\texttt{"*"}\,|\,\texttt{"/"}\,|\,\texttt{"%"})\; \mathit{factor} \\ & | & \mathit{factor} \\ \mathit{factor} &\longrightarrow& \mathit{primary}\;(\texttt{"**"}\;\mathit{factor})? \\ & | & \texttt{"–"}\;\mathit{primary} \\ \mathit{primary} &\longrightarrow& \mathit{numeral} \\ & | & \texttt{"("} \; \mathit{exp} \; \texttt{")"} \\ \mathit{numeral} & \longrightarrow & \mathit{digit}^+ \end{array} $
We are going to make a long-ish expression and show that it has one and only one derivation tree.
-3**2 cannot be derived from this grammar.
The Formal Definition of a Grammar
We’ve seen that we use grammars to formally describe mathematical objects we call languages. But we were kind of hand-wavy in defining what a grammar is and how derivations work. Grammars are mathematical objects themselves and so can be described formally. Here is how:
A grammar is a quadruple $(V, \Sigma, R, S)$ where:
- $\Sigma$ is the alphabet of the language being described
- $V$ is a set of variables, such that $\Sigma \cap V = \varnothing$
- $R \subseteq (V \cup \Sigma)^*V(V \cup \Sigma)^* \times (V \cup \Sigma)^*$ is a set of rules
- $S \in V$ is the start variable
The formal definition of $R$ looks complex but it really just says “the left hand side must contain at least one variable.” That is all. Super reasonable too! It’s there so once you get rid of all the variables, you don’t keep going.
$\{ 0^n1^n \mid n \geq 0 \}$
is formally denoted$(\{s\}, \{0,1\}, \{(s,\varepsilon), (s,0s1)\}, s)$
Please work through this to make sure you “see” it and understand it.Derivations can be formalized too:
As can the language defined by a grammar:
We also use the notation $L(G)$ for the language defined by grammar $G$.
You might be wondering about the|and?and*and+symbols and why they do not appear in our formal definition. As it turns out, they are not needed: they are just shorthands (“syntactic sugar”) for proper rules. We will work out in class exactly how they can be replaced with regular rules.
TerminologyThe page you are reading calls $\,V$ the set of variables and $\,\Sigma$ the alphabet. You may encounter folks who call $\,V$ the set of non-terminals and $\,\Sigma$ the set of terminals. No matter what the names, $\,V \cap \Sigma=\varnothing$.
Well...actually...there are still other folks that call $\,V$ a vocabulary and make it the set of all variables plus the alphabet symbols and consequently tell you now that $\,\Sigma \subset V$.
I know, I know. The moral here is that there ain’t just one way to label all the ideas behind grammars. Different authors describe this stuff differently.
Can grammars be simplified?The development of formal languages originated with early work by Emil Post, Axel Thue, and others working in the early 20th century on questions related to the foundations of mathematics and computation. Post created a system for transforming strings, called a Post Canonical System. We now know a much simpler formulation of Post’s work, namely a semi-Thue system, a.k.a. string rewriting system. An SRS can rewriting any string into any other; it is nothing more than a tuple $(\Sigma, R)$ where $\Sigma$ is the alphabet of symbols and $R \subseteq \Sigma^* \times \Sigma^*$ is the rewriting relation.
That’s it!
However, despite their simplicity, they are rather clunky to use to define languages. Chomsky’s genius move was to add variables, making a special kind of a rewriting system known as a grammar. Brilliant! This is why all computer scientists encounter grammars and only very few have heard of string rewriting systems.
Restricted Grammars
In practice, it is often super-convenient to talk about grammars with restricted rule sets, as these may yield grammars which are much simpler to understand and work with. Of course, you lose the ability to derive as many languages as an unrestricted grammar, but the simplicity might be worth it. There are many dozens of known restricted grammar types, but there are three that you should know: Context-Free, Right-Linear, and Essentially Noncontracting.
Context-Free Grammar
A CFG is a grammar where $R \subseteq V \times (V \cup \Sigma)^*$, that is, the left hand side is just a single variable. So simple and clean, sensible and intuitive. Because of this, they’ve been massively successively successful and the foundation for the vast majority of structural definitions for real programming languages. Interestingly, they aren’t actually powerful enough to capture all legal programs in most programming languages! We’ll see later how to handle this problem in practice.
Why are they called context free?Context-free grammars are so-named because variables can be rewritten regardless of the context in which they appear. (For example, context free grammars would allow say, an expression in a programming language, to be any identifier whatsoever at any time, regardless of whether one is in the context in which the identifier was previously declared or not.)
Right-Linear Grammar
An RLG is a grammar where $R \subseteq V \times (\Sigma^* \cup \Sigma^*V)$, that is, the left hand side is just a single variable and the right hand side is a string of zero or more symbols followed by at most one variable. Pretty interesting: their derivations line up with the idea of a linear computation without memory. More on this later.
Essentially Noncontracting Grammar
In every rule in a ENCG, the right hand side never has fewer symbols and variables than the left hand side—with only one possible exception: if the language contains the empty string, we can have one rule that maps the start symbol to the empty string. The conceptual idea for a noncontracting grammar is that the derivation string never gets shorter; the essentially noncontracting grammars are those that have that one exception to allow for the empty string being in the language. These correspond to computations with bounded memory.
Language Recognition
A grammar lets us formally specify a language by generating all and only those strings in the language. But we can define a language another way: we can give a process that, when given a string, determines whether it belongs to a language?
Hey this is actually very cool! Such a process can be used in a compiler! Let’s learn.
Automata
One way to define a language through recognition is to use automata with accept states. Here is a Turing Machine with an accept state that will accept all and only those strings in the language of even binary numerals:
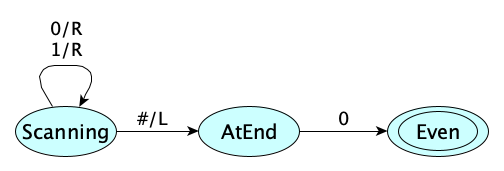
Both the grammar even → ("0"|"1")*"0" and the Turing Machine above “define” the same language, one in a generative fashion and the other in a recognitive fashion. Cool.
But there’s more! Just like we showed several ways to dumb-down restrict grammars for the purpose of generating certain interesting classes of languages, Turing Machines can be restricted in several ways, too, each of which correspond to certain kinds of grammars. (This is either creepy, a massive coincidence, or something fundamental about information.) Languages and Automata are intimately related! For example, we can:
- Ditch the infinite tape and bound the tape to the size of the input plus one cell on either end, containing a left-end-marker-symbol on the left and a right-end-marker-symbol on the right. These cells cannot be changed nor can the TM head move off the ends. This is called a linear bounded automaton, (LBA). The languages they recognize are equivalent to those generated by a Type-1 Grammar.
- Restrict the machine to be read-only (never write anything) and only move right. This is called, and note this is a misleading name, a finite automata (FA). It is a poor name because it is not the only kind of machine with a finite number of states (all TMs have a finite number of states) and it is not the only kind with a finite memory (LBAs are bounded also). But FAs are very important: they define computations that process one symbol at a time and don’t require any scratch memory. The recognize the same class of languages as are derived by RLGs.
- Add a second tape (called the “stack”) and keep the input tape read-only and allow right-moves only. The next step is chosen based on both the current input symbol and the symbol(s) on the top of the stack, At each step you can pop symbols and push symbols. This contraption is called a pushdown automata(PDA). PDAs recognize exactly the context-free languages. PDAs can be restricted even further so that there is only one possible move to make at each step: this yields a “deterministic” PDA, known as a DPDA.
DeterminismAutomata theory is a huge topic, and there is so much more to study. We’ll get to it later. But there’s one interesting aspect worth noting now: Machines that allow more than one possible operation from a given configuration are called nondeterministic, and those that allow only one are called deterministic. Okay, fine, but here’s the philosophical question: is nondeterminism more “powerful” than determinism? That is, can we recognize more languages with nondeterministic machines of a given class than deterministic ones? It turns out:
- For FAs and TMs, there is NO difference in recognition power between deterministic and nondeterministic versions.
- For PDAs, there IS a difference in recognition power between deterministic and nondeterministic versions.
- For LBAs, we don’t know!
Who knew right? 🤯
Analytic Grammars
An analytic grammar is crafted with the idea of making recognition—going from candidate string to start symbol—much more natural. You don’t think about generating all possible utterances from the start symbol; instead, you think of matching rules to a candidate string. This idea is pretty nice when you need to write compilers or interpreters.
The biggest difference between generative and analytic grammars is in the handling of alternatives. In a generative grammar $G$, $L(G)$ is contains all strings that can be generated by applying rules whenever possible. For example, the rule $x \rightarrow y\,|\,z$ means you can replace an $x$ with an $y$ or a $z$, so you can generate both. So the grammar:
$s \longrightarrow \texttt{"a"}\;|\;\texttt{"ab"}$
describes the language $\{ a, ab\}$.
In an analytic grammar, the rules are deterministic; you don’t get to pick one or the other. So $A\,/\,B$ means: “Try to match $A$. If you can, the rule matches and you are done. Otherwise (and only otherwise), try to match $B\,$”. So:
$s \longleftarrow \texttt{"a"}\;/\;\texttt{"ab"}$
recognizes the language $\{ a \}$, but:
$s \longleftarrow \texttt{"ab"}\;/\;\texttt{"a"}$
recognizes the language $\{ a, ab \}$.
Unlike generative grammars, analytic grammars feature special lookahead operators, including the negative lookahead operator (~) and the positive lookahead operator (&). This enables the definition of non-context-free languages, despite having only one symbol on the left-hand side! Here’s an analytic grammar for the non-context-free language $\{ a^nb^nc^n \,\mid\, n \geq 0 \}$:
$ \begin{array}{lcl} \mathit{s} &\longleftarrow& \texttt{&} \; (\mathit{x}\texttt{ "c"}) \; \texttt{"a"}^+\;\mathit{y} \\ \mathit{x} &\longleftarrow& \texttt{"a"} \; \mathit{x}? \; \texttt{"b"} \\ \mathit{y} &\longleftarrow& \texttt{"b"} \; \mathit{y}? \; \texttt{"c"} \end{array} $
Formal Language Classification
Time for a little side exploration into how we can categorize languages. There are a gazillion ways to do so. Perhaps the first and certainly the most historically significant classification scheme is due to Chomsky, and is now known as the Chomsky Hierarchy:
The main language types in this hierarchy are listed below.
| Language Type | Description | Grammar | Recognizer |
|---|---|---|---|
| Finite | A language with only a finite number of strings. | $S \rightarrow w_1 | \ldots | w_n$ | Loop-free FA |
| Regular (Type 3) |
A language in which strings can be recognized by processing them one symbol at a time, without backtracking, and without using additional memory. | RLG | FA |
| Deterministic Context Free (LR) |
A language recognizable on a deterministic PDA. (Stacks are nice! Θ(1) access! Determinism is nice too! Much more efficient.) | DCFG | DPDA |
| Context Free (Type 2) |
A language recognizable on a nondeterministic PDA. (Stacks are nice! Θ(1) access! But with nondeterminism, recognition is slower.) | CFG | PDA |
| Type 1 | A language recognizable on an LBA. (Type 1 languages are often called “context-sensitive,” but that is not a very accurate name because all languages “beyond” Type 1 in the hierarchy are sensitive to context). | ENCG | LBA |
| Recursive (R) | A language in which string membership is decidable. There are no predetermined memory bounds, and no bounds on the number of steps. | ? | TM that always halts |
| Recursively Enumerable (Type 0 / RE) |
A language in which string membership is partially decidable: if a string is in the language, you can determine that for sure; if a string is not, you might not be able to determine this. | (Unrestricted) Grammar | TM |
We sometimes add:
- co-RE: A language whose complement is RE
- Finitely Describable: A language that has a finite description
Fun fact: $\textit{RE} \cap \textit{co-}RE = R$.
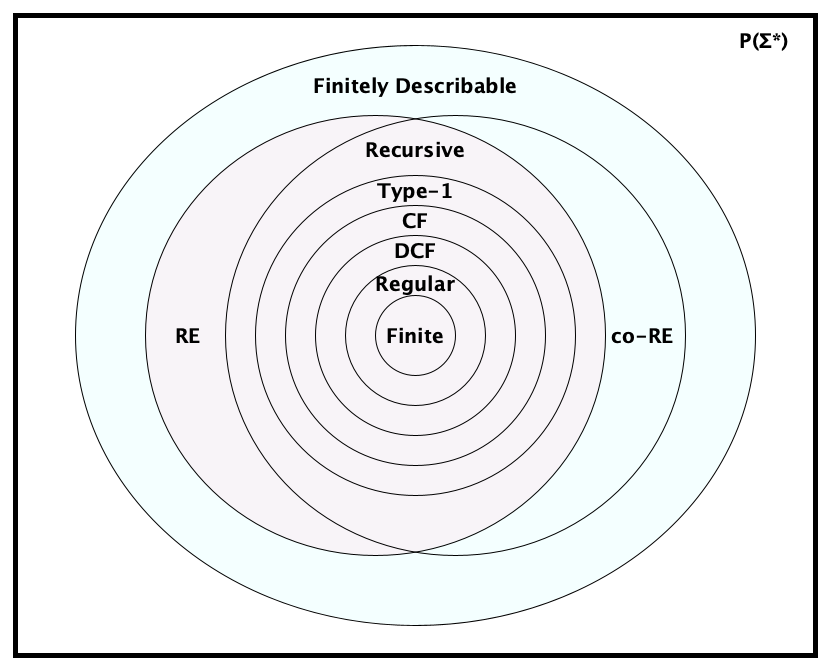
The language class RE lines up with what we understand to be computable.
The Chomsky Hierarchy is just a start. There are hundreds (no kidding) of other classes of languages. Perhaps the two most famous are:
- $\mathit{P}$: The set of all languages that can be recognized by a deterministic TM in a number of steps bounded by a fixed polynomial in the size of the input.
- $\mathit{NP}$: The set of all languages that can be recognized by a TM in a number of steps bounded by a fixed polynomial in the size of the input.
Note, by definition, $\mathit{P} \subseteq \mathit{NP}$, but no one has been able to prove whether or not $\mathit{P} = \mathit{NP}$. There is a cash prize waiting for you if you can do it.
There’s so much more, including languages tied to probabilistic and quantum computing. All of the language families described above, as well as hundreds more, can be found in the Complexity Zoo.
Semantics
Up to now, our only definition of “language” has been a set of strings over some alphabet, and we’ve looked at many ways to describe a set of strings. A description of the set of strings in the language is called a syntax. But you probably have a sense that languages exist to convey meaning. The way meaning is attached to utterances of a language is known as semantics.
For instance, we saw the language of simple arithmetic expressions above. We gave the grammar:
$\begin{array}{lcl} \mathit{exp} & \longrightarrow & \mathit{digit}^+ \\ & | & \texttt{"–"} \; \mathit{exp} \\ & | & \mathit{exp} \; (\texttt{"+" | "–" | "*" | "/" | "%" | "**"}) \; \mathit{exp} \\ & | & \texttt{"(" }\mathit{exp}\texttt{ ")"} \end{array}$
and said the language WAS the set of strings generated by this grammar. To give the utterances meaning, we could define a function mapping every utterance to its meaning, which in this case would be a number.
It’s customary to define the semantics of a language by a set of rules that show how to evaluate syntactic forms of the language. Here’s a pretty straightforward definition:
How do we deal with semantics in formal language theory? Interestingly, semantics tends to live in a different theory—not in “formal” language theory, but rather in a theory affectionately known as PLT.
Programming Language Theory (PLT)
Formal Language Theory, it seems, is only concerned with defining or determining which strings are in a language and which are not. It is not concerned with assigning meaning to those strings. We have to go beyond what we’ve learned so far to deal with questions of meaning. Linguists study semiotics. Computer Scientists study programming language theory, otherwise known as PLT.
In PLT, programming languages are, yes, fundamentally sets of strings, but where each of the members of the language is a program, representing a computation. The concern of the syntactic aspect of the formal (contrived) languages we’ve seen so far is really just to provide a foundation for studying computability and complexity, while the concern of programming languages is for humans to express powerful computations. Programming languages feature extremely rich syntaxes and complex semantics, and introduce us to two worlds: the static and the dynamic.
PLT is a significant and very active branch of computer science that deals with everything about programming languages, including their design, classification, implementation, interpretation, translation, analysis, features, expressiveness, limitations, syntax, semantics, and so on. It is concerned with:
Syntax
How do we formally specify the structure of programs?
Semantics
How do we formally specify the meaning of programs?
Type Theory
How do we classify constructs and entities in our programs (by their structure and behavior)?
Static Analysis
What can we say about a program just by looking at it (without running it)?
Translation
How do we construct compilers (translators) and interpreters (executors)?
Runtime Systems
What do programs look like at runtime, and what do we need to execute them?
Verification
How do we mechanically prove program properties, such as correctness and security?
Metapro-
gramming
How do we write programs that operate on, and generate, other programs?
Classification
On what bases can we rigorously classify PLs in meaningful ways?
Basically, anything in the study of Programming Languages seems to fall under the topic of PLT. But in the popular culture, the PLT community seems to be associated with the most theoretical, the most mathematical, the most foundational. PLT people write papers whose formulas have a lot of Greek letters. Logic and category theory are everywhere. And when it comes to actual programming, the PLT community is all over the most cutting-edge stuff, like dependent types. And they appear to favor functional programming languages. Haskell, Scheme, and the ML Family of Languages show up a lot in current research. So do proof assistants, like Agda, Coq, and Lean.
This is good, though.
PLT is a huge field but there is good news for students: Some one has already built, and is currently maintaining, a most excellent curated portal for PLT. So many great links to books, papers, articles, tutorials, and even to other portals! Browse and lose yourself in the good stuff.
You can also begin a journey at Wikipedia’s PLT article.
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- Why do we need a theory of language? A theory of language allows us to rigorously define exactly how we may express and transmit information.
- What is information and how do we conventionally represent it? Information is that which informs. Technically, it can be defined as a resolution of uncertainty. We represent it with a string of symbols.
- What is an alphabet, in language theory? A finite set of symbols.
- What is a string, in language theory? A finite sequence of symbols over a given alphabet.
- How do we denote the empty string (the string of zero symbols)? $\varepsilon$
- What is $|abbabcb|$? 7
- How do we denote the concatenation of two strings $x$ and $y$? $xy$
- What is $ho^3$? What is $(ho)^3$ $hooo$
$hohoho$ - Why is the traditional representation of concatenation and repetition so annoying? String concatentation is written like multiplication, but it is really a kind of addition. String repetition is written like exponentiation, but it is really a kind of multiplication.
- What are the substrings of $abc$? $\varepsilon$, $a$, $b$, $c$, $ab$, $bc$, $abc$.
- What is a language, in formal language theory? A set of strings over some finite alphabet.
- What do we call a member of a language? An utterance.
- What is the difference between $\varnothing$ and $\{ \varepsilon \}$? The former is the language of zero strings; the latter is a language with one string, namely the empty string.
- How do the Kleene Closure and the Positive Closure of a language differ? The Kleene Closure includes the empty string; the Positive Closure does not.
- How do we denote the concatenation of two languages, $L_1$ and $L_2$? $L_1L_2$
- What is $\{a, b, c \}^2$? The set of all strings of length 2 over the alphabet $\{a, b, c\}$, namely $\{aa, ab, ac, ba, bb, bc, ca, cb, cc\}$.
- For language $L$, what are $L\varnothing$ and $L\{\varepsilon\}$? $\varnothing$ and $L$, respectively.
- What are the two means by which we can formally, but “computationally,” define a language, other than listing all the strings or providing a description with a set comprehension? By generation or recognition.
- What is the primary mechanism for which languages are described by generation? The generative grammar.
- What are variables in a generative grammar? Symbols that are distinct from those symbols in the language that the grammar is defining, that are intended to be replaced by (strings of) symbols in the process of generating strings in the language.
- What do the metacharacters $|$, $*$, $+$, and $?$ mean in a generative grammar? Alternation (OR), repetition (Zero-or-more), positive repetition (One-or-more), and optional (Zero-or-one), respectively.
- How do we denote the language defined by grammar $G$? $L(G)$
- When taking about grammars, we sometimes see the metacharacters $\longrightarrow$ and $\Longrightarrow$. What do they mean? The former is used to denote a rule in a grammar; the latter is used to denote a derivation step.
- When does a derivation in a generative grammar “stop”? When there are no more variables.
- What is the single rule in the generative grammar defining the language of positive odd binary numerals? $odd \rightarrow (\texttt{"0"} \mid \texttt{"1"})^*\;\texttt{"1"}$
- What language is defined by the following generative grammar?
$\;\;s \longrightarrow \texttt{"a"}\;s?\;\texttt{"b"}$
$\{ a^nb^n \mid n \geq 1 \}$ - How do you write a grammar for the language of nested and balanced parentheses? $s \longrightarrow (\texttt{"("}\;s?\;\texttt{")"})^*$
- Why was writing the grammar for $\{ a^nb^nc^n \mid n \geq 0 \}$ conceptually harder than writing the grammar for $\{ a^nb^n \mid n \geq 0 \}$? Because the former requires either (1) left hand sides with multiple symbols or (2) the use of lookahead operators.
- What are some predefined variables that are often used in grammars? $digit$, $hexDigit$, $letter$, $alnum$
- For the grammar
$\;\;s \longrightarrow \texttt{"a"}\;s?\;\texttt{"b"}$
what does the derivation tree for the string $aabb$ look like?s / | \ a s b /|\ a s b | - The grammar
$\;\;s \longrightarrow x \mid y$
defines a language with exactly one utterance, namely $ab$. But there are two possible derivations. Show them.
$\;\;a \longrightarrow x$
$\;\;y \longrightarrow b$- $s \Longrightarrow xy \Longrightarrow ay \Longrightarrow ab$
- $s \Longrightarrow xy \Longrightarrow xb \Longrightarrow ab$
- What does it mean for a grammar $G$ to be ambiguous? There exists a string in $L(G)$ with more than one derivation tree for $G$.
- What are the four components of the mathematical structure representing a formal, generative grammar? The structure is $(V, \Sigma, R, S)$ where $V$ is the set of variables, $\Sigma$ is the alphabet over which the language is defined, $R$ is the set of rules, and $S$ is the start symbol.
- In a generative grammar, $(V, \Sigma, R, S)$, we require $R \subseteq (V \cup \Sigma)^*V(V \cup \Sigma)^* \times (V \cup \Sigma)^*$. Explain this requirement. Rules map over strings of variables and language symbols (that is, strings from $(V \cup \Sigma)^*$), but the left hand side MUST have at least ONE variable.
- Why does the formal definition of a grammar not include $?$, $*$, $+$, or $\mid\,$? Because when doing super theoretical meta-level work, brevity and simplicity are key. We want the smallest possible number of building blocks to simplify discussions about what grammars are. We can define these constructs in terms of the basic constructs.
- How is the derivation relation $\Longrightarrow_{\small R}$ in a generative grammar formally defined? $\{ (xwy, xzy) \mid w R z \}$
- What are alternate terms used by different authors for “variable” and language symbol”? “Nonterminal” and “terminal”
- What do we call the union of variables and language symbols? The vocabulary
- What is a context-free grammar (CFG)? A restricted form of a generative grammar in which the left hand side of every rule is a single variable.
- What is a right-linear grammar (RLG)? A restricted form of a generative grammar in which the right hand side of every rule is a string of zero or more symbols followed by at most one variable.
- What is an essentially noncontracting grammar (ENCG)? A restricted form of a generative grammar in which the right hand side of every rule never has fewer symbols and variables than the left hand side, with one exception: if the language contains the empty string, we can have one rule that maps the start symbol to the empty string.
- What are two mechanisms to recognize languages? Automata and analytic grammars.
- What is the most well-known and influential kind of automaton? The Turing Machine.
- What restrictions of Turing Machines correspond to RLGs, CFGs, and ENCGs? Finite Automata, Pushdown Automata, and Linear Bounded Automata, respectively.
- What is the difference between a deterministic and a nondeterministic automaton? Deterministic automata have only one possible transition to take when in a given configuration; nondeterministic automata have more than one.
- What is the difference between a generative and an analytic grammar? Generative grammars generate all and only the strings in a language. Analytic grammars define a process to determing whether a candidate string is in the language or not.
- What is the language defined by the analytic grammar $s \longleftarrow \texttt{"a"}\;/\;\texttt{"ab"}$? The language $\{ a \}$. (Importantly $ab$ is not in the language because when presented with that string, the grammar matches the $a$ part and will not backtrack to try the second alternative.)
- Although analytic grammars have only a single variable on the left hand side of each rule, how can they define non-context-free languages? By using lookahead operators.
- The classic arrangement of language classes in terms of computation power is known as the ________________. The Chomsky Hierarchy
- What is a finite language and what kinds of grammars generate them and what kinds of automata recognize them? A language with only a finite number of strings. They are generated by a grammar in which every rule maps the start symbol to a string in the language. They are recognized by a loop-free finite automaton.
- What is a regular language and what kinds of grammars generate them and what kinds of automata recognize them? A language in which strings can be recognized by processing them one symbol at a time, without backtracking, and without using additional memory. They are generated by a right-linear grammar. They are recognized by a finite automaton.
- What is a context-free language and what kinds of grammars generate them and what kinds of automata recognize them? A language in which strings can be recognized by processing them one symbol at a time, without backtracking, and by using only a simple stack for working memory. They are generated by a CFG. They are recognized by a PDA.
- What is a Type 1 language and what kinds of grammars generate them and what kinds of automata recognize them? A language in which strings can be recognized with fixed apriori bounds on working memory. They are generated by an ENCG. They are recognized by an LBA.
- What is the difference between a recursive and a recursively enumerable language? Recursive languages are decidable, that is, recognizable on a always-halting Turing Machine; recursively enumerable languages are partially decidable, meaning they can be recognized by a Turning Machine that always halts for YES answers but may loop forever on strings not in the language.
- Arrange R, FINITE, RE, DCFL, CFL, and REG in subset order. FINITE $\subset$ REG $\subset$ DCFL $\subset$ CFL $\subset$ R $\subset$ RE
- What is $RE \cap \textrm{co-}RE$? R
- What is a “computable language”? A language that is recursively enumerable.
- What is the language class P? The set of languages that can be recognized by a deterministic TM in polynomial time.
- What is the language class NP? The set of languages that can be recognized by a TM in polynomial time.
- What is semantics concerned with? The meaning of utterances in a language.
- What is the difference between a number and a numeral? A number is an abstract concept; a numeral is a representation of a number.
- What are some of the concerns of PLT? Try to name at least five. Syntax, Semantics, Type Theory, Static Analysis, Translation, Runtime Systems, Verification, Metaprogramming, Classification.
- Who is the curator of the GitHub portal for PLT? Steven Shaw
Summary
We’ve covered:
- Symbols, alphabets, and strings
- Formal Languages
- Grammars
- Parse Trees
- Ambiguity
- The formal definition of a grammar
- Context-Free, Right-Linear, and Type-1 Grammars
- Language Recognition
- The Chomsky Hierarchy
- A bit of history
- What Programming Language Theory is concerned with