Turing Machines

The Backstory

History helps a lot! Why do we have Turing Machines? Why do we care? Why are we better knowing about Turing Machines than not knowing them?

Hear the answers in class. We’ll go through 19th century advances in logic, the formalists versus the intuitionists, Hilbert’s Challenges, the need to formalize computation, Gödel’s and Church’s approaches, and how Turing’s view of computation was the most mechanistic (as opposed to logical or mathematical) and influenced by human computers of the day, and how he (Turing) translated all these ideas into simple mathematical constructs that in some real sense....nailed it!

The Basic Idea

Turing looked at computers of his day and asked “What are these people doing?” He thought about it and realized these folks would write something down, think for a bit, write something else or erase something, think some more, write or erase, and so on. They would move from mental state to mental state as they worked, deciding what to do next based on what mental state they were in and what was currently written.

He realized he could capture this process formally and keep the model very simple: instead of a two-dimensional page, a single one-dimensional tape would do, and instead of randomly jumping around, it would be okay to move one cell at a time. Today we picture the machines like this:

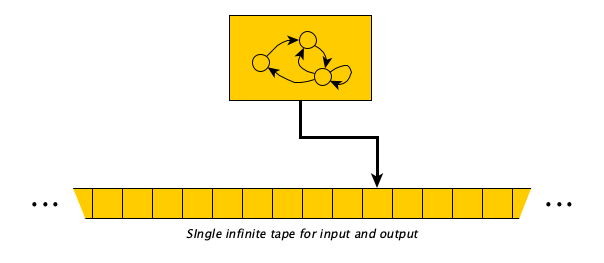
Jade’s video, again:

Thirteen Examples

Let’s see some examples before we get formal.

Formal Definition

Y’all set for a formal definition? Here is the definition for a transducing TM:

What about the recognizer flavor? It’s just this:

There is more than one kind of Turing Machine

The definition above is the one I like best.

In this definition, the transition relation was allowed to be any relation whatsoever. In fact, it is non-deterministic: at each step, the machine may have multiple choices regarding what to next! And the machine runs until it hits a configuration with nowhere to go.

We will see variations later, including deterministic models which require the transition relation to be a function, and a special $\textsf{HALT}$ state, or $\textsf{HALT}$ action, to be introduced.

Case Study

Let’s use the formal definition to describe a Turing Machine that increments a binary number. Here’s the machine as a picture:

Let’s identify the parts. Our machine is $(Q, \Sigma, \Gamma, \#, \textsf{R}, \textsf{G})$ where:

We can condense this a bit, using only the rule set, making sure the start symbol appears first (spaces added for clarity):

    G00RG G11RG G##LF F01LH F#1LH

You can come up with a canonical encoding, where states are 0, 1, 2, ...; $\Sigma$ is $\{ 0,1 \}$; the symbols in $\Gamma - \Sigma$ are 2, 3, 4, ... with the blank being 2; Left is 0 and Right is 1:

    00010 01110 02201 10102 12102

More Examples

If the 13 examples in the video were not enough, we have more.

Binary Decrement

TODO

Reverse a String

TODO

Binary Addition

TODO

Parity

TODO

Is Divisible by 5?

Take the empty string to be 0. Read the binary string from left to right. Whenever you see a zero, your current number goes from $n$ to $2n$. Whenever your see a 1, your number increases to $2n+1$. Keep track of the current number modulo 5. You accept if you finish with a number whose value mod 5 is 0.

Even More Examples

Want even more examples? Check out this article with six interesting examples, including:

• Binary addition
• Converting binary to unary
• Converting unary to binary
• Doubling the length of a sequence
• The 4-state busy beaver
• Palindrome detection

Variations on the Turing Machine

Let’s mix things up a bit.

Determinism

We’ve defined our machines with a transition relation that could have multiple outgoing transitions from a state for the same configuration. But what if we required the machine to have, for every state, one and only one transition? That is, instead of:

$$ R \subseteq (Q \times \Gamma) \times (\Gamma \times \{L, R\} \times Q) $$

we required $R$ to be a function? Doing so would require us to expand the codomain of the function so that the machine could stop. We could add a halting action:

$$ R : (Q \times \Gamma) \rightarrow (\Gamma \times \{L, R\} \times Q) \cup \{ \textsf{HALT} \} $$

This says: if the machine is in some state $\sigma \in Q$, and currently looking at a symbol $\sigma \in \Gamma$, then either:

1. Replace the symbol with a new symbol $\sigma'$, move one cell, and enter state $q' \in Q$, OR
2. Halt

A slightly different definition of a deterministic Turing Machine treats “halting” as a kind of state, a halting pseudo-state:

$$ R : (Q \times \Gamma) \rightarrow (\Gamma \times \{L, R\} \times (Q\cup \{ \textsf{HALT})) \} $$

This says: if the machine is in some state $\sigma \in Q$, and currently looking at a symbol $\sigma \in \Gamma$, then:

1. Replace the symbol with a new symbol $\sigma'$, move one cell, THEN
2. Either enter state $q' \in Q$ or Halt

How many $n$-state deterministic TMs are there?

Recall from your discrete math class that the number of functions over finite domain $D$ and finite range $R$ is $|R|^{|D|}$ — you did pay attention in that class, right? Haha, it’s okay, I had forgotten that too.

We will show that, for the halting-pseudo-state version, the domain has size $2n$ and the range has size $4(n+1)$.

Hint

Domain: $n$ states and 2 symbols; Range: 2 symbols we can write, 2 directions we can move, and $n+1$ places to “go.”

Later we will see why this is interesting.

The definition is a little clunkier, but it’s kind of nice. Interestingly, this simplification does not change the computing power of the model.

Stationary “Moves”

Instead of having to go left or right at each step, you can also provide to option to stay put. No change to computing power.

$$R \subseteq (Q \times \Gamma) \times (\Gamma \times \{\textsf{L},\textsf{R},\textsf{X}\} \times Q)$$

Here X means stay on the same cell.

$\varepsilon$-Moves

In the base model, the machine looks at the current symbol and decides what to do next. We can let it just decide to jump to another state without examining the current symbol. Again, no change in computing power.

$$R \subseteq (Q \times (\Gamma \cup \{ \varepsilon \})) \times (\Gamma \times \{\textsf{L},\textsf{R}\} \times Q)$$

Multidimensional Tapes

How about, instead of a tape that is infinite only in the left and right directions, we make a two dimensional tape that can go up and down also? Or a 3-D tape? Or make a machine whose tape is any finite number of dimensions? All good. These extensions do not increase the computing power of the model.

One-way Infinite Tape

What if the tape had a left-end, and was infinite only to the right? A little messier to program, perhaps, but no change in computing power.

Multiple Tapes

More than one tape? More convenient. But you guessed it, no change in computing power.

Stack and Queue Tapes

If we restricted our tape memory to act like a queue, we have a Queue Automaton and no change in computing power. But if our tape was stack-like, we’ve reduced our power: we can no longer compute certain functions (recognize certain languages). But if we had two stacks we are back to full power.

Read-Only and Write-Only and Append-Only Tapes

Sometimes we might want to have a bunch of tapes and use certain tapes only in certain ways. Maybe we can only read or only write or only append. Hmmm, tapes are starting to look flexible. We can imagine a tape that is:

• Unbounded on both ends, bounded on one end and unbounded on the other, bounded on both ends
• 1-dimensional, 2-dimensional, ... $n$-dimensional
• Read-only, Write-only, Append-only
• Stack-like, Queue-like, Move one cell at a time, Take big jumps
• One way (say right-moves only or left moves only) or multi-way

Linear Bounded Automata (LBAs)

What if we bounded the tape on both ends? There’s this thing called a Linear Bounded Automaton which is a TM with a bounded tape, just big enough to hold the input and two additional special tape symbols, the left-end-marker and the right-end-marker. These symbols can not be overwritten, and you cannot move beyond them. They are super convenient because how else would keep from falling off the ends?

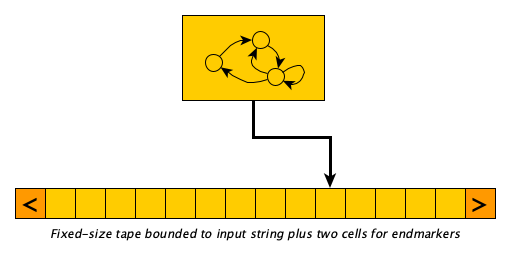
Any change in computing power? It turns out yes. The computing power is reduced.

Pushdown Automata (PDAs)

It turns out that the class of context-free languages can be decided exactly by a machine with two tapes: (1) a bounded, read-only, right-move only table holding exactly the input, and (2) a stack-like, one-way infinite tape for whatever you need. This kind of machine is called a push-down automaton (PDA). It is useful because stacks are super efficient, $\Theta(1)$ for pushing and popping. The PDA runs until there is no transition to make, or until the machine exhausts its input.

If you want a PDA transducer, add an output tape.

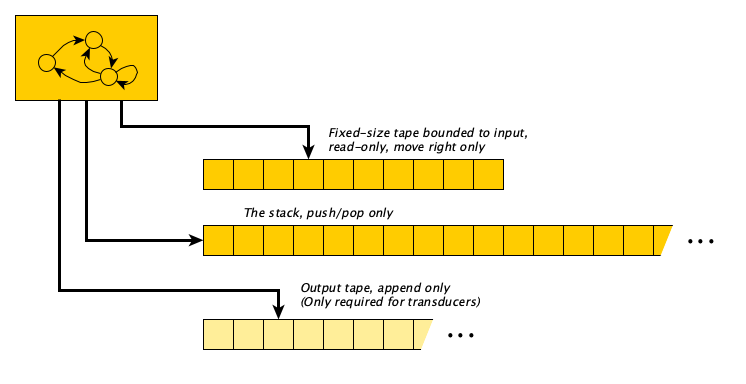
Finite Automata (FAs)

What if we had no memory at all? We’d have something called a Finite Automaton.

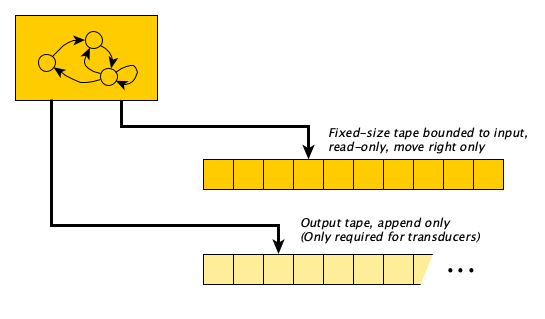
A lot of computations fall into this category.

An Online Simulator

When writing a Turing machine to carry out a computation or decide a question, don’t just guess! Use a real online simulator to check your work!

The Universal Machine

The most brilliant idea ever.

OMG.

Check this out. Remember that Turing Machine we saw above to increment a binary number? Remember how it could be encoded as a string:

0001001110022011010212102

Every Turing Machine can be represented as a string. Turing Machines take strings as input. Wouldn’t it be cool if we could make a single TM that could read the description of a machine $M$, along with some other input $w$, and simulate $M$ running on $w$?

Turing showed this was possible.

A machine that that do this is called a Universal Turing Machine.

The existence of a UTM shows that general purpose computers are possible. Indeed Turing’s work predated real general purpose computers.

To see how Turing found the Universal Machine, start at Wikipedia.

Busy Beavers

An $n$-state busy beaver is a deterministic $n$-state, halting, Turing Machine with $\Sigma = \{ 1 \}$ and $\Gamma = \{b, 1\}$ that writes the largest number of 1s on an initially blank tape over the set of all such $n$-state, halting Turing Machines, using the second definition of deterministic Turing Machine above (the kind that is allowed to write a symbol before halting).

Why on Earth would be care about such things? Let’s find out. First, let’s see what we are up against. Previously we saw that the number of deterministic $n$-state Turing Machines is $(4(n+1))^{2n}$. Hey that’s a lot of Turing Machines! For fun, here are the first few values:

$n$	$(4(n+1))^{2n}$
0	1
1	64
2	20736
3	16777216
4	25600000000
5	63403380965376
6	232218265089212416
7	1180591620717411303424
8	7958661109946400884391936
9	68719476736000000000000000000

For a given $n$, some of these machines will halt, and some will not. Now we can go through all the halting ones (haha) and count the number of 1s they print out. The maximum number we find is $\Sigma(n)$. Let’s see what these values are:

$n$	$\Sigma(n)$
0	0
1	1
2	4
3	6
4	13
5	at least 4098
6	greater than $3.515 \times 10^{18267}$
7	greater than $10^{10^{10^{10^{18705353}}}}$

Woah.

It seems amazing that we know what $\Sigma(4)$ even is! Knowing this means that for each of the 25.6 BILLION 4-state, 2-symbol Turing Machines, someone figured out whether it halts or not, and if it halts, what it outputs. Finding $\Sigma(5)$ will be harder: there are over 63.4 TRILLION machines to investigate.

That’s a lot of machines to go through. And it’s not easy to figure out whether a long-running machine will eventually halt or not. Such a machine might take years or centuries to finish, so we can’t just run it and see. We have to painstakingly analyze each machine, and we have to sometimes be really clever. And if we know a long running machine will halt, we need a clever way to figure out how many 1s it will output, because this number might be too big to actually store. Can you see now why people that try to find these values are called Busy Beaver Hunters?

Here is a 3-state Busy Beaver you can try out:

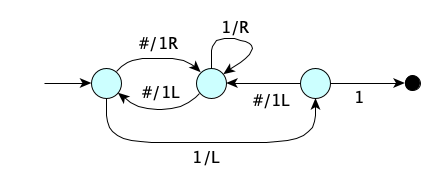
You can read more about Busy Beavers at OIS and at Wikipedia.

More Busy Beaver Fun To Follow

When we study computability theory, we’ll see that $\Sigma$ is not a computable function. Although it has a well-defined finite description, no computing device can compute it. In fact, it grows faster than any computable function.

Imagine that.

Impatient? Here is a very nice short paper with formal proofs that $\Sigma$, and its friend $S$ (function for the maximum number of steps a 2-symbol, $n$-state DTM takes), are uncomputable.

Here’s more on Busy Beavers:

Summary