Automata Theory
Motivation and History
The field we now call automata theory arose from many different areas of research, including:
- Mathematics, through attempts to formalize the meaning of computation
- Engineering, through attempts to characterize (discrete) physical systems
- Psychology, through attempts to characterize human thinking and reasoning
These folks all came up with the notion of an automaton as a kind of machine, real or abstract, that follows a fixed set of instructions to carry out a step-by-step procedure.
A brief history of the field can be found at Wikipedia.
We want a rigorous theory of automata. Therefore, we will make the following assumptions about the automata that we study:
- A machine must have a finite description.
- The input to the machine is represented as finite string of symbols that come from a fixed alphabet.
The first assumption is reasonable because a machine that requires an infinite description could not be built, let alone understood. The second is motivated by the fact that it’s pretty difficult (impossible?) to conceive of any kind of information that we could not represent with strings of symbols. For example, the following capture quite a variety of information:
91772.3e-8Stay behind the yellow line!ᐊᐃᖓᐃ ᓄᓇᕐᔪᐊᖅ/Pecs/Los Angeles/Berlin/Madrid//1 2/3 0/2 2/2 0/3 2///(* (+ 4 3) (- 9 7))int average(int x, int y) {return (x + y) / 2;}<dog id="30024"><name>Lisichka</name><age>13</age></dog>{"type": "dog", "id": "30024", "name": "Lisichka", "age": 13}∀α β. α⊥β ⇔ (α•β = 0)1. f3 e5 2. g4 ♛h4++
Why create and study a theory of automata? Two reasons:
- It gives us a framework in which we can ask what computation is, what we can compute, what is necessary for computation, and how computations can be carried out.
- It provides insights into how we can design and build both real and abstract machines—and even programming languages! Abstract machines are quite important because they show how to carry out computations independent of any real machine and independent of any real high-level programming language, allowing us build multi-language compiler systems (where the abstract machine serves as a conceptual representation of a program):
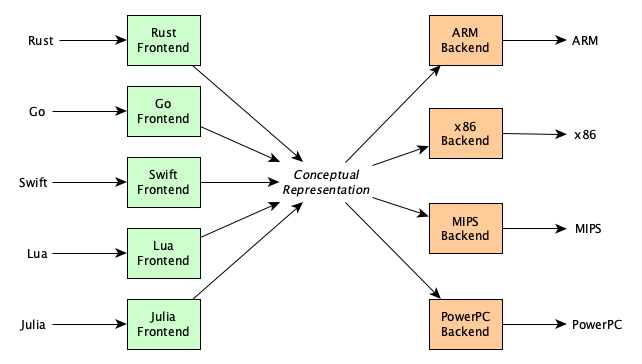
Kinds of Automata
An automaton is any device, physical or abstract, that runs by itself (hence the prefix “auto”) to process some information. There should be no limits to your imagination regarding how an automaton should or should not look, nor what kinds of internal operations it carries out (as long as it is finitely describable).
People have created many kinds of automata. Some strive to be as minimal as possible (theoretically valuable, but hard to work with in practice); some are much more complex internally (but easier for humans to work with). In terms of technical details, there are at least four dimensions on which we can characterize automata:
- (Behavior) Is the machine just answering a YES/NO question or computing a result?
- (Operation) How does the machine represent and execute each step of a computation?
- (Memory) Where are the inputs, outputs, and scratch data stored?
- (Architecture) Is the program hard-wired into the machine, or stored in memory with data?
There are more dimensions: synchronous vs. asynchronous, deterministic vs. non-deterministic, definite vs. probabilistic, classical vs. quantum, etc. But as these notes are introductory, we will focus only on the first four dimensions.
Behavioral Variations
Our first dimension is one of convenience only.
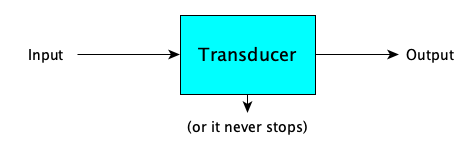
- A transducer automaton transforms an input into an output (if it finishes):
- A recognizer automaton accepts or rejects its input, by answering a YES-NO question about the input (if it finishes):
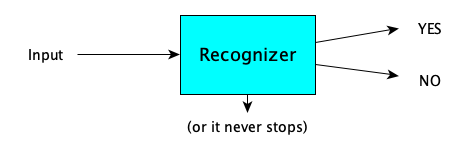
If a recognizer machine $M$ says YES to input $w$, we say that $M$ accepts $w$.
A recognizer that always finishes and answers YES or NO (and never loops) is called a decider.
Operational Variations
There are variations on how the automata are structured, particularly how their control unit, or algorithm, is specified. The main options are with a (1) a state machine, (2) a set of instructions, or (3) a set of rewrite rules.
- A state machine automaton performs a computation by moving through states that indicate in which phase of the computation one is in. The “program” is basically a transition table. The computation ends when you land in a state that doesn’t have a transition out of the current state for the current machine configuration. Transition tables come in many forms, depending on the type of state machine, but are generally structured like so:
If you are in
this stateand this
event occursThen perform
this actionand move
to stateState machines can also be given with pictures:
If there can be more than one action/transition to take from a given state/input configuration, the machine is said to be non-deterministic, otherwise it is deterministic.
- An instruction-set machine has a control made up of a list of instructions. Normally instructions are executed in order, but some machine operands can be references to other instructions (e.g., via labels or by position) to allow conditional and iterative execution. Instructions that directly reference other instructions to explicity change the control flow are called branches or jumps. Details coming soon.
┌───────────────────┐ │ Instruction 0 │ ├───────────────────┤ │ Instruction 1 │ ├───────────────────┤ │ Instruction 2 │ ├───────────────────┤ │ . │ │ . │ │ . │ ├───────────────────┤ │ Instruction n-1 │ └───────────────────┘
- A rewrite machine is an automaton specified with a set of rewrite rules that transform the input to the output. For recognizers, we can have the output be a designated
YES or NO symbol. The “program” defined by a rewrite system is something like:If you see this substring Rewrite with this substring Exercise: Imagine non-deterministic vs. deterministic string rewriting machines. What issues come up in distinguishing these variations?
Are these really all the same in some sense? Are these distinctions just for human convenience?
Memory Variations
There’s a lot of variety in memory, but two primary kinds are:
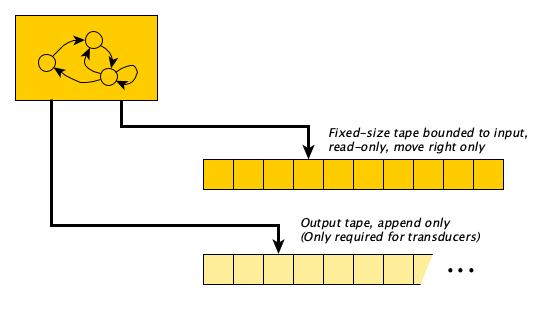
- Tapes: a tape is sequence of cells, each holding a single symbol. At any point the machine is looking at a current cell on the tape. The machine can move left or right only. The tape can have a finite number of cells, or can be infinite in one direction, or infinite in both directions. A machine can have multiple tapes. There are models where tapes are restricted to be read-only, write-only, stack-like (push/pop only), or queue-like (enqueue/dequeue only).
─┬───┬───┬───┬───┬───┬───┬───┬───┬───┬─ • • • │ │ | | | | | | | | • • • ─┴───┴───┴───┴───┴───┴───┴───┴───┴───┴─ - Registers: A machine can have one or more registers. Each register holds some data. Usually in automata theory, a register holds a natural number (nonnegative integer) of unbounded size, but variations allow it to hold only a single symbol, or maybe a floating-point (but not real) number, or even a string. Registers are numbered $r_0, r_1, r_2, \ldots$ and they can be accessed by their number. Some models have a finite number of registers; in others, infinite. There can even be different classes of registers: for example, maybe only certain registers can do arithmetic, maybe only certain registers can be used for indirect addressing, etc.
┌────────────────────┐ r0 │ │ ├────────────────────┤ r1 │ │ ├────────────────────┤ r2 │ │ ├────────────────────┤ r3 │ │ ├────────────────────┤ r4 │ │ ├────────────────────┤
What else? You can have fun, too, with things like multi-dimensional tapes. (A two-dimensional tape would allow for up, down, left, and right movements.) Use your imagination to build new computing machines.
Architectural Variations
One final variation of interest, applicable to instruction-based automata only, really, is: where are the instructions stored? There are two main architectures:
- Harvard Architecture: Instructions are stored in a dedicated, read-only instruction unit, separate from data.
- Von Neumann Architecture: Instructions are stored together with the data.
Classic Examples of Automata
Turing Machines (TMs)
Turing Machines are so historically significant and influential, that I have an entire separate page of notes on them.
But the basic idea is that the input sits on a infinite tape of cells surrounded by blanks. The machine has a head pointing to the first symbol of the input. The machine’s control is a finite set of rules that says “If in state $q$ looking at symbol $\sigma$, then maybe replace the current symbol with $\sigma'$, maybe move either one cell right or left, and then maybe transition to state $q'$.”
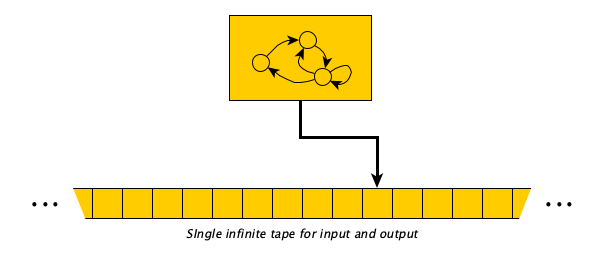
We’ll cover Turing Machines in detail later, but for now here’s an example Turing Machine (of the transducer variety) to increment a binary number:
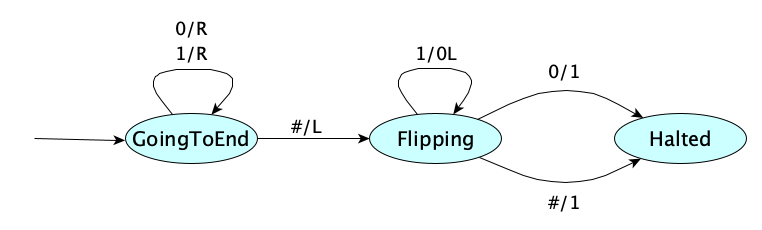
A variation on the Turing Machine, one that does not change its power in anyway, is to make each action be comprised of a mandatory print and a mandatory move. In that variation, our state diagrams are usually written like so:

Get used to multiple variations and notationsIt turns out there are way more than two variations of the Turing Machine, and the notations can vary quite a bit. They all have in common that “when in state $q$ looking at $\sigma$, perform actions (maybe) and transition to a new state (maybe)”. The variations have to do with how many actions (writes, erases, and moves) you may perform.
These notes will use both transition notations (e.g.,
0/Rand00R), so get used to reading both. There is no right or wrong way.
Watch Jade’s video again:
Roleplay, with paper and pencil, the human computer of Turing’s day sitting at a desk carrying out the task of incrementing the binary number 11010011111. Put yourself in each “mental state” expressed in the above machine.
And here is one (of the recognizer) variety to determine if a given unsigned binary number is divisible by 3:
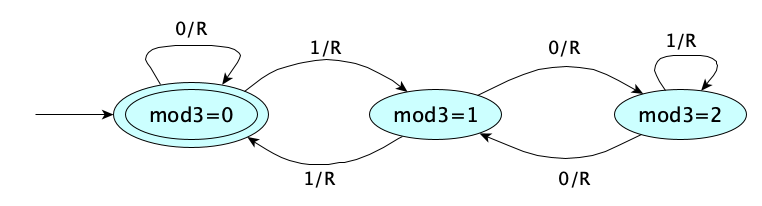
Later, we’ll talk about how we came up with these beauties. Not too bad for us, right? But how the heck did Turing just figure all this stuff out to begin with? Pretty amazing, right? Yes, it is amazing even though his work was massively influenced by previous work of Gödel and Church and others, which Turing was happy to acknowledge.
Wait, only one tape?
Can a Turing Machine have multiple tapes? Sure. Turing was going for simplicity (if not outright minimalism) when we introduced this machine as a model for computation. You can show that any TM with multiple tapes can be simulated with a 1-tape TM, so various other tape-based models of computation can generally be considered kinds of Turing Machines. Some of these we’ll see right now.
Linear Bounded Automata (LBAs)
An LBA is a Turing Machine whose tape is not infinite but rather contains only its input with one cell to the left containing an non-replaceable “left-end-marker symbol” and one cell to the right containing a non-replaceable “right-end-marker” symbol.
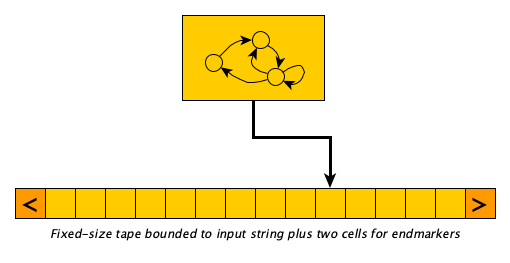
It feels a little more realistic, closer to a real computer, because of it having a finite “memory,” right?
Pushdown Automata (PDAs)
A PDA is an automata with a finite-state control, with a read-only input, and separate stack. At each step you read the next input symbol, and depending on the current top of the stack and the current state, you pop from the stack, push something new, and move to a new state.
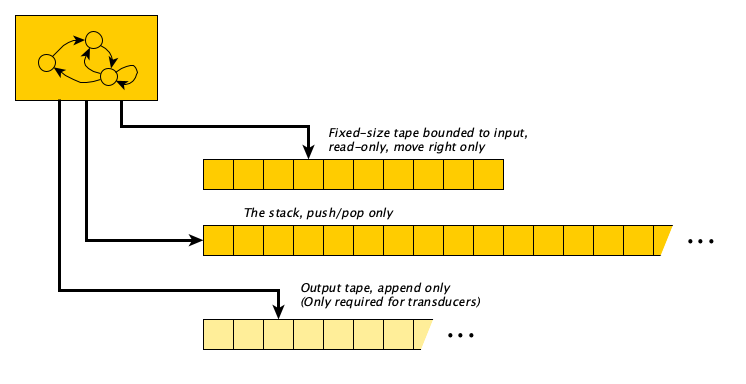
Type-3, or “Finite” Automata (FAs)
A Type-3 Automaton, often called just a Finite Automaton or FA, is a Turing Machine whose input is read-only and that only moves to the right on each step. For transducing FAs, the output is written to a separate output tape that is write-only, initially blank, and only appended to.
Do not let this terrible name confuse youIt is unfortunate that these machines are called finite automata, because Turing Machines have a finite number of states, as do LBAs and PDAs. Maybe it is because of finite memory? No. LBAs have finite memory. No one has a good name for this class of automata. Everyone calls them FAs.
Perhaps if you never heard of LBAs the name might make sense.
By the way, you may sometimes hear them called FSMs for “finite state machines” but that is much, much worse since all reasonable automata have a finite number of states and the acronym is easily confused with the deity of Pastafarianism.
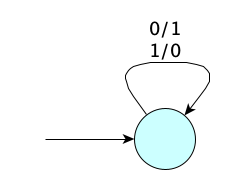
When describing FAs, we don’t have to worry about blanks, or say whether we are moving left or right! All we need is the input symbol and the output symbol(s). For a first example, here is a transducer FA that computes the one’s complement of its input:
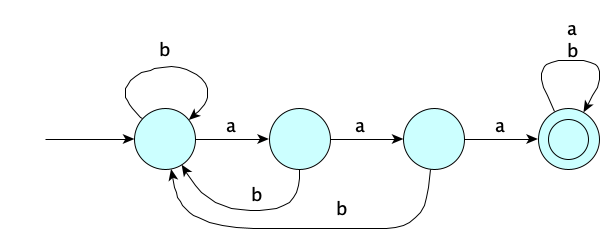
For acceptors, we don’t have any output at all, so the machine transitions just have the input symbol. Here’s an FA to determine whether its input has three consecutive $a$’s somewhere:
An FA that writes to its output on a transition is called a Mealy Machine. You can also make an FA transducer that outputs a symbol whenever it enters a state; this would be called a Moore Machine.
Queue Automata
A queue automaton is a TM that, instead of moving left or right at each step, instead always dequeues the symbol at the left and enqueues some other string of symbols on the right.
$\mathcal{P''}$
An interpreter for the $\mathcal{P''}$ language can be considered an automata. This is an exceedingly low-level and minimal notation. Check it out at Wikipedia.
Brainfuck
Like $\mathcal{P''}$, Brainfuck (or Brainf**k as it is commonly known) is a programming language with an explicit machine execution model. It is much more widely known and way easier to understand than $\mathcal{P''}$, as it is less minimal.
The execution model features (1) a fixed program stored on a read-only tape where each cell holds one of eight instructions, (2) a read-only input stream of bytes (you can think of it as a tape), (3) a write-only output stream of bytes (also a tape), and (4) a data tape with a fixed left end and infinite to the right (although really the language specification says at least 30,000 cells). The eight instructions are:
| Instruction | Description |
|---|---|
+ | Increment the byte in the current data cell |
- | Decrement the byte in the current data cell |
. | Output the byte in the current data cell |
, | Read next byte from input and store in current data cell |
< | Move left on tape |
> | Move right on tape |
[ | If byte in current data cell is 0, jump to instruction right after the next matching ] |
] | If byte in current data cell is not 0, jump to instruction right after the previous matching [ |
Here’s a program in the language. Can you figure out what it does?
+++++++[>+++++[>++>+++<<-]<-]>>++.>.
Need a hint?
7 5 2 3
7 0 10 15
0 0 70 105
72 105
See the Language overview at Esolang, the Wikipedia article, and this collection of example programs.
String Rewriting Systems
We can mechanically compute by applying rules (from a finite set of rules) that allow us to rewrite part of a string into another. We start with the input surrounded by begin and end markers [ and ], and keep rewriting, non-deterministically, there are no more rules to apply.
For example, here’s an SRS for incrementing binary numbers:
Some example runs:
- $[0] \Rightarrow [Y1 \Rightarrow 1$
- $[1] \Rightarrow [X0 \Rightarrow 10$
- $[101] \Rightarrow [10X0 \Rightarrow [1Y10 \Rightarrow [Y110 \Rightarrow 110$
- $[110010] \Rightarrow [11001Y1 \Rightarrow [1100Y11 \Rightarrow [110Y011 \Rightarrow \cdots \Rightarrow [Y110011 \Rightarrow 110011$
- $[111] \Rightarrow [11X0 \Rightarrow [1X00 \Rightarrow [X000 \Rightarrow 1000$
- $[]$ cannot be reduced, it’s an illegal input with an illegal output
How about a formal definition?
An SRS is a tuple $(\Sigma, R)$ where:
- $\Sigma$ is the alphabet of symbols
- $R \subseteq \Sigma^* \times \Sigma^*$ is the rewriting relation.
The one-step derivation relation $\Rightarrow_R \;\subseteq \Sigma^* \times \Sigma^*$ is defined as: $xuy \Rightarrow_R xvy$ iff $u R v$.
SRS Computation
An SRS $(\Sigma, R)$ computes output $w'$ from input $w$ iff $$[w] \Longrightarrow^*_R w' \wedge \forall\,x\,y\,z . w' = xyz \supset \not \exists u . (y,u) \in R$$
We can make a SRS be a recognizer, too. Here is an SRS that determines whether or not its input is in the form $a^nb^nc^n$, for $n \geq 0$:
SRS Acceptance
An SRS $(\Sigma, R)$ accepts $w$ iff $[w] \Longrightarrow^*_R \fbox{YES}$
Register Machines
Now let’s move from tapes to registers.
A register machine has a number of registers $r_0, r_1, r_2, \ldots$, each holding a single (unbounded) natural number. The machine’s control is a program, defined as a list of (labeled) instructions. The instructions are normally executed in sequence, but some instructions can cause a “jump” to an arbitrary instruction. The instruction set varies from model to model (of which there exist an infinite number of possibilities). Here’s an example of a register machine with a very small instruction set:
| Instruction | Description |
|---|---|
| $\textsf{load } r_k, n$ | $r_k := n$ |
| $\textsf{copy }r_i, r_j$ | copy contents of $r_j$ into $r_i$ |
| $\textsf{add } r_i, r_j, r_k$ | Store sum of contents of $r_j$ and $r_k$ into $r_i$ |
| ... and so on for $\textsf{sub}$, $\textsf{mul}$, $\textsf{div}$, $\textsf{pow}$, $\textsf{and}$, $\textsf{or}$, $\textsf{lt}$, $\textsf{le}$, $\textsf{eq}$, $\textsf{ne}$, $\textsf{ge}$, $\textsf{gt}$, $\textsf{shl}$, $\textsf{shr}$ | |
| $\textsf{neg } r_i, r_j$ | Store negation of the contents of $r_j$ into $r_i$ |
| $\textsf{not } r_i, r_j$ | Store bitwise negation of the contents of $r_j$ into $r_i$ |
| $\textsf{jump } n$ | Jump ahead (or back, if $n$ is negative) $n$ instructions |
| $\textsf{jz } r_i, n$ | Jump ahead (or back, if $n$ is negative) $n$ instructions if contents of $r_i$ is $0$ |
Register machines are rather important, as they are pretty much the basis for most “real” machines today. We’ll discuss them in more detail later, where we will connect them with modern machines with large and powerful instruction sets.
Lambda Calculus Interpreters
Any lambda calculus function is essentially a program. We tend to think of the $\lambda$-calculus as a formalism for modeling computation (and computable functions) in general, but one could, in theory, build hardware to carry out the operations of the calculus, so it’s fun to consider it along with more classical automata.
An early one was the SECD Machine.
μ-Recursive Functions
The μ-Recursive Functions, also known as the General Recursive Functions, or the Partial Recursive Functions, are those functions defined by a small number of rules. They allow computations in “bigger steps” than the λ-Calculus.
And More!
Yes, people have created probabilistic automata and quantum automata, too.
Connections To Formal Languages
A recognizer automata actually defines a formal language! That is, the language of machine $M$ is:
$$ L(M) = \{ w \mid M \textrm{ accepts } w \} $$Nice! This means a formal language can be defined by a grammar or by a machine. This is philosophically interesting, if not profound. It feels like there is a kind of symmetry going here.
How about an example, to understand the important concepts here, and to get the vocabulary right? Let $M$ be the Turing Machine given by the following state diagram:
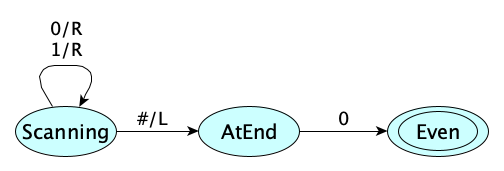
When run on any non-blank input of binary digits, the machine will end in the accept state iff the input ends with a 0. Otherwise it will get stuck. Therefore we say:
- $M$ accepts the string $110100100$
- $M$ recognizes the language $\{ w \in \{0,1\}^* \mid w \textrm{ is an even binary integer} \}$
- $M$ accepts the language $\{ w \in \{0,1\}^* \mid w \textrm{ is an even binary integer} \}$
- $M$ decides the language $\{ w \in \{0,1\}^* \mid w \textrm{ is an even binary integer} \}$
- $L(M) = \{ w \in \{0,1\}^* \mid w \textrm{ is an even binary integer} \}$
Accepting vs. DecidingIn tne example above, the machine $M$ did indeed both accept and decide the language of even binary integers. However, there do exist languages that are recognizable by a TM but not decidable by any TM. The difference between accepting and deciding is part of computation theory, and we’ll study this later.
Connections To Computability Theory
We can characterize different automata by the classes of functions they can compute, or equivalently, the languages they can recognize. For example Turing Machines can recognize a much larger class of languages than can Type-3 Machines.
So we can rank automata in increasing “power.” In the following table, the class of languages/problems in each row is a proper subset of the following row:
| Automata | Problems that can be solved / Languages that can recognized | Example |
|---|---|---|
| Loop-free FA | Finite Languages. Languages with a finite number of strings, you can basically just list them all out. Here the FA is simply a directed-acyclic graph. | $\{a,b\}$ |
| FA (Type-3 Machine) | Regular Languages. You can recognize these without any external memory whatsoever. And you can process them in linear time. | $a^*$ |
| Deterministic PDA (DPDA) | Deterministic Context-Free Languages. An interesting subset of the context-free languages. | $a^nb^n$ |
| Nondeterministic PDA (NPDA) | Context-Free Languages. It’s quite interesting, and not really too hard to prove, that the NPDAs recognize exactly the class of CFLs, which are the languages generated by a Context-Free (Type-2) Chomsky Grammar. This is a fairly natural class of languages. | $ww^R$ |
| LBA | Type-1 Languages. Bounding the tape of a TM reduces the computing power significantly! | $a^nb^nc^n$ |
| TM that always halts | Decidable Languages. Also known as the Recursive Languages, R. | $LBA_{diag}$ |
| TM | Type-0 Languages. Recursively Enumerable Languages, RE. For languages that are in RE but not in R, a TM can be found that will accept (say YES) every string in the language, but will not be able to halt and say NO for all strings not in the language. | $H$ |
| — | Finitely Describable Languages. Any language that can be finitely described, whether it can be computationally recognized or not. | $\overline{H}$ |
Can any automata compute a larger class of functions than a Turing Machine? We don’t think so. In fact, the following are all equal in computing power:
- Turing Machines
- Deterministic TMs
- One-way infinite tape TMs
- Multi-tape TMs
- Multi-dimensional TMs (e.g., can move N, E, S, W)
- Queue Automata
- NPDAs with two stacks
- Register Machines
- RAMs
- RASPs
- The μ-recursive functions
- Post Systems
- Phrase-Structure (Type-0) Grammars
- The Lambda Calculus
The fact that these all are essentially the same thing, and all attempts at making them more powerful don’t actually increase their power, led to the Church-Turing Thesis, namely, “The Turing Machine captures exactly we intuitively think of as computable.”
Applications
One of the reasons we have theories is to apply them. (Remember, a theory is an organized body of knowledge with explanatory and predictive powers.) What are some applications of automata?
Type-3 machines are used in Lexical Analysis, (extracting “words” from a string of characters), an important operation in text processing, and especially in compiler writing.
Type-2 machines are used in Parsing, uncovering the structure of a string of symbols, another hugely important and common operation.
We can see the relationship between automata and functions, through pictures like:
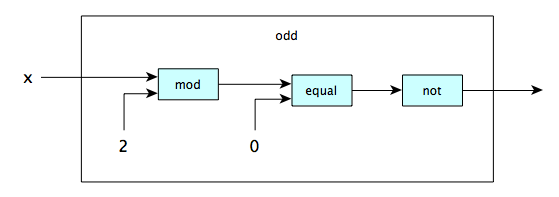
and this one:
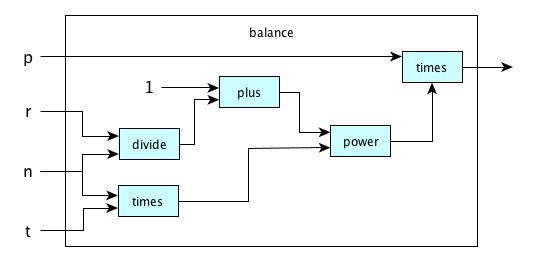
These pictures are good for humans to build a conceptual understanding of programming by combining functions.
Where to Lean More
Check out the following sources for more information:
- Wikipedia article on Automata Theory
- A Short Introduction by some folks at Stanford in 2004
- The Sipser Theory of Computation Book
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- Automata Theory evolved form multiple fields of study. Name three. Mathematics, Engineering, and Psychology.
- What reasonable restrictions do we place on automata in Automata Theory? The machine must have a finite description, and the input must be a finite string of symbols from a fixed alphabet.
- What are two useful benefits from studying automata theory? It gives us a framework to study the nature of computation and gives us insights into building real machines.
- What are four dimensions on which we can vary the design of an abstract computing machine? Behavior, operation, memory, and architecture.
- What are the two different behavioral variations of automata? Recognizers and transducers.
- What is the difference between a recognizer and a transducer? A recognizer outputs a YES or NO (or loops forever), while a transducer outputs a string (or loops forever).
- What do we call a recognizer that always stops, without looping forever? A decider.
- What are the three major operational variations of automata? Instruction-set machines, rewrite machines, and state machines.
- What is a state machine? A machine that performs a computation by moving through states that indicate in which phase of the computation one is in.
- What is an instruction set machine? A machine that performs a computation by executing a list of instructions.
- What is a rewrite machine? A machine that performs a computation by applying a set of rewrite rules to a string.
- What are the two main ways to organize memory in automata theory? Tapes and registers.
- What are the two main architectural variations of automata? Harvard Architecture and Von Neumann Architecture.
- What is the difference between the Harvard and von Neumann architectures? In the Harvard Architecture, instructions are stored separately from data, while in the von Neumann Architecture, instructions are stored together with data.
More to follow.
Summary
We’ve covered:
- What automata theory is
- Some history of automata theory
- Various types of automata
- Relationship of automata theory with formal language theory
- Relationship of automata theory to computability theory