Types
Intuition
Our very intuition makes the concept of types inescapable.
We have an intuition that integers are different from strings which are different from people which are different from books which are different from planets which are, you get the idea. These differences arise from behavior: You can open a socket, but not an integer; you can request the parents of a person, but not a dictionary; you can push an object onto a stack, but not onto character. Intuitively:
A value’s type constrains the way it may be used in a program.
More philosophically:
Types impose constraints on what we can and cannot say.
But actually, types are not only useful, they are actually one of the most fundamental concepts of all, able to serve as the foundation for all of mathematics. It makes sense to begin the study of all things with types. Ask yourself: where do things even come from?
Where Things Come From
Here is a way to bring things into existence. We start with the concept of a type, then define (exhaustive) rules that create things to inhabit the types. Here is our first type:
$$ \dfrac{}{\textsf{true}\!: \textsf{Bool}} \quad\quad\quad \dfrac{}{\textsf{false}\!: \textsf{Bool}} $$That is, the type $\textsf{Bool}$ is inhabited by exactly two values, $\textsf{true}$ and $\textsf{false}$. No more, no less. We have created two things. And a type.
Now here is the type of natural numbers:
$$ \dfrac{}{0\!: \textsf{Nat}} \quad\quad\quad \dfrac{n\!: \textsf{Nat}}{\textsf{s}\,n\!: \textsf{Nat}} $$This says “(1) $0$ is a natural number, (2) For any natural number $n$, $\mathsf{s\,}n$ is a natural number, and (3) nothing else is a natural number.” So the type of natural numbers is inhabited by $0$, $\mathsf{s\,}0$, $\mathsf{s\,s\,}0$, $\mathsf{s\,s\,s\,}0$, $\mathsf{s\,s\,s\,s\,}0$, and so on. We’ll write these as 0, 1, 2, 3, 4, and so on. These abbreviations should be familiar to you.
Now for the integers:
$$ \dfrac{n\!: \textsf{Nat}}{\textsf{pos}\,n\!: \textsf{Int}} \quad\quad\quad \dfrac{n\!: \textsf{Nat}}{\textsf{neg}\,n\!: \textsf{Int}} $$So the type of integers is inhabited by $\mathsf{pos\,}0$, $\mathsf{neg\,}0$, $\mathsf{pos\,s\,}0$, $\mathsf{neg\,s\,}0$, $\mathsf{pos\,s\,s\,}0$, $\mathsf{neg\,s\,s\,}0$, and so on. We’ll abbreviate these as 0, -0, 1, -1, 2, -2, and so on. But hmmmm, what, then, is the type of 3? We need to figure it out from context, or we can write $3_{\textsf{Nat}}$ or $3_{\textsf{Int}}$ to be explicit.
Here are the rationals:
$$ \dfrac{n\!: \textsf{Int} \quad d\!: \textsf{Nat}}{\textsf{rat}\,n\,d\!: \textsf{Rat}} $$So one-third is $\textsf{rat}\,1\,3$, which we can abbreviate as $\frac{1}{3}$.
We can build lots of numeric types that are useful in programming languages, for example $\textsf{Int8}$, $\textsf{Int16}$, $\textsf{Int32}$, $\textsf{Int64}$, $\textsf{Int128}$, $\textsf{UInt8}$, $\textsf{UInt16}$, $\textsf{UInt32}$, $\textsf{UInt64}$, $\textsf{UInt128}$, $\textsf{Float16}$, $\textsf{Float32}$, $\textsf{Float64}$, $\textsf{Float128}$, $\textsf{Complex64}$, $\textsf{Complex128}$, and so on. Some might require a lot of rules, but they can be defined in principle.
We can make up more types for ourselves. Here is one for primary colors:
$$ \dfrac{}{\textsf{red}\!: \textsf{PrimaryColor}} \quad\quad\quad \dfrac{}{\textsf{green}\!: \textsf{PrimaryColor}} \quad\quad\quad \dfrac{}{\textsf{blue}\!: \textsf{PrimaryColor}} $$You can define the type $\textsf{Unicode}$ whose inhabitants are, you guessed it, the characters of Unicode. That’d be a lot of rules! But it is indeed definable, as there are a finite number of such characters.
Now here is a type for some simple two-dimensional shapes:
$$ \dfrac{r\!: \textsf{Float64}}{\textsf{circle}\,r\!: \textsf{Shape}} \quad\quad\quad \dfrac{w\!: \textsf{Float64}\quad h\!: \textsf{Float64}}{\textsf{rectangle}\,w\,h\!: \textsf{Shape}} \quad\quad\quad \dfrac{a\!: \textsf{Float64}\quad b\!: \textsf{Float64} \quad c\!: \textsf{Float64}}{\textsf{triangle}\,a\,b\,c\!: \textsf{Shape}} $$The idea is that $\mathsf{circle}\,5.0$ is a circle with radius 5.
Now let’s build types from types. If $t_1$ and $t_2$ are types, then $t_1 \times t_2$ is a type, defined like so:
$$ \dfrac{v_1\!: t_1 \quad v_2\!: t_2}{(v_1, v_2)\!: t_1 \times t_2} $$The type $t_1 \times t_2$ is a pair type, which is a special case of a product type, also known as a tuple type. Tuples are not limited to two component types:
$$ \dfrac{v_1\!: t_1 \quad \cdots \quad v_n\!: t_n}{(v_1, \ldots, v_n)\!: t_1 \times \cdots \times t_n} $$Examples: $(2, \mathsf{false}, (\mathsf{true}, \frac{3}{5}))\!: \mathsf{Int \times Bool \times (Bool \times Rat)}$
Can we have a product type with zero components? We can. In fact, there is only one such type. With only one value. The type is called $\textsf{Unit}$:
$$ \dfrac{}{()\!: \textsf{Unit}} $$Next is the type “list of elements of type $t$” which we will write $t^*$:
$$ \dfrac{}{[\,]\!: t^*} \quad\quad\quad \dfrac{x\!: t \quad y\!: t^*}{(x :: y)\!: t^*} $$We will write ${[x]}$ for $(x\,\textbf{::}\,[\,])$, ${[x,y,z]}$ for $(x\,\textbf{::}\,(y\,\textbf{::}\,(z\,\textbf{::}\,[\,])))$, and so on. For an empty list, we would need to rely on context to infer its type, or be explicit by writing, for example, $[\,]_\textsf{Int*}$.
Imagine what the type $\textsf{Unicode}^*$ is. Got it? That’s right! We’ll use the abbreviation $\textsf{String}$ for this type.
Now let’s do “optional of type $t$” which we will write $t\texttt{?}$:
$$ \dfrac{}{\textsf{none}\!: t\texttt{?}} \quad\quad \dfrac{x\!:t}{\textsf{some}\;x\!: t\texttt{?}} $$We thus have $\textsf{some}\:3\!:\mathsf{Nat}\texttt{?}$ and $\textsf{some}\:(-3,T)\!:(\mathsf{Int \times Bool})\texttt{?}$. When writing $\textsf{none}$, we must rely on context to know which type is being referred to, or you can use subscripts to be explicit, e.g., $\mathsf{none_{Int?}}$.
Finally, we'll define the type $\textsf{Void}$ to be the type with no inhabitants. As there are no inhabitants, there are no formation rules.
Don’t confuse Void and UnitThe type $\textsf{Void}$ has no inhabitants at all. The type $\textsf{Unit}$ has a single inhabitant, namely $()$.
Although this shouldn’t be confusing, some programming languages, like Swift, actually call the unit type
Void.Oh well.
Where Behaviors Come From
There’s more to types than just which items inhabit the types. Types have behavior. We capture behavior by defining functions on the types. To define a function, you show how to map each element of one type (the domain) to an element of another type (the codomain). A mapping must exist for each rule that defines the domain type. Here are some examples:
$\begin{array}{l} \textsf{not}\!: \textsf{Bool} \rightarrow \textsf{Bool} \\ \textsf{not}\;\textsf{true} = \textsf{false} \\ \textsf{not}\;\textsf{false} = \textsf{true} \end{array}$
$\begin{array}{l} \textsf{isZero}\!: \textsf{Nat} \rightarrow \textsf{Bool} \\ \textsf{isZero}\;0 = \textsf{true} \\ \textsf{isZero}\;(\textsf{s}\,n) = \textsf{false} \end{array}$
$\begin{array}{l} \textsf{plusTwo}\!: \textsf{Nat} \rightarrow \textsf{Nat} \\ \textsf{plusTwo}\;0 = \textsf{s}\,\textsf{s}\,0 \\ \textsf{plusTwo}\;(\textsf{s}\,n) = \textsf{s}\,\textsf{s}\,\textsf{s}\,n \end{array}$
While definition by cases is the proper way to define functions, we can sometimes use an alternative notation:
$$ \textsf{plusTwo} = \lambda n_{\textsf{Nat}}.\,\textsf{s}\,\textsf{s}\,n $$Did you notice something? Functions are actually values that inhabit function types. Woah. Maybe you noticed this by the way we wrote $\textsf{not}\!: \textsf{Bool} \rightarrow \textsf{Bool}$. Not an accident! $\textsf{Bool} \rightarrow \textsf{Bool}$ is indeed a type. In fact, for any types $t_1$ and $t_2$,
$t_1 \rightarrow t_2$ is a type.
This is good, because let’s try to define the functions $\textsf{and}$ and $\textsf{or}$. So what is $\mathsf{and\,true}$ and $\mathsf{and\,false}$? Well we know we want:
$\begin{array}{l} (\textsf{and}\;\textsf{true})\;\textsf{true} = \textsf{true} \\ (\textsf{and}\;\textsf{true})\;\textsf{false} = \textsf{false} \\ (\textsf{and}\;\textsf{false})\;\textsf{true} = \textsf{false} \\ (\textsf{and}\;\textsf{false})\;\textsf{false} = \textsf{false} \end{array}$
So $\textsf{and true}$ is the function that just produces its argument, and $\textsf{and false}$ is the function that always produces $\textsf{false}$. So we can write:
$\begin{array}{l} \textsf{and}\!: \textsf{Bool} \rightarrow (\textsf{Bool} \rightarrow \textsf{Bool}) \\ \textsf{and}\;\textsf{true} = \lambda x_{\textsf{Bool}}.\,x \\ \textsf{and}\;\textsf{false} = \lambda x_{\textsf{Bool}}.\,\textsf{false} \end{array}$
Here is the function $\textsf{or}$:
$\begin{array}{l} \textsf{or}\!: \textsf{Bool} \rightarrow (\textsf{Bool} \rightarrow \textsf{Bool}) \\ \textsf{or}\;\textsf{true} = \lambda x_{\textsf{Bool}}.\,\textsf{true} \\ \textsf{or}\;\textsf{false} = \lambda x_{\textsf{Bool}}.\,x \end{array}$
Here is an amazing function, known as the conditional. Notice its type. It has a type variable $t$ meaning (at least in this case) that it behaves the same way for all types (meaning you can substitute any real, concrete type for $t$):
$\begin{array}{l} \textsf{cond}\!: \textsf{Bool} \rightarrow (t \rightarrow (t \rightarrow t)) \\ \textsf{cond}\;\textsf{true} = \lambda x_{t}.\,\lambda y_{t}.\,x \\ \textsf{cond}\;\textsf{false} = \lambda x_{t}.\,\lambda y_{t}.\,y \end{array}$
In case that’s hard to read, we can simplify our definition a bit, using fewer $\lambda$ symbols and fewer parentheses:
$\begin{array}{l} \textsf{cond}\!: \textsf{Bool} \rightarrow t \rightarrow t \rightarrow t \\ \textsf{cond}\;\textsf{true}\,x\,y = x \\ \textsf{cond}\;\textsf{false}\,x\,y = y \end{array}$
The convention is that when writing function types, $t_1 \rightarrow t_2 \rightarrow t_3$ is the same as $t_1 \rightarrow (t_2 \rightarrow t_3)$. And when writing function calls, $f\,x\,y$ is the same as $(f\,x)\,y$.
Here is how we add natural numbers:
$\begin{array}{l} \textsf{plus}\!: \textsf{Nat} \rightarrow \textsf{Nat} \rightarrow \textsf{Nat} \\ \textsf{plus}\;0\;m = m \\ \textsf{plus}\;(\textsf{s}\,n)\;m = \textsf{s}\,(\textsf{plus}\;n\;m) \end{array}$
And here is how we multiply natural numbers:
$\begin{array}{l} \textsf{times}\!: \textsf{Nat} \rightarrow \textsf{Nat} \rightarrow \textsf{Nat} \\ \textsf{times}\;0\;m = 0 \\ \textsf{times}\;(\textsf{s}\,n)\;m = \textsf{plus}\;m\;(\textsf{times}\;n\;m) \end{array}$
Ok hold up! It’s time to introduce some notation to make things a bit more familiar. From now on, we’re going to write:
$\begin{array}{lll} \neg b & \text{for} & \textsf{not}\;b \\ a \land b & \text{for} & \textsf{and}\;a\;b \\ a \lor b & \text{for} & \textsf{or}\;a\;b \\ \textsf{if}\;b\;\textsf{then}\;x\;\textsf{else}\;y & \text{for} & \textsf{cond}\;b\;x\;y \\ n + 1 & \text{for} & \textsf{s}\;n \\ n + m & \text{for} & \textsf{plus}\;n\;m \\ n \times m & \text{for} & \textsf{times}\;n\;m \\ \textsf{let}\;x = e\;\textsf{in}\;e' & \text{for} & (\lambda x.\,e')\;e \end{array}$
Relax, these are just abbreviations. The basic low-level notations of our theory still exist.
Back to example function definitions. The length of a list:
$\begin{array}{l} \textsf{length}\!: t^* \rightarrow \textsf{Nat} \\ \textsf{length}\;[\,] = 0 \\ \textsf{length}\;(x\,\textbf{::}\,y) = (\textsf{length}\;y) + 1 \end{array}$
Appending two lists:
$\begin{array}{l} \textsf{append}\!: t^* \rightarrow t^* \rightarrow t^* \\ \textsf{append}\;[\,]\;z = z \\ \textsf{append}\;(x\,\textbf{::}\,y)\;z = x\,\textbf{::}\,(\textsf{append}\;y\;z) \end{array}$
Reversing a list:
$\begin{array}{l} \textsf{reverse}\!: t^* \rightarrow t^* \\ \textsf{reverse}\;[\,] = [\,] \\ \textsf{reverse}\;(x\,\textbf{::}\,y) = \textsf{append}\;(\textsf{reverse}\;y)\;[x] \end{array}$
Mapping a function over a list:
$\begin{array}{l} \textsf{map}\!: (t_1 \rightarrow t_2) \rightarrow t_1^* \rightarrow t_2^* \\ \textsf{map}\;f\;[\,] = [\,] \\ \textsf{map}\;f\;(x\,\textbf{::}\,y) = (f\;x)\,\textbf{::}\,(\textsf{map}\;f\;y) \end{array}$
Filtering a list:
$\begin{array}{l} \textsf{filter}\!: (t \rightarrow \textsf{Bool}) \rightarrow t^* \rightarrow t^* \\ \textsf{filter}\;p\;[\,] = [\,] \\ \textsf{filter}\;p\;(x\,\textbf{::}\,y) = \textsf{if}\;(p\;x)\;\textsf{then}\;(x\,\textbf{::}\,(\textsf{filter}\;p\;y))\;\textsf{else}\;\textsf{filter}\;p\;y \end{array}$
Sometimes it’s helpful to think of an optional as kind of like a sequence of 0 or 1 element. In this case, functions like $\textsf{map}$ make sense to apply to optionals:
$\begin{array}{l} \textsf{map}\!: (t_1 \rightarrow t_2) \rightarrow t_1\texttt{?} \rightarrow t_2\texttt{?} \\ \textsf{map}\;f\;\textsf{none} = \textsf{none} \\ \textsf{map}\;f\;(\textsf{some}\;x) = \textsf{some}\;(f\;x) \end{array}$
This gives us an elegant way to define a function for determining the index of the first occurrence of an element in a list:
$\begin{array}{l} \textsf{indexOf}\!: t \rightarrow t^* \rightarrow \textsf{Nat}\texttt{?} \\ \textsf{indexOf}\;x\;[\,] = \textsf{none} \\ \textsf{indexOf}\;x\;(y\,\textbf{::}\,ys) = \\ \quad \quad \textsf{if}\;x = y\;\textsf{then}\;\textsf{some}\;0\;\textsf{else}\;\textsf{map}\;(\lambda n.\,n+1)\;(\textsf{indexOf}\;x\;ys) \end{array}$
We’ll create example invocations for each of these.
Subtypes
Philosophy question: should a thing inhabit just one type? In some mathematically-oriented theories they do. Pragmatically, though, it makes sense to allow things to be in more than type. Like $3$. Why not let it inhabit $\textsf{Nat}$ and $\textsf{Int}$ and maybe even more numeric types? If we allow this, then we might start to notice that every inhabitant of $\textsf{Nat}$ also inhabits $\textsf{Int}$. That is, $\textsf{Nat}$ is a subtype of $\textsf{Int}$. We write:
$$ \textsf{Nat} \; \texttt{<:} \; \textsf{Int} $$Conversely, $\textsf{Int}$ is a supertype of $\textsf{Nat}$.
Let’s get super technical:
$t_1 \; \texttt{<:} \; t_2$ if and only if for every $v$ such that $v\!: t_1$, we have $v\!: t_2$.
Union and Intersection Types
If we allow individuals to inhabit multiple types, then it makes sense to define union types. The union $t_1 \mid t_2$ is inhabited by exactly all the inhabitants of $t_1$ and those of $t_2$. Yes, it’s possible for $t_1$ and $t_2$ to overlap. So the type $\textsf{Nat} \mid \textsf{Int}$ is just $\textsf{Int}$.
But the type $\textsf{Int} \mid \textsf{String}$ is perhaps interesting. Maybe you can find a use for it?
In case you were wondering, yes, if you have union types, you can also have intersection types, also. We write them like this: $t_1\:\texttt{&}\:t_2$.
- $\textsf{Nat} \mid \textsf{Int}$ is $\textsf{Int}$
- $\textsf{Nat}\:\texttt{&}\:\textsf{Int}$ is $\textsf{Nat}$
- $\textsf{Nat}\:\texttt{&}\:\textsf{String}$ is $\textsf{Void}$
- $\textsf{Void} \mid t$ is $t$
- $\textsf{Void}\:\texttt{&}\:t$ is $\textsf{Void}$
- $t \mid t$ is t
- $t\:\texttt{&}\:t$ is t
Are you getting set theory vibes?Please calm down.
Types are not sets.
TYPES ARE NOT SETS.
We’ll talk about sets later. Please ffs do not let any preconceived notions of sets cloud your learning of the beauty of types. Keep. your. focus. on. types.
Sums, Products, and Exponents
Here are two types, $C$ (for color, with 3 inhabitants $r$, $g$, and $b$) and $D$ (for direction, with 2 inhabitants $l$ and $r$):
$$ \dfrac{}{r\!: C} \quad\quad\quad \dfrac{}{g\!: C} \quad\quad\quad \dfrac{}{b\!: C} $$ $$ \quad\quad\quad \dfrac{}{l\!: D} \quad\quad\quad \dfrac{}{r\!: D} $$The inhabitants of $C \times D$ are:
$$ (r,l),\;(r,r),\;(g,l),\;(g,r),\;(b,l),\;(b,r) $$Did you notice that $C$ has 3 inhabitants and $D$ has 2 inhabitants and $C\times D$ has $3 \times 2 = 6$ inhabitants? See why we call these product types? Right? RIGHT?
Since we have products, maybe we should have sums. We’d like $C + D$ to be a type with $3 + 2 = 5$ inhabitants. You might think a union would work, but wait, it doesn’t because the union ($C \mid D$) only has four elements: $r$, $g$, $b$, and $l$. A true sum type needs to have two distinct $r$'s. We have to tag the “source” of each element of the sum. So the type $C+D$ has these inhabitants:
$$ \mathsf{tag_1}r,\;\mathsf{tag_1}g,\;\mathsf{tag_1}b,\;\mathsf{tag_2}l,\;\mathsf{tag_2}r $$In general, we define a sum type like so:
$$ \dfrac{v_1\!: t_1 \quad \cdots \quad v_n\!: t_n }{\mathsf{tag_1}v\!: t_1 + \cdots + t_n \quad\quad \cdots \quad\quad \mathsf{tag_n}v\!: t_1 + \cdots + t_n} $$If $n = 0$ we have the sum type over no types. It’s the type $\textsf{Void}$ referred to above!
Does this remind you of basic number theory?Void is the empty sum type, the sum of no types, and has zero elements. Just like the number 0 is the sum over a list of no elements, the additive identity.
Unit is the empty product type, the product of no types, and has one element. Just like the number 1 is the product over a list of no elements. The multiplicative identity.
In some theories the void type is actually called $\mathbf{0}$ and the unit type is actually called $\mathsf{1}$.
So, we have sums and products, but what about exponential types? Could there be types $C^D$ and $D^C$? There are, and it’s kind of interesting what they turn out to be. Let’s list all the inhabitants of $C \rightarrow D$:
$$ \begin{array}{llll} (000) & r \mapsto l, & g \mapsto l, & b \mapsto l \\ (001) & r \mapsto l, & g \mapsto l, & b \mapsto r \\ (010) & r \mapsto l, & g \mapsto r, & b \mapsto l \\ (011) & r \mapsto l, & g \mapsto r, & b \mapsto r \\ (100) & r \mapsto r, & g \mapsto l, & b \mapsto l \\ (101) & r \mapsto r, & g \mapsto l, & b \mapsto r \\ (110) & r \mapsto r, & g \mapsto r, & b \mapsto l \\ (111) & r \mapsto r, & g \mapsto r, & b \mapsto r \\ \end{array} $$There are 8 of these, which is not coincidentally $2^3$, exactly the number of inhabitants of $D$ raised to the power of the number of inhabitants of $C$. Therefore, $C \rightarrow D$ is sometimes written $D^C$.
It works the other way, too. $D \rightarrow C$ can be written $C^D$, as it has $3^2 = 9$ inhabitants:
$$ \begin{array}{lll} (00) & l \mapsto r, & r \mapsto r \\ (01) & l \mapsto r, & r \mapsto g \\ (02) & l \mapsto r, & r \mapsto b \\ (10) & l \mapsto g, & r \mapsto r \\ (11) & l \mapsto g, & r \mapsto g \\ (12) & l \mapsto g, & r \mapsto b \\ (20) & l \mapsto b, & r \mapsto r \\ (21) & l \mapsto b, & r \mapsto g \\ (22) & l \mapsto b, & r \mapsto b \\ \end{array} $$And there you have it: function types are the exponential types. 🤯
Sets
If you have a function $A$ of type $t \rightarrow \mathsf{Bool}$, then you can imagine collecting together, in an object, all of the inhabitants $x$ of type $t$ for which $A\,x = \textsf{true}$. That’s a set. That’s what it is.
A lot of people write sets with curly braces.
| Function Notation | Set Notation |
|---|---|
| $\lambda x_{\textsf{Nat}}.\,x=0$ | $\{0\}$ |
| $\lambda x_{\textsf{Nat}}.\,x=2 \vee x=3 \vee x=5$ | $\{2, 3, 5\}$ |
| $\lambda x_{\textsf{Nat}}.\,\textsf{true}$ | $\mathbb{N}$ |
| $\lambda x_{\textsf{Nat}}.\,x > 5$ | $\{ x \in \mathbb{N} \mid x > 5 \}$ |
| $\lambda x_{\textsf{Int}}.\,\textsf{true}$ | $\mathbb{Z}$ |
| $\lambda x_t.\,\texttt{false}$ | $\varnothing$ |
| $(A\,x)_{\textsf{Bool}}$ | $x \in A$ |
There are some theories of mathematics that start with sets. In computer science, theories that begin with types tend to be more useful.
Types in Programming Languages
The way a language defines and uses its types comprises the language’s type system. In defining a type system, a language designer needs to answer questions such as:
- Which are the types of the language?
- Is the set of types fixed, or can you create new ones?
- If a programmer is allowed to create their own types, how do they do so?
- Are types extra-lingual, or are they themselves values?
- If types are values, what kind of types to they have?
- Are the various types classified somehow?
- How do we infer the type of an expression (gets tricky with variables)
- How do we know when two types are exactly the same?
- How do we know when two types are compatible?
- What do we do when expressions are used in a way inconsistent with their type?
Most programming languages have one or more of the following kinds of types:
- Empty Types, which are types that cannot have any values. An empty type is also called a bottom type. In some languages, the bottom type is called
void; in others it is callednever; and still other names may be used. Why the namenever? In programming, we can have functions that never return because they enter an infinite loop or throw an error. boolean, the type containing the values true and false, with operations such as and, or, xor, and not.atom: The type of named symbols. Atoms just have name, and that’s it. You don’t really operate on them (other than testing them for equality perhaps); you just pass them around. They just exist. Some languages call the type of atomssymbol.- Numeric types, with operations such as plus, minus, multiply, divide, remainder, modulo, abs, sign, sin, cos, tan, and on and on and on. Numeric types can be integral, fixed-point, floating point, or complex; bounded or unbounded; signed or unsigned. Examples include:
number,int8,int16,int32,int64,int128,int,uint8,uint16,uint32,uint64,uint128,uint,bigint,fixed,float32,float64,float128,complex64,complex128,ratio,decimal,bigdecimal. char: The type of “characters”, i.e., units of textual information. Exactly what a character is might differ from language to language.- Collection Types, with operations such as size, is_empty, contains, add, remove, retain, clear.
- Set Types, which are unordered collections of unique elements.
- Sequence Types. So many of these, including arrays, lists, stacks, queues, dequeues, priority queues, blocking queues. Even the famous
stringis a kind of sequence, but there’s not a lot of agreement about what exactly strings are sequences of. Are they sequences of bytes? character codes? code points? unicode scalars? graphemes? String types are generally broken. You don't need them. - Mapping Types, types that maps keys to values. If the keys are unique we call them maps or dictionaries; if keys do not have to be unique we call them multimaps. Normally the keys are unordered, but ordered maps exist: these are automatically iterated by in key-order (assuming keys are comparable).
- Singleton types, which are types that only have one value in them. The operations on that individual value vary, of course. Sometimes these are called literal types (in the case where the type name and the value name are the same, as in TypeScript).
- Product Types, The type $T_1 \times T_2$ consists of all pairs $(x, y)$ where $x$ has type $T_1$ and $y$ has type $T_2$. In general you can have products of any size: $T_1 \times T_2 \times \ldots \times T_n$. If $n=0$ you have what’s sometimes called the unit type: the type of only one value, which many languages actually do call
unit. In general, product types are called tuple types. If the components are labeled (named), we get records. - Sum Types. True sum types of the form $T_1 + \ldots + T_n$ are often implemented in languages (such as Swift and Rust) with the
enumkeyword. Occasionally the wordunionmay be employed but this not in agreement with the mainline theory: sums must be tagged and unions are not. If $n=0$ we get the empty type,void.Interestingly, the way types are naturally constructed give rise to sum types. Booleans, numbers, options, and lists, seen at the top of these notes, are essentially sum types. Here are two more:
$$ \dfrac{v\!: t_1}{\textsf{left}\;v\!: \textsf{Either}\;t_1\;t_2} \quad\quad\quad \dfrac{v\!: t_2}{\textsf{right}\;v\!: \textsf{Either}\;t_1\;t_2} $$and
$$ \dfrac{v\!: t_1}{\textsf{success}\;v\!: \textsf{Result}\;t_1\;t_2} \quad\quad\quad \dfrac{v\!: t_2}{\textsf{failure}\;v\!: \textsf{Result}\;t_1\;t_2} $$ - Union Types. These are somewhat rare, but when you see them, they are often implemented with the
|operator, or a construct that actually uses the keywordunion. - Routines, which can be subroutines or coroutines. Operations on routines include invoke and invokeLater. Other terms for invoke include call and apply (from the idea of function “application” — “applying” a function to its argument(s)).
- Function types, computational mappings from arguments to results. We can classify functions in many ways: there are predicates, which return booleans, consumers (also called procedures), that accept arguments but do not return results, suppliers, which take no arguments but return results. In some languages, the number, order, names, and types of parameters are part of the function type.
- Processes, Threads, and Tasks, which are things that run asynchronously. Generally these things send messages to each other, but shared memory is sometimes used. They are generally created with a spawn operation. Internally they use send and receive to communicate.
- The type
type, whose members are...types! If you venture into this world in the context of studying Type Theory and the Foundations of Mathematics, there’s tricky stuff happening around here. But in many programming languages, they just make the typetypeand all is well. But there are other languages that stick close to the theory and deal with universes or kinds as a way of avoiding Girard’s Paradox. You probably haven’t used them before, though. Or have you? - Top types, that contain every single possible value. Again, in theory-land one needs to be really careful about such things. In TypeScript, the top type is
unknown. Other languages call itany(though “any” generally has a completely different meaning in gradually-typed languages, so be careful!)
Let’s attempt a simplification, and show some examples from various languages:
| Kind of Type | Notation | Notes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Empty | $\perp$ | A type with no members at all. A bottom type (meaning it is a subtype of all types). Sometimes called Void. | ||||||||||
| Singleton | $x$ | A type with only a single member. Examples:
| ||||||||||
| Union | $T_1\;|\;T_2\;|\,...|\;T_n$ | A type made up of all the elements of other types. Examples:
| ||||||||||
| Sum | $x_1: T_1 + \ldots + x_n: T_n$ | Similar to a union, but the elements are tagged so we “know where they came from” and there are no overlaps. Also called a Tagged Union or a Discriminated Union. Examples:
| ||||||||||
| Tuple | $T_1 \times \ldots \times T_n$ | The unlabeled product type. Examples:
| ||||||||||
| Record | $(x_1: T_1,..., x_n: T_n)$ | The labeled product type, also known as a Struct. Examples:
| ||||||||||
| Sequence | $T*$ | a.k.a. Array or List. Examples:
| ||||||||||
| Function | $T_1 \rightarrow T_2$ | A function from $T_1$ to $T_2$. Use $\perp$ or a product type for $T_1$ to simulate zero or multiple arguments, and $\perp$ or a product type for $T_2$ to simulate zero or multiple return values. Examples:
| ||||||||||
| Top | $\top$ | All values are a member of this type. The “type of everything.” A top type (meaning all types are a subtype of it). Examples:
|
Singletons and unions give us another way to look at certain types:
- The boolean type is really just
true | falsefor singleton typestrueandfalse. - The character type is the union over all the singleton types for each character in Unicode.
- The string type is just ($\mathsf{Unicode^*}$).
- In some languages, optionals (abbreviated
T?orOptional<T>) are pure unions, such asT | nullfor any typeT; but in others, they are sum types with constructorssomeandnone(as in Rust) orJustandNothing(as in Haskell). - Sequence types end up being $T^* = T \mid (T \times T) \mid (T \times T \times T) \mid \ldots$, but this is kind of weird, so be pragmatic and just use $T^*$.
In case you haven’t seen singleton or union types before, you might not have seen TypeScript.
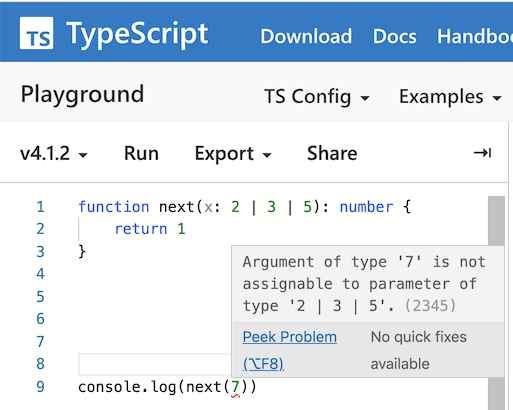
Types have behaviors, too, so they can be classified. One approach is to introduce typeclasses as a means of describing the structure or capabilities of types. Some examples follow:
A type is equatable, or is an eqtype, if values of the type can be tested for equality (==).
- In some languages, all types are equatable because most of the types have reference semantics. In Haskell, however, functions, for example, are not equatable.
A type is comparable (a.k.a. ordered) if values of the type can be compared with < (and often also with <=, >, and >=, and often <=>).
- Generally (at least in the vast majority of languages), if you make your own class, it won’t be comparable be default.
A type is bounded if there is a minimum value of the type and a maximum value of the type.
- Fixed-size integers and simple enumerations are bounded.
A type is showable, or is a showtype if values of the type can be converted to strings.
- Functions and binary streams are generally not showable.
A type is callable if values of its type can be called on, or applied to, other values.
- Functions are callable. In Python, so are types!
A type is enumerable if it has successor and predecessor operations on its values.
- Integers are enumerable, as are characters (enumerated via their code points). Note this definition does not apply to languages with very complex
enumthings, like Swift. Those concepts are completely different.
A type is monoidal, or is a monoid, if it has an associative composition operator, and an identity operator for the composition.
- Concrete example: Functions! They have function composition and the identity
x => x(JS notation). - Abstractly: $\exists e, \bullet:\; \forall a, b, c: a \bullet (b \bullet c) = (a \bullet b) \bullet c \wedge a \bullet e = e \bullet a$
A type is monadic, or is a monad, if values of the type “wrap” underlying values in some way (e.g. optional, list), and there is an operator to wrap a value, and an associative composition operator on functions that unwrap a value and do something to it to produce a new wrapped value, such that the wrapper is an identity for the composition.
Typeclasses in Practice
Languages vary greatly in their treatment of typeclasses. Haskell has a distinguished typeclass concept. Swift implements them via protocols, and other languages just use their own interface or mixin construct.
“Static Types” and “Dynamic Types”
In common, informal speech, a language may have a set of static types and a set of dynamic types. The static types are used at compile-time to look for type-clashes and if found, reject the program as statically illegal. The dynamic types are carried around with each value at run time and are constantly checked every time the value is used.
This leads some people to avoid the use of term “dynamic type” altogether and refer to these things as tags or classifiers or classes.
There are quite a lot of tradeoffs to discuss here. Let’s talk about them.
It’s best here to discuss how specific languages do things, before we can make any general theoretical claims.
- Lua
- All values belong to one of eight and only eight types:
nil,boolean,number,string,function,thread,userdata, andtable. The type of any value is available to you at run time using thetypefunction. All types are dynamic types; there are no static types.When you query for a type at run-time, Lua gives you back a string:
type(3) == 'number' type('hello') == 'string' type({ x=1, y=2 }) == 'table' type(type(3)) == 'string' - Erlang
- There are exactly 11 dynamic types (and no static ones):
atom,integer,float,binary,ref,pid,port,function,list,tuple,map. You can’t ask for the type of an expression, but there are built-in functions to tell you whether or not an expression has a type:is_atom(ten). is_integer($a). is_float(-3.55e-8). is_function(fun (X) -> X*X end). is_reference(make_ref()). is_tuple({dog, "Nika", 5, 'G-SHEP'}). is_list("a string").This is probably a good thing, because as we’ll see, values can have multiple types at the same time. So asking for the type of an expression might be an indication of a type system that is less sophisticated than it could be.
- JavaScript
- Officially there are 8 dynamic types available to you at run time:
Number,BigInt,Boolean,String,Symbol,Null,Undefined, andObject. But it’s more complicated. The built-intypeofoperator can distinguish functions and regexes, andArray.isArraycan tell you if something is an array. When you define your own types via prototypes or theclasssyntax, theconstructorproperty is doing typechecking, too. All types are dynamic types. There are no static types.typeof undefined // 'undefined' typeof 3 // 'number' typeof 3n // 'bigint' typeof true // 'boolean' typeof 'dog' // 'string' typeof(Symbol('dog')) // 'symbol' typeof { x: 1, y: 2 } // 'object' typeof (x => x + 1) // 'function' typeof null // 'object' 😱😱😱😱😱😱😱😱 typeof /a*b/ // 'object' /a*b/.constructor === RegExp // true typeof [1,2,3] // 'object' [1,2,3].constructor === Array // true Array.isArray([1,2,3]) // true class Dog { bark() { return 'woof'; } } class Rat { squeak() { return 'peep'; } } const d = new Dog(); const r = new Rat(); d.constructor // Dog r.constructor // Rat typeof d // 'object' typeof r // 'object' typeof Dog // 'function' typeof Array // 'function' typeof Function // 'function'
- Python
- When asking for the (dynamic) type of an expression in Lua and JavaScript, you get back a string. Python is different—you get back an object, whose type is...
type. And, in fact,typeis a value whose type is... yes,type!type(3) == int type('hello') == str type({ 'x':1, 'y':2 }) == dict type(int) == type type(type) == type type(type(type(type(3)))) == type
Python has a really rich set of dynamic types. But, interestingly, it has static types, too, but they are not checked by Python itself, but only by an external type checker. More on this later.
- TypeScript
- TypeScript’s dynamic types are the same as JavaScript’s, but TypeScript adds dozens of static types. You can even create your own static types.
- OCaml, Haskell, C
- Every type that exists, or that you create, is a static type, and the types are not available to you at all at run time. You can’t do any run-time type checking unless you stick your own type tags on objects programmatically. Languages like this are said to do type erasure, meaning that you had type information before you ran the program (you had your static types for the compiler to use), but the compiled program doesn’t have them anymore—they’ve been erased. There not there anymore. Don’t even think about asking for them, let alone putting them into variables. Why, these languages might say, do you care about types at run time? They’ve already been checked, right? Love your static typing. 🤗
By the way, languages with only static types may actually have a
typeofoperator, but don’t be fooled—this doesn’t do any run-time calcs: the call compiles down into returning the known static type. - C++
- Similar to C in that it wants to erase your static types, except it does add dynamic types when you bring in inheritance. The mechanism is called RTTI.
- Java
- Mostly like C++, but due to a major design flaw, null references are ubiquitous and inescapable for all object types, requiring typechecks for null to happen at runtime. Also, the element type of arrays is carried around at run-time because run-time type checking for arrays is often required. While many consider this a language design flaw, Java’s designers did this on purpose.
int as a value. What problems do you run into?
Okay what have we learned by looking into these specific languages? It appears that most languages distinguish their static and dynamic types, while just a few go all-in on one but not the other. We also learned that the two type systems of a language have really different purposes. And also that they are kind of different things.
Are dynamic types even types?Some folks say typing by its very nature is a static thing. All types are static. Dynamic types aren’t really types, but rather tags that you check at run time. A language that people call “dynamically typed” really just has one giant sum type at compile time: the dynamic “types” are just the tags of the single sum type. This camp would say such a language is unityped (it has just one type).
The other camp says “c’mon we’re all calling these run-time things types so let’s just live with the overloading of the term.”
Make sure to read Bob Harper’s article on unityped languages and this discussion in which the authors of the Julia language defend using “type” even when used at runtime.
So what are we going to do? Let’s just try to be clear. But it will be hard. We might even make mistakes. Consider these notes under construction.
By the way, for a lot of languages, but not all of them, dynamic types aren’t called types at all. They use the word class. Ruby is one of these:
3.class == Integer 'hello'.class == String {x: 1, y: 2}.class == Hash Integer.class == Class Class.class == Class
Java, too, has objects representing classes:
new Integer(3).getClass() // class java.lang.Integer int.class // int "hello".getClass() // class java.lang.String new int[]{1, 2, 3}.getClass() // class [I String.class // class java.lang.String "hi".getClass().getClass() // class java.lang.Class
Here’s a table showing that yes, it’s best to think of classes as dynamic (even if a language can do compile time checks), since class information is usually carried around at run time.
| TYPE | CLASS |
|---|---|
| Is all about behavior | Is about both structure and behavior |
| Is concerned with what objects can do and how they behave | Is a factory for producing objects |
| An object can have many types | An object belongs to exactly one class (the class that created it) |
| Is about interfacing and usage | Is about construction, and things like fields and methods |
| Is considered by many to be exclusively a compile-time concept | Is essentially a run-time tag for run-time type checking |
String, Comparable, and Object. But only one class: String.
String s = "hello"; // "hello" inhabits String Comparable c = s; // "hello" inhabits Comparable Object o = s; // "hello" inhabits Object System.out.println(o.getClass().getName()); // THE class of "hello" is String
In most languages, declaring a class gives rise to a type. The exceptions to this rule are JavaScript and CoffeeScript, where the word class does not make a type: instead it is a funny way of declaring a function and a prototype.
We’re ready to define what a class isA class is (1) an object factory, that is, an entity used for constructing objects. All objects created by a class remember the class that created them at run time; therefore, a class is also (2) a run time classifier tag.
A language may keep track of the class that created an object at compile-time and use it for traditional static type checking.
Terminology may be inconsistentLanguage features like interfaces, sometimes called mixins or protocols, are definitely types rather than classes. You do not use those things for creating objects.
But beware, you may hear Java people saying that an interface is a kind of “class.” Java lingo abuses the notion of class. They are probably talking about “class files.” But in the traditional sense, an interface is not a class, because a class is an object factory.
Type Expressions
In many languages, you get a set of basic types and mechanisms for making new types. Some examples:
| Language | Basic Types | Type formers |
|---|---|---|
| C | ||
| Java | ||
| Standard ML | ||
| Python | ||
| Go | ||
| Rust | ||
| Swift | ||
| Haskell |
Here are some examples from Standard ML:
7 (* int *) (4, "dog") (* int * string *) [5, 3, 2, 7] (* int list *) [ [], [3,3,3], [], [1] ] (* int list list *) [(3, 4.0),(1, 5.5)] (* (int * real) list *) (5, [2.2, 1.0E~4]) (* int * real list *) fn x => x + 8 (* int -> int *) fn x => fn y => x ^ Int.toString(y) (* string -> int -> string *)
But check out this Python script:
print(type([1, 2, 3])) # <class 'list'>
So the run-time type (class) of [1, 2, 3] is list and not “int list.” However, Python does allow a rich set of types for its “type hints” feature, which are annotations meant to aid a static type checker. Interestingly, these types are not part of the language itself, and are completely ignored if the program runs without being checked.
Parameterized Types
In Standard ML, the types int list and string list and ((int * string) -> bool) list are all different. So how do we define functions like length, head, and append, that can work on any list type?
The trick is us type variables. All those types are all instances of the parameterized type 'a list. Lots of languages are like this. Here are some simple examples:
| Language | Example Parameterized Type | Example Instantiated Type | Notes |
|---|---|---|---|
| Standard ML | 'a list | string list | Type variables are 'a, 'b, 'c and so on. If the instantiating type must admit equality, then we write ''a, ''b, ''c, and so on.
|
'a * 'b | string * bool
| ||
'a -> 'b -> 'a | int->(bool*int)->int | ||
| Haskell | [a]a->b | List IntInt->String | Types begin with a capital letter and type variables with a lowercase letter. |
| Java | List<T> | List<String> | |
| Swift | Set<T> | Set<String> |
Type Equivalence
When are two types the same?
typedef struct { int a; int b; } Point; typedef struct { int a; int b; } Pair; Point x; Pair y;
Do x and y have the same type? Should we say “yes” (because they have the same structure), or “no” (because their types have different names, and furthermore appear in different declarations)? These two approaches to determining whether types are the same are structural and named equivalence:
| Structural Equivalence | Name Equivalence |
|---|---|
| Check equivalence by expanding structures all the way down to basic types | Strict: Every type declaration defines a new type |
| Loose: Factor out aliases |
Here is an example from Michael L. Scott:
type alink = pointer to cell;
subtype blink = alink;
p, q : pointer to cell;
r : alink;
s : blink;
t : pointer to cell;
u : alink;
-- If structural: [p q r s t u]
-- If strict name: [p q] [r u] [s] [t]
-- If loose name: [p q] [r s u] [t]
Loose name equivalence is pretty common: we like to distinguish things like Point and Pair above but want the flexibility of aliasing. In Ada we can do both explicitly:
type Height is new Integer; type Weight is new Integer; -- Can’t add heights and weights subtype Height is Integer; subtype Weight is Integer; -- Now you can freely mix them
ML uses structural equivalence:
type pair = int * int; type point = int * int; val x: point = (1, 4); val y: pair = x; type person = {name: string, age: int}; type school = {name: string, age: int}; val p: person = {name="Alice", age=22}; val s: school = p;
But that’s because type does not define a new type! Only a datatype or abstype declaration creates a new type.
abstype person = P of string * int with fun new_person (s, i) = P(s, i) fun name (P(s, i)) = s fun age (P(s, i)) = i end;
Type Compatibility
When can a value of type $S$ be used in a context that expects type $T$?
Possible answers:
- When $S$ and $T$ are equivalent (the same type)
- When $S$ is a subtype of $T$ (where $S$ extends or implements $T$)
- When $T$ is a union type and $S$ is one of the union members
- When $S$ is an intersection type and $T$ is one of the types being intersected
- When $S$ is $S_1\rightarrow S_2$ and $T$ is $T_1\rightarrow T_2$ and a $T_1$ can be used in a $S_1$ context and an $S_2$ can be used in a $T_2$ context 🤯🤔🤨 (THINK ABOUT THIS)
- When an $S$ can be coerced to a $T$
If an $S$ can be used where a $T$ is expected, we say $S$ is compatible with $T$.
By the way, what is coercion? In:
int a;
float b;
float c;
c = a + b;
We may ask whether this is:
- An error, fixable by writing
c = int_to_float(a) + b? - Allowable?
A language that allows this is said to coerce ints to floats, and we say “int is compatible with float”.
- Ada, Modula, ML: no coercion
- Fortran: lots of coercion
- C: lots of coercion in numeric types
- C++: user can define coercions, even accidentally!
Important definitions:
- Type Conversion
- Explicit operation that takes in an object of one type and returns an object of a different type that has the "same value" (not necessarily the same bit pattern).
- Type Coercion
- Implicit
- Non-converting Type Cast
- "Reinterpret" an object as an object of another type by preserving its bit pattern, regardless of value.
class Animal { ... }
class Dog extends Animal { ... }
class Canine = Dog | Wolf
class Famous = Notable & Popular
Then we should be able to assign a:
Dogto anAnimalDogto aCanineNotableto aFamous(Dog)=>Dogto a(Dog)=>Animal(Animal)=>Dogto a(Dog)=>Dog(Animal)=>Dogto a(Animal)=>Animal(Animal)=>Animalto a(Dog)=>Animal
Type Inference
How do we determine the type of an expression?
First thing first: if you have a literal, type inference is obvious. It’s when expressions have variables that things get interesting.
There appear to be four strategies here. Sometimes you can mix and match them.
Manifest Typing Everywhere
Some languages require every variable, every parameter, every return type, every field in a record, and every named entity that can have a type must be declared with an explicit type. C is one such language. Ancient versions of Java, too.
This makes inference rather trivial. Easiest for implementers by far.
Restricted Inference
In Java, Kotlin, Scala, Go, Rust, Swift, and a few others, local variables can have their types inferred provided they have an initializer. But parameters and function return types, while inferrable in some simple cases, often take more work to infer so these languages require manifest typing for these things (except for some small function literals).
scala> var x = 3;
x: Int = 3
scala> var y = x + 3;
y: Int = 6
scala> def f(x) = x + 3;
<console>:1: error: ':' expected but ')' found.
def f(x) = x + 3;
^
scala> def f(x:Int) = x + 3;
f: (x: Int)Int
This is also pretty easy in most cases. Languages that allow this will need to prohibit things like var x = x; of course.
Hindley-Milner
HM is an algorithm for type inference in which you never have to manifest any types (unless you want to.) It looks at all the types of the primitive expressions, then at the types of arguments that the functions and operators expect, and work your way out to the whole expression.
Here’s an example in Standard ML:
(* line 1 *) fun fib (n) =
(* line 2 *) let fun fib_helper (f1, f2, i) =
(* line 3 *) if i = n then f2
(* line 4 *) else fib_helper (f2, f1+f2, i+1)
(* line 5 *) in
(* line 6 *) fib_helper (0, 1, 0)
(* line 7 *) end;
The algorithm will go something like this:
ihas typeint, because it is added to 1 at line 4nhas typeint, because it is compared to i at line 3- all three args at line 6 are
intconstants, and that’s the only use offib_helper(given scope of let), sof1andf2have typeint - also the 3rd arg is consistent with the known
inttype ofi(good!) - and the types of the arguments to the recursive call at line 4 are similarly consistent
- since
fib_helperreturnsf2(known to beint) at line 3, the result of the call at line 6 will have typeint - Since
fibimmediately returns this result as its own result, the return type offibisint
If there’s not enough information to resolve to a known type, ML’s inferencer will bring in type variables. Note how clever it is:
fun I x = x; (* 'a -> 'a *)
fun p x y = y (* 'a -> 'b -> 'b *)
fun first (x, y) = x; (* 'a * 'b -> 'a *)
fun q x = (hd o hd) x; (* 'a list list -> 'a *)
fun c x y = if x = y then "y" else "n"; (* ''a -> ''a -> string *)
In Standard ML, a type variable beginning with two primes can only be instantiated with a type that admits equality.
HM is used in Haskell, Standard ML, OCaml, F#, and other languages.
Read more at Wikipedia.
Control Flow-Assisted Inference
Some languages use control flow to help with type inference. Here is an example from the Rust Book:
fn main() { // Because of the annotation, the compiler knows that `elem` has type u8. let elem = 5u8; // Create an empty vector (a growable array). let mut vec = Vec::new(); // At this point the compiler doesn't know the exact type of `vec`, it // just knows that it's a vector of something (`Vec<_>`). // Insert `elem` in the vector. vec.push(elem); // Aha! Now the compiler knows that `vec` is a vector of `u8`s (`Vec<u8>`) // TODO ^ Try commenting out the `vec.push(elem)` line println!("{:?}", vec); }
Here is a TypeScript example:
function f(x: string | number) { // type of x is string | number here if (typeof x === 'number') { // type of x is number here. } else { // type of x is string here. } }
Type Checking
When is type checking done, and what happens if the checking indicates an expression is used in a manner inconsistent with its type, like trying to compute the age of a string (instead of a person)?
Let’s tackle the “when” question first:
| Static Typing | Dynamic Typing |
|---|---|
| Type checking is done at compile time.
Once a variable’s type is known, it can only be assigned expressions of that type (including related types that can be coerced to it, of course). | Type checking is done at run time.
Because checking is deferred until run-time a variable can be assigned an expression of one type and then later an expression of another type. var x; x = 2; print x + 5; x = "dog"; print concat(x, "house"); |
It is common for languages to have some static typing and some dynamic typing. Stop thinking in binary terms.
Now, what happens if there is a type mismatch?
| Strong Typing | Weak Typing |
|---|---|
Type clashes among unrelated types result in errors. they may be compile time, or even run time (e.g., NoSuchMethodError or ClassCastException) but they are errors. | Type clashes don’t really exist—the language implementation will try to cast the argument into some reasonable (!) type and carry out the operation. |
| Alternate definition: you can’t really circumvent the type system. Example: In Java, even if you explicitly cast a string to an integer, you get an error. | Alternate definition: you can easily circumvent the type system. Example: In C++, you can cast an int* to a void*, then to a char**, and you get away with it.
|
Maybe avoid the terms “strong” and “weak”There are people who get all in a tizzy when they hear the terms “strong typing” and “weak typing.” They don’t think the terms mean very much. Also, the terms are so often muddled and misused. A lot of people say “strong typing” and they don’t even know what they are talking about. For this reason, a lot of people never use the terms at all. Most people would agree, though, that the static/dynamic dimension is a bigger deal.
Remember the term manifest from above?
| Manifest Typing | Implicit Typing |
|---|---|
The types of variables must be given in their declarations.
void f(int x, list<int> z) {
int y = x * x;
z.push_back(y);
}
| The types of variables may be inferred from context.
fun f x z = let y = x * x in z @ [y] endHere x must be an int because of the * operator, so y must be an int as well, and then z must be an int list, and finally f must have type int→int list→int list.
|
Checking code with type variables is done by instantiation. Suppose f has type 'a * int ‑> 'b * 'b ‑> string. Then the following expressions are legal:
f(4, 5)("sd","de")
f(1,1)(2,2)
f([],5)([],[4,4])
but these are not
f(3,2)(4,"p")
f((3,2),5)([5.5,2.2],[1,6])
Languages can be marked according to how far along they are on the various axes:
- Common Lisp: strong, dynamic, implicit
- Ada: strong, static, manifest
- Pascal: strong, almost static, manifest
- Java: strong, some static and some dynamic, manifest
- ML: strong, static, implicit
- JavaScript and Perl: weak, dynamic
- Ruby and Python: strong, dynamic
There’s a real pragmatic concern for manifest typing. Like how to do you specify complex types? Read A comparison of C and Go to see that, um, there are clear ways and no so clear ways.
The literature on strong/weak, static/dynamic, and manifest/implicit typing is enormous, as are the debates and flame wars. Some good reading:
- Mark Jason Dominus on Strong Typing in Perl (awesome presentation, though his definition of “strong typing” is not common)
- Wikipedia articles on data types and type systems
Dependent Types
A dependent type is a type whose definition depends on a value. Examples:- Arrays of length n
- Integers less than 8
- Pairs of integers that sum to 21
Does C++ have dependent types? I mean, you can do:
template <int n> class BoundedList { public: int contents[n]; }
but all types that instantiate this template are created at compile time.
Languages that fully support dynamic dependent types can eliminate many logic errors at compile time! (The type system essentially lets you formulate compile-time proofs that a program will have a certain run time behavior, in terms of the values it will produce.)
Start your study of dependent types at this Stack Overflow question then go to Wikipedia.
Pragmatic Issues
Real programming languages often deal with concerns that we don’t usually mention in theoretical contexts. For example, implementors need to know how to map their language structures to machine structures, and this can lead to some interesting design choices. You can often see machine ideas leaking into language designs.
Numeric Types
To take advantage of hardware registers and arithmetic units, languages often have a variety of numeric types:
- Integers, floats, and ratios (aka rationals) are often distinct
- Integer: Signed or unsigned
- Integer: Saturated or unsaturated
- Integer: Fixed size (8, 16, 32, 64, 128) or unbounded ("BigInt")
- Floats: by size (16, 32, 64, 80, 128)
- Some languages have a particular kind of ratio type called
Decimal
Enumerations
The basic ”enumeration type” is a type with a fixed number of distinct values, ordered from smallest to largest. Typical examples are:
type TrafficLight is (RED, AMBER, GREEN)type Direction is (NORTH, EAST, SOUTH, WEST)
The Boolean type is an enum of the values false and true.
Many languages have a character type which is essentially an enumeration. Each character’s value is its code point.
Sometimes a language will let you loosely interchange a enum value with its integer position in its declaration—or allow you to attach arbitrary (but still distinct) integers to each value in the enum.
Many languages use the term enum to refer to a sum type.
enum for a sum type?
Ranges
Some languages allow you to make types such as:
range(1, 100)range(3, 900, 5)1..1001...1001..<1001..=100
These are just so useful.
Records
Irl, the record type (a tagged product types) goes by many names: record, struct, object, hash, etc. Implementors have to think about how such things are mapped to memory. Things they think about include:
- Whether the order of the fields in memory matters or not
- Memory layout often contiguous, but may have holes for alignment reasons, with some languages giving you explicit control over this (Ada has pragmas for it)
- Compilers may rearrange fields
- When assigning or passing or returning, are copies made?
- Usually you can copy records but not compare them
- Copy can be bitwise, shallow, or deep
Unions and Sums
Perhaps unfortunately, many real languages confuse these terms. We know from above what a union is and what a sum is. But a lot of languages might use the word union for a sum. Sums are often called tagged unions, disjoint unions, or variant records (uggghh). Confusingly, the term enum has become popular for sums. 🤷♀️
Language implementors have to worry about certain things:
- Probably these will be implemented with “overlaying” (Fortran uses
EQUIVALENCE) - Does the language have both unions and sums?
- Actually, if you have classes with inheritance, maybe you don’t need unions or sums at all
- How is the tag stored (for sums)?
- How does the type checker even work with pure (untagged) unions? (What does C do?)
- Speaking of the tags, should you be able to change them?
- Perhaps no, because changing the tag could invalidate the object
- Though perhaps we could prohibit changing just the tag and require a full reassignment (Ada, Algol68)
Sequence Types
Usually in type theory we talk about the type $t^*$ for base type $t$. But in a real language, we are concerned with:
- Lists vs. Arrays
- Stacks, Queues, Deques, Priority Queues, and more
You learned about these in Data Structures.
Arrays
An array is a collection of elements indexed by integers or some other enumerated type, that has constant time access of any element given its index. The elements are almost always packed tightly together in a contiguous memory space. Contrast the array with the list, which needn’t have constant time access, and can be made up of lots of links.
Language designers have a lot of choices when it comes to arrays.
First, there’s the whole idea of bounds:
- Normally, array types are unbounded, but array instances have bounds.
- Is accessing an array outside of its bounds an error? Or does the array object expand to accommodate?
- C doesn’t really have arrays! C “arrays” are just pointers and don’t know about bounds or not. Use at your own risk, and be careful!
- If the bounds are not known at compile time, some kind of indirect storage mechanism is needed, so watch out for shallow vs. deep copy and equality testing.
- Knowing the bounds up front is great! If the bounds are known at compile time, compilers can generate code for element access that uses simple algebraic transforms to pre-compute a lot of the necessary memory access machine code.
Second, the ideas of lifetime and shape matter:
| Static Bounds | Bounds Set at Elaboration | Bounds Can be Changed (Dynamic Shape) |
|
|---|---|---|---|
| Global Lifetime |
C globals | ||
| Local Lifetime |
C locals | Ada locals | |
| Arbitrary Lifetime |
Java | Perl, APL |
Local lifetime / Bounds set at elaboration category is interesting: one can use the alloca syscall to implement
these, giving you automatic deallocation on block exit.
When laying out an array in memory, implementors have choices:
- Column Major
- Row Major (allows 2-D arrays to be the same as arrays of arrays)
- Row Pointers — necessary for ragged arrays, good on machines with small segments.
Slices
Generally, arrays are fixed things. But slices are parts of a (backing) array.
Several languages (Perl, APL, Julia, Fortran 90) have really nice syntaxes for slices. Fortran 90 allows (these examples are from Michael L. Scott):
matrix(3:6, 4:7) columns 3-6, rows 4-7 matrix(6:, 5) columns 6-end, row 5 matrix(:4, 2:8:2) columns 1-4, every other row from 2-8 matrix(:, /2, 5, 9/) all columns, rows 2, 5, and 9
Go and Rust elevate slices to more of a first-class kind of entity. We’ll talk about these in the language-specific course notes for these languages.
Strings
Most (all?) languages have a built-in string type, but variations abound:
- Usually have easy to use literal forms, with escape characters
- May be immutable
- May be interchangeable with character arrays
- If mutable, are usually resizable (except in old Pascal)
- May or may not allow newlines or control characters
- Interpolation may or may not be supported
- Length is ill-defined! (Number of bytes? number of characters? number of code points? number of graphemes?)
- Indexing may also be difficult
- Sometimes a language will have no character type, but will have strings of length 1.
Believe it or not, strings are controversial. Here are some articles:
Sets
Mathematically, a set is an unordered collection of unique elements. In programming languages:
- Usually aren’t built-in but most libraries have them.
- May be mutable or immutable (Python has
setandfrozenset). - Implemented with search trees, tries, hashtables, bitsets, or Bloom filters.
References and Pointers
A reference, or ref, is a value through which you reference another value. They are crucial for modeling sharing of data and for dynamic, linked data structures. Sometimes you will see references called pointers, though technically speaking, a pointer is a reference that you can do arithmetic on. They appear in system languages and low level languages.
Here is a reference to a string value:
The syntax for creating and using references varies from language to language. And when there’s a record being referred to, a lot of languages let you automatically dereference. Given:
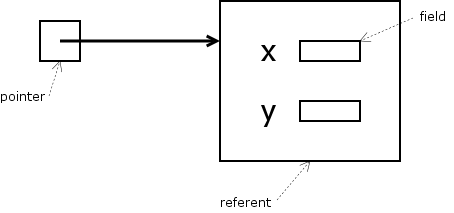
If the pointer is called p (or $p in Perl), then:
| In | the referent is called | and the field is called |
|---|---|---|
| C, C++ | *p | (*p).x or p->x
|
| Ada | p.all | p.all.x or p.x
|
| Pascal, Modula-2 | p^ | p^.x
|
| Java, Python, Ruby, Lua, JavaScript | p (do you know why?) | p.x
|
| Standard ML, OCaml | !p | !p.x
|
| Go, Rust | *p | (*p).x or p.x
|
| Perl | %$p | $$p{x} or $p->{x}
|
If the referent is called v (or %v in Perl), then:
| In | the pointer is called | and the field is called |
|---|---|---|
| C, C++ | &v | v.x
|
| Ada | v'access | v.x
|
| Pascal, Modula-2 | @v | v.x
|
| Java, Python, Ruby, Lua, JavaScript | v (do you know why?) | v.x
|
| Standard ML, OCaml | ref v | — |
| Go, Rust | &v | v.x
|
| Perl | \%v | $v{x}
|
Why are the entries for Java, JavaScript, Python, Lua, Ruby, etc. so weird? It’s because references are often implicit. In Python, for example, every variable (including parameters and attributes) hold references. Every. single. one. Even though the references and referents exist, and you know they exist, you can’t really even distinguish them. It’s so weird.
It is even weirderStandard ML and OCaml have explicit references, but these are only for mutable referents. Most of the other values are implicitly referenced. Oh my.
While it is eventually easy to get used to implicit references, not every language has them. In C++, pointers are explicit:
int x = 5; int* p = &x; int* q = NULL; int* r = new int; int* s = new int[100]; cout << *p << *r << s[20]; cout << *q; // crash
Although references are crucial for modeling certain things, they can be really problematic and disastrous for security. So some languages put in a lot of safeguards. Here are some issues:
- In principle, references can be made to refer to static, stack, or heap-allocated objects.
- Obviously, pointers to stack-allocated objects open up the possibility of dangling references, so:
- Some languages prohibit pointers to stack-allocated objects
- Some languages allow pointers to stack-allocated objects, but only if the object is guaranteed to outlive the pointer
- Some languages allow pointers to stack-allocated objects, but only if the object is guaranteed to outlive the pointer, and the pointer is marked as such
- In Go, when a pointer to a stack-allocated object is known to outlive the object, the object is promoted to the heap
- In languages like C where the programmer explicit allocation and explicit deallocation, it is possible to:
- detach references to heap-allocated objects (memory leak)
- deallocate an objected through a shared pointer (dangling pointer)
- How can we prevent such things?
- Prohibit explicit deallocation and use a garbage collector
- Prohibit explicit deallocation and use reference counting
- Require explicit deallocation to be wrapped in an
unsafeblock - Give programmers some nice tools and conventions, like C++ (this does NOT solve the problem)
- Put in run-time checks to ensure pointers cannot outlive referenced objects (expensive?)
- Put in compile-time checks to ensure pointers cannot outlive referenced objects (a la Rust)
We’ll cover garbage collection separately. For now, you can read Wikipedia’s article on garbage collection, and an interesting developerworks article on Java performance and garbage collection.
Null References
Ah, the billion dollar mistake. We’ve talked about this abomination earlier.
Pointers and Arrays in C
Sometimes, pointers and arrays get conflated in C. After all:
e1[e2]is the same as*(e1 + e2)
For definitions these are completely different things:
int *x; /* is totally different from: */ int x[100]; int *a[n]; /* is totally different from: */ int a[n][100];
But for declarations, at least in parameter declarations, you can blur the distinction:
void f(int* a) { ... }
void g(int b[]) { ... }
An array of ints, or pointer to an int, can be passed to either.
More details in the notes on C.
Streams
The term stream is a bit overloaded. Abstractly, a stream:
- is an object that can be read from and written to, usually sequentially, but sometimes with random access
- is called, if read-only, called a source; if write-only, a sink
- is an excellent abstraction; in practice streams are attached to memory buffers, network connections, database connections, files, pipes, or a variety of similar things
- can be made by pasting two streams together
Sometimes we use the term stream to refer to files.
In Java, streams are their own thing. They work like the streams described above (they are processed sequentially), but are in a pretty large subsystem of their own. See the notes on Java for details.
Regular Expressions
These will be covered later in separate notes.
Functions
Functions are often objects with their own types. We’ll see these later in separate notes on functions.
Processes and Threads
These will be covered later in separate notes on concurrency.
Orthogonality
If a type system is orthogonal, then no type is more special and capable than others. The questions you want to ask to see whether a system is orthogonal or not are whether an object of any type:
- can be represented as a literal?
- can be declared at all?
- can have an initializer?
- can be mutated?
- can be passed as a parameter?
- can be returned from a function?
You might be surprised at how un-orthogonal some language’s type systems are.
A related question is: Are types themselves objects? Various answers to this are:
- They aren’t in JavaScript, C, C++, Erlang, or Elixir.
- Python has a type called
type, so yes there. - Java, Ruby, and many other languages have a class called
Class, so yes there too.
It’s sometimes undesirable, or maybe even impossible, to get true orthogonality, since:
- Expression-oriented languages need an empty or unit type and other languages don’t have these at all.
- First class functions might be difficult to implement or too slow in languages that claim to be fast.
- Some languages allow arrays of anything, other require homogeneous arrays.
- Array indexing really can only be done by discrete types.
- Member, local, and anonymous classes in Java don’t act like top-level ones.
- Blocks of code are often not considered to be objects.
- Simple languages just take short cuts: did you know, in Pascal, you can’t return complex objects from functions?
Type Theory
There is a great deal of theory surrounding our notion of types. Entire books have been written about this theory.
A good place to start on Type Theory is at Wikipedia. The notes you are reading now have focused almost entirely on the more pragmatic issues of types.
You can also read the Type Theory articles in the Stanford Encyclopedia of Philosophy and at nLab. Actually, nLab has a lot of good stuff on type theory and re;ated topics; see for example their articles on Type, Judgment, Proposition, Dependent Type, Type Universe, and Hierarchy of Universes.
More on Mathematics and Philosophy
Many philosophers and mathematicians are interested in a field known as the Foundations of Mathematics. There are three theories that try to be THE foundation: Set Theory (generally the ZFC flavor), Type Theory, and Category Theory. They all work okay and are in some sense equally powerful. See this discussion on Philosophy Stack Exchange and the Wikipedia articles on Intuitionistic Type Theory, Homotopy Type Theory, Curry-Howard Isomorphism, and Foundations of Mathematics.And of course, nLab has its own Foundations of Mathematics article.
More good reads:
Recall Practice
Here are some questions useful for your spaced repetition learning. Many of the answers are not found on this page. Some will have popped up in lecture. Others will require you to do your own research.
- A value’s type constrains the way it may ________________. be used in a program.
- Philosophically, types impose constraints on what we ________________. can and cannot say.
- What are the inhabitants of the type Bool? True and False.
- What are the two constructors of the type Nat? 0 and $\textsf{s}$.
- What are the two rules for defining the type Int? $$\dfrac{n\!: \textsf{Nat}}{\textsf{pos}\,n\!: \textsf{Int}} \quad\quad\quad \dfrac{n\!: \textsf{Nat}}{\textsf{neg}\,n\!: \textsf{Int}}$$
- What does the notation
[2, 3, 5]abbreviate?2::3::5::[] - What is the difference between the types Void and Unit? Void has no inhabitants, Unit has one.
- What is the sole inhabitant of the type Unit? The empty tuple,
(). - What are the inhabitants of $\mathsf{Bool \times Unit}$? Of $\mathsf{Bool + Unit}$? The product type has $2 \times 1 = 2$ inhabitants: $(\mathsf{True, ()})$ and $(\mathsf{False, ()})$. The sum has three inhabitants: $\mathsf{tag_1\,True}, \mathsf{tag_1\,False}$, and $\mathsf{tag_2\,()}$.
- What does it mean for $t_1$ to be a subtype of $t_2$? Every value of type $t_1$ is also a value of type $t_2$.
- How do we write that $t_1$ is a subtype of $t_2$? $t_1\:\texttt{<:}\:t_2$
- How do we write the type that is the union of $t_1$ and $t_2$? $t_1 \mid t_2$
- How do we write the type that is the intersection of $t_1$ and $t_2$? $t_1\:\texttt{&}\:t_2$
- What is the difference between a union type and a sum type? A union type is simply made up of all of the elements of its constituent types. A sum type’s elements are tagged.
- What is the difference between a tuple type and a record type? A tuple type does not have named components, a record type does.
- What is another way to write the type $A \rightarrow B$? $B^A$
- What is a set? In math or programming languages, an unordered collection of unique elements. In type theory, the collection of all values $x$ for which $f\,x = \mathsf{true}$ for some predicate $f$.
- What is a bottom type? A type with no inhabitants.
- What is a top type? A type that is the union of all types in a type system.
- What are the top types of Go, Python, and Ruby, respectively?
interface{},object,BasicObject. - What is a singleton type? A type with exactly one inhabitant.
- How do we write the type of functions from integer lists to the sum of boolean and unit? $\textsf{Int}^* \rightarrow (\textsf{Bool} + \textsf{Unit})$
- How do the optional types of Rust and TypeScript differ? Rust’s
Option<T>is an actual sum type with tagsSomeandNone, while TypeScript uses the pure unionT | null. - What is an eqtype? A comparable type? A bounded type? An eqtype is a type with an equality operator, a comparable type is a type with a less-than operator, and a bounded type is a type with a minimum and maximum value.
- What is a monoid? A set with an associative composition operation and an identity element for the composition.
- What is the difference between a static type and a dynamic type? Static types are used to type check at compile time; dynamic types are available to be checked at run time.
- What is type erasure? The scenario in which there is far less, or the complete absence of, run time type information.
- Why do some people avoid using the term “dynamic typing”? Because dynamic types are essentially just tags attached to values at run time, they are really no different than variants of one giant static type.
- Do Lua and Erlang even have static types? No, they don’t.
- How much type erasure do OCaml and Haskell do? They erase pretty much everything.
- C pretty much performs full type erasure but C++ does not. What is the mechanism for dynamic type checking in C++ called and where is it applied? It is called RTTI and works because C++ class tags are attached to every instance.
- How does one query the type of the expression $e$ at run time in JavaScript? Python? Ruby?
typeof e,type(e),e.class - What are the two things that classes are? (1) object factories, (2) run-time type tags.
- Why do languages like Ruby have a single type
Arraybut in other languages like Java, Rust, and Swift there exist many parameterized array types?Ruby defers type checking of array elements to run-time. Java, Rust, and Swift do much more static typing, so they like to have significantly more type constraints at compile-time. - Type checking is often concerned less with whether two types are identical, but rather when elements of one type T1 can be assigned to an Lvalue constrained to be of type T2. In what situations is this check made? (1) variable initialization, (2) assignment, (3) passing arguments to parameters, (4) returning from a function.
- What are some situations in which a type T1 is compatible with (i.e., used in a context expecting) type T2? There are at least six interesting scenarios, try to give at least three. (1) T1 and T2 are identical, (2) T1 is a subtype of T2, (3) T1 is one of the components of the union type T2, (4) T2 is one of the components of the intersection type T1, (5) each are function types and contravariance is respected for arguments and covariance for return types, and (6) a T2 can be coerced to a T1.
- What is a type conversion? An operation that produces, from an inhabitant of one type $T_1$, an inhabitant of an other type $T_2$ such that the two values are similar.
- What is a type coercion? It is a type conversion that is implicit.
- What is a noncoverting type cast? It is a type conversion that simply reinterprets the bits of a value as an element of another type.
- If Dog is a subtype of Animal, which of the two types, $\mathsf{Dog \rightarrow Animal}$ and $\mathsf{Animal \rightarrow Dog}$, is convertible to the other? The second ($A\rightarrow D$) is convertible to the first ($D \rightarrow A$).
- For which kinds of variables can Java, Kotlin, Scala, Go, Rust, and Swift infer types? Local variables, and sometimes for very simple lambdas, their parameters and return types. (Parameters and return types are not inferred for function declarations.)
- What is the name of the type system used in languages in the ML family that can infer the type of every expression at compile time, even if none are manifest? Hindley-Milner.
- What mainstream languages use control flow to narrow the inferred types of variables? TypeScript and Rust.
- What is the difference between static type checking and dynamic type checking? Static type checking is done at compile time, dynamic type checking is done at run time.
- Although many people claim that the distinction between “strong” and “weak” typing is meaningless, the terms are sometimes applied to situations in which the actual type of an expression does not match what was expected. How are the terms applied to this scenario? Under strong typing, an error is signaled. Under weak typing, a coercion is applied.
- What is manifest typing and what is it contrasted with? Manifest typing is when the type of a variable is explicitly declared. It is contrasted with implicit typing.
- How would most people label the following four languages with the tags Static+Strong, Static+Weak, Dynamic+Strong, or Dynamic+Weak: C, JavaScript, Java, Python? C is Static+Weak, JavaScript is Dynamic+Weak, Java is Static+Strong, and Python is Dynamic+Strong.
- Why is the combination of static typing plus weak arguably typing the worst of the four possible combinations? Many people think that static typing is provides more guarantees than it really does, and might be surprised to find unexpected behavior occur at run time if the coercions from a weakly-typed system are applied after all static type checks pass.
- What is a dependent type? A type that depends on a value.
- How are rational types different from integers or floats? Why are they needed? Rational types are used to represent fractions exactly, without rounding errors.
- What is the difference between an array and a list? An array is a fixed-size collection of elements that can be accessed in constant time. A list is a collection of elements that can be accessed in linear time.
- What are pointers for? Modeling sharing of data and for dynamic, linked data structures.
- What is a memory leak? Usually this term refers to the allocation of memory that becomes inaccessible without ever being deallocated. (It can also me used for memory that is allocated but intentionally never used again.)
- What is a dangling pointer? A pointer that points to a deallocated memory.
- How do C++, Rust, and Swift deal with their lack of tracing garbage collection? They use RAII, ownership types, and ARC, respectively.
- What does it mean for a type system to be orthogonal? Every type is treated the same way.
- Type Theory can be used as a foundation for all of mathematics. What other theories can make this claim? Set Theory and Category Theory.
TODO - MORE QUESTIONS TO COME
Summary
We’ve covered:







