Compiler Architecture

Compilers are programs, and generally very large programs. They almost always have a structure based on the analysis-synthesis model of translation.

Overview

Compilers perform translation. Every non-trivial translation requires analysis and synthesis:

Both analysis and synthesis are made up of internal phases.

Compiler Components

These are the main functional components of a production compiler that looks to generate assembly or machine language (if you are just targeting a high-level language like C, or a virtual machine, you might not have so many phases):

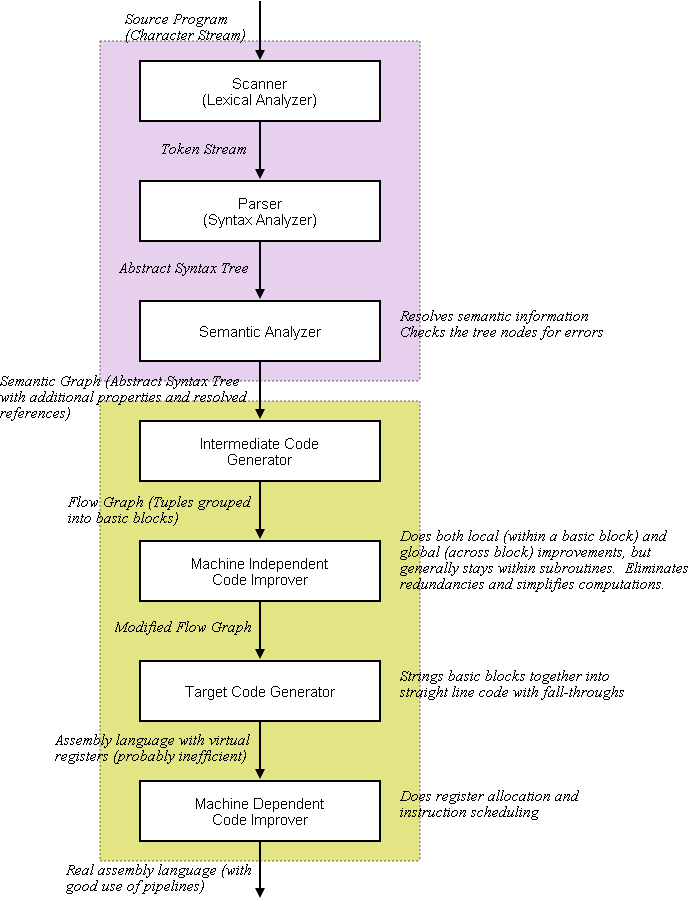
You might also identify an error recovery subsystem and a symbol table manager, too.

Lexical Analysis (Scanning)

The scanner converts the source program’s stream of characters into a stream of tokens. Along the way, it will do things like

Remove comments
Expand macros (in languages like C),
Check indentation and create INDENT and DEDENT tokens, in whitespace-significant languages like Python and Haskell
Remove whitespace (after taking into consideration indents and dedents)

An example in C:

#define ZERO 0
    unsigned  gcd(   unsigned   int  // Euclid’s algorithm
      x,unsigned   y) {   while ( /* hello */  x>   ZERO
   ){unsigned temp=x;x=y   %x;y  = temp ;}return y ;}

gets tokenized into:

unsigned ID(gcd) ( unsigned int ID(x) , unsigned ID(y) ) { while ( ID(x) > INTLIT(0) ) { unsigned ID(temp) = ID(x) ; ID(x) = ID(y) % ID(x) ; ID(y) = ID(temp) ; } return ID(y) ; }

Scanners are concerned with issues such as:

Case sensitivity (or insensitivity)
Whether or not blanks are significant
Whether or not newlines are significant
Whether comments can be nested

Errors that might occur during scanning, called lexical errors include:

Encountering characters that are not in the language’s alphabet
Too many characters in a word or line (yes, such languages do exist!)
An unclosed character or string literal
An end of file within a comment

Syntax Analysis (Parsing)

The parser turns the token sequence into an abstract syntax tree. For the example above, we get this tree:

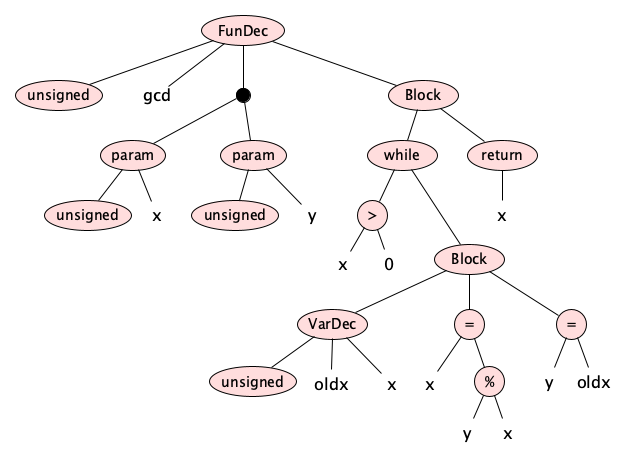
The tree can also be stored as a string

(fundecl unsigned gcd
  (params (param unsigned x) (param unsigned y))
  (block
    (while
      (> x 0)
      (block (vardecl unsigned temp y) (= x (% y x)) (= y temp)))
    (return y)))

Technically, each node in the AST is stored as an object with named fields, many of whose values are themselves nodes in the tree. Note that at this stage in the compilation, the tree is definitely just a tree. There are no cycles.

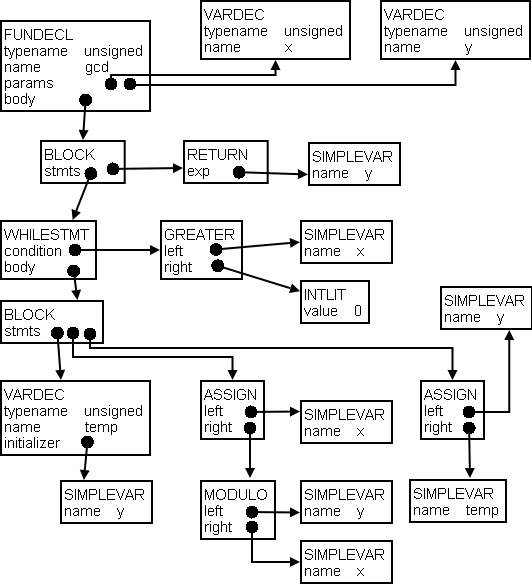
When constructing a parser, one needs to be concerned with grammar complexity (such as whether the grammar is LL or LR), and whether there are any disambiguation rules that might have to be hacked in. Some languages actually require a bit of semantic analysis to parse.

Exercise: Show that the expression (x)-y in C can have two different syntactic interpretations. Hint: Your answer will probably contain the words “subtraction”, “typedef”, “cast”, and “negation”.

Errors that might occur during parsing, called syntax errors include things like following, in C

j = 4 * (6 − x;
i = /5
42 = x * 3

Combining Scanning and Parsing

It is not necessary to actually separate scanning (lexical analysis / tokenization) from parsing (syntax analysis / tree generation). Systems based on PEGs, like Ohm, are actually scannerless: they perform parsing in a predictive fashion, with lexical and syntactic rules mixed together. (However, systems like Ohm will need a pre-parsing phase to handle indents and dedents.)

When using a scannerless system, the language designer and compiler writer still thinks in terms of tokens and phrases, but does not have to worry about complex rules like the so-called Maximal Munch principle. Lookahead captures any kind of tokenization scheme you need. Besides, the predictive nature of scannerless parsing means we never have to decide whether a * is a unary operator pointer dereference token or a binary multiplication operator token or a star token. We always have context when parsing predictively.

Semantic Analysis

During semantic analysis we have to check legality rules and while doing so, we tie up the pieces of the syntax tree (by resolving identifier references, inserting cast operations for implicit coercions, etc.) to form a semantic graph.

Continuing the example above:

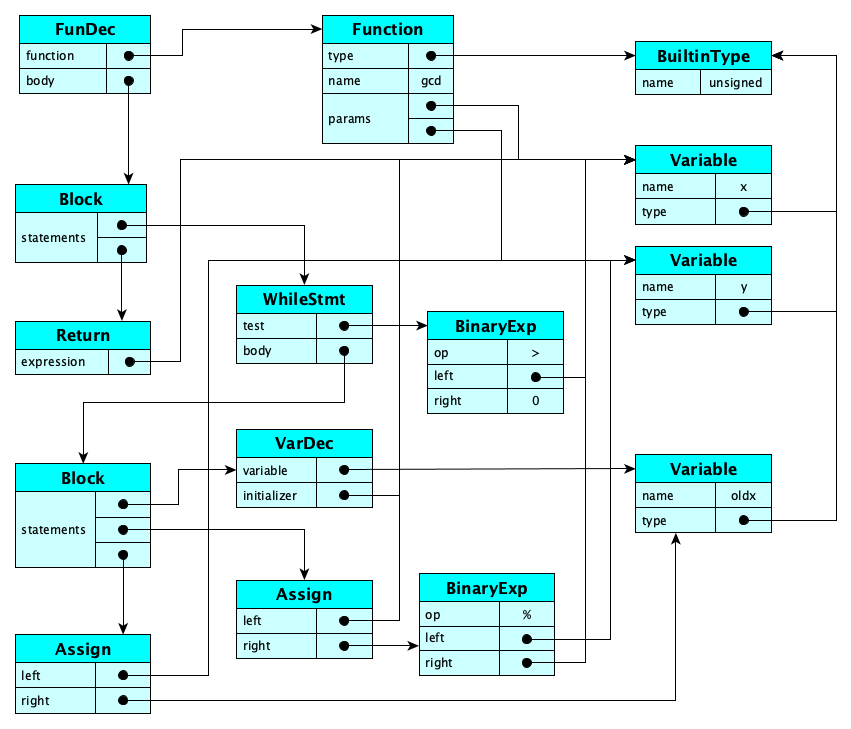
Obviously, the set of legality rules is different for each language. Examples of legality rules you might see in a Java-like language include:

Multiple declarations of a variable within a scope
Referencing a variable before its declaration
Referencing an indentifier that has no declaration
Violating access (public, private, protected, ...) rules
Too many arguments in a method call
Not enough arguments in a method call
Type mismatches (there are tons of these)

Exercise: Give examples of each of the above.

Errors occurring during this phase are called static semantic errors.

Exercise: The language Pascal has an unusual syntax when it comes to expressions: it gives the and operator (which requires boolean operands) higher precedence than relational operators! Show how this implies that the expression x-4<=5 and 2<y is a static semantic error.

Intermediate Code Generation

The intermediate code generator produces a flow graph made up of tuples grouped into basic blocks. For the example above, we’d see:

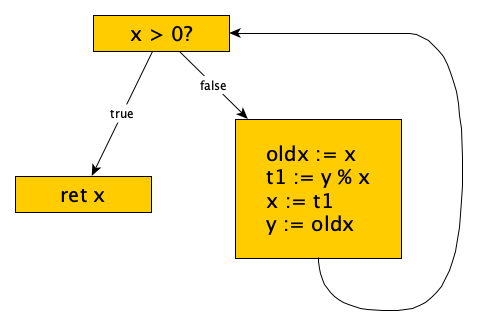
You can read more about intermediate representations elsewhere.

Machine Independent Code Improvement

Code improvement that is done on the semantic graph or on the intermediate code is called machine independent code optimization. In practice there are zillions of known optimzations (er, improvements), but none really apply to our running example.

Code Generation

Code generation produces the actual target code, or something close. This is what I got when assembling with gcc 6.3 targeting the x86-64, without any optimizations:

gcd(unsigned int, unsigned int):
        pushq   %rbp
        movq    %rsp, %rbp
        movl    %edi, -20(%rbp)
        movl    %esi, -24(%rbp)
.L3:
        cmpl    $0, -20(%rbp)
        je      .L2
        movl    -20(%rbp), %eax
        movl    %eax, -4(%rbp)
        movl    -24(%rbp), %eax
        movl    $0, %edx
        divl    -20(%rbp)
        movl    %edx, -20(%rbp)
        movl    -4(%rbp), %eax
        movl    %eax, -24(%rbp)
        jmp     .L3
.L2:
        movl    -24(%rbp), %eax
        popq    %rbp
        ret

Here is code for the ARM, using gcc 5.4, without optimizations:

gcd(unsigned int, unsigned int):
        sub     sp, sp, #32
        str     w0, [sp, 12]
        str     w1, [sp, 8]
.L3:
        ldr     w0, [sp, 12]
        cmp     w0, 0
        beq     .L2
        ldr     w0, [sp, 12]
        str     w0, [sp, 28]
        ldr     w0, [sp, 8]
        ldr     w1, [sp, 12]
        udiv    w2, w0, w1
        ldr     w1, [sp, 12]
        mul     w1, w2, w1
        sub     w0, w0, w1
        str     w0, [sp, 12]
        ldr     w0, [sp, 28]
        str     w0, [sp, 8]
        b       .L3
.L2:
        ldr     w0, [sp, 8]
        add     sp, sp, 32
        ret

And MIPS code with gcc 5.4, also unoptimized:

gcd(unsigned int, unsigned int):
        daddiu  $sp,$sp,-48
        sd      $fp,40($sp)
        move    $fp,$sp
        move    $3,$4
        move    $2,$5
        sll     $3,$3,0
        sw      $3,12($fp)
        sll     $2,$2,0
        sw      $2,8($fp)
.L3:
        lw      $2,12($fp)
        beq     $2,$0,.L2
        nop
        lw      $2,12($fp)
        sw      $2,28($fp)
        lw      $3,8($fp)
        lw      $2,12($fp)
        divu    $0,$3,$2
        teq     $2,$0,7
        mfhi    $2
        sw      $2,12($fp)
        lw      $2,28($fp)
        sw      $2,8($fp)
        b       .L3
        nop
.L2:
        lw      $2,8($fp)
        move    $sp,$fp
        ld      $fp,40($sp)
        daddiu  $sp,$sp,48
        j       $31
        nop

Machine Dependent Code Improvement

Usually the final phase in compilation is cleaning up and improving the target code. For the example above, I got this when setting the optimization level to -O3:

gcd(unsigned int, unsigned int):
        testl   %edi, %edi
        movl    %esi, %eax
        jne     .L3
        jmp     .L7
.L5:
        movl    %edx, %edi
.L3:
        xorl    %edx, %edx
        divl    %edi
        movl    %edi, %eax
        testl   %edx, %edx
        jne     .L5
.L1:
        movl    %edi, %eax
        ret
.L7:
        movl    %esi, %edi
        jmp     .L1

Optimized ARM code:

gcd(unsigned int, unsigned int):
        cbz     w0, .L2
.L3:
        udiv    w2, w1, w0
        msub    w2, w2, w0, w1
        mov     w1, w0
        mov     w0, w2
        cbnz    w2, .L3
.L2:
        mov     w0, w1
        ret

Optimized MIPS code:

gcd(unsigned int, unsigned int):
        bne     $4,$0,.L3
        move    $2,$5
        b       .L11
        nop
.L4:
        move    $4,$3
.L3:
        divu    $0,$2,$4
        teq     $4,$0,7
        mfhi    $3
        bne     $3,$0,.L4
        move    $2,$4
        j       $31
        move    $2,$4
.L11:
        j       $31
        nop